Typically, after we come throughout a graph downside, we’d have to traverse the construction of the given graph or tree to seek out our resolution to the issue. Our downside may be :
- To seek for a specific node within the graph.
- To search out the shortest distance from a node to every other node or to each different node.
- To depend all of the nodes.
- Or there could be extra complicated duties we have to carry out in the best way downside defines us to do it.
However one factor is for positive we have to traverse the graph. Two very well-known strategies of traversing the graph/tree are Breadth-first-search (BFS) and Depth-first-search (DFS) algorithms.
The primary distinction between these two strategies is the best way of exploring nodes throughout our traversal-
- BFS: Tries to discover all of the neighbors it will possibly attain from the present node. It’s going to use a queue knowledge construction.
- DFS: Tries to achieve the farthest node from the present node and are available again (backtrack) to the present node to discover its different neighbors. It will use a stack knowledge construction.
Deciding what to make use of, BFS or DFS?
A lot of the issues could be solved utilizing both BFS or DFS. It received’t make a lot distinction. For instance, take into account a quite simple instance the place we have to depend the entire variety of cities related to one another. The place in a graph nodes signify cities and edges signify roads between cities.
In such an issue, we all know that we have to go to each node in an effort to depend the nodes. So it doesn’t matter if we use BFS or DFS as utilizing any of the methods we can be traversing all the sides and nodes of a graph. So anyway time complexity can be O(E+V) the place E is the entire variety of edges and V is the entire variety of nodes.
However there are issues when we have to determine to both use DFS or BFS for a sooner resolution. And there’s no generalization. It fully relies on the issue definition. It relies on what we’re looking for within the resolution. We have to perceive clearly what our downside needs us to seek out. And the issue may not instantly inform us to make use of BFS or DFS.
Let’s see just a few examples for higher readability.
Examples of selecting DFS over BFS.
Instance 1:
Contemplate an issue the place you might be standing at your home and you’ve got a number of methods to go from your home to a grocery retailer. You’re mentioned that each path you select has one retailer and is situated on the finish of each path. You simply want to achieve any of the shops.
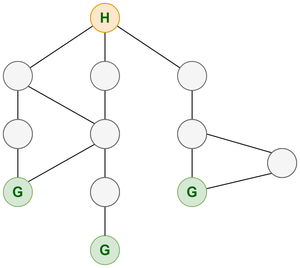
Illustration displaying path from room to grocery retailer
The apparent methodology right here can be to decide on DFS.
As we all know we are able to discover our resolution (grocery retailer) in any of the paths, we are able to simply go on traversing to any neighbor of the present node with out exploring all of the neighbors. There isn’t any want of going by means of BFS as it should unnecessarily discover different paths however we are able to discover our resolution by traversing any of the paths. Additionally, we all know that our resolution is located farthest from the start line so if we select BFS then we should virtually go to all of the nodes as we’re visiting all nodes of a stage and we’ll maintain doing it until the top the place we discover a grocery retailer.
Instance 2:
Contemplate an issue the place you might want to print all of the nodes encountered in any one of many paths ranging from node A to node B within the diagram.
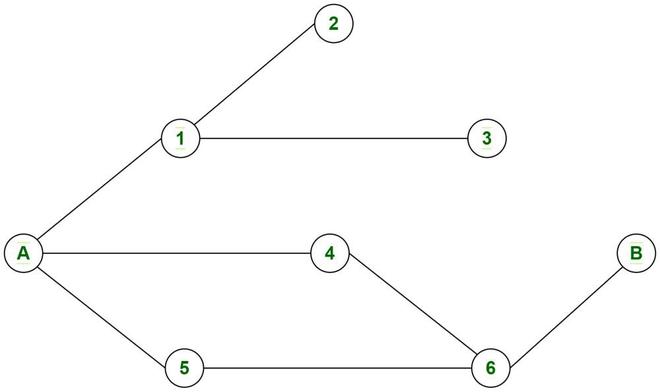
A graph
Right here there are two attainable paths “A -> 4 -> 6 -> B” and “A -> 5 -> 6 -> B”. Right here we require to maintain observe of a single path so there is no such thing as a want of exploring each different path utilizing BFS. Additionally, not each path will lead us from A to B. So we have to backtrack to the present node after which discover one other path and see if that leads us to B. Want for backtracking tells us that we are able to suppose within the DFS path.
Examples of selecting BFS over DFS.
Instance 1:
Contemplate an instance of a graph representing related cities by means of edges. There are just a few nodes coloured in purple that signifies covid affected cities. White-colored nodes point out wholesome cities. You’re requested to seek out out the time the covid virus will take to have an effect on all of the non-affected cities if it takes one unit of time to journey from one metropolis to a different.
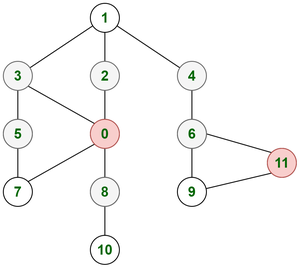
Graph representing above metropolis association
Right here considering of DFS is just not even possible. Right here one affected metropolis will have an effect on all of its neighbors in a single unit of time. That is how we all know that we have to apply BFS as we have to discover all neighbors of the present node first. One other sturdy cause for BFS right here is that each nodes 0 and 11 will begin affecting neighbor cities concurrently. This exhibits we require a parallel operation on each nodes 0 and 11. So we have to begin traversing all of the neighbor nodes of each nodes concurrently. So we are able to push nodes 0 and 11 within the queue and begin traversal parallelly. It’s going to require 2 models of time for all of the cities to get affected.
- At time = 0 models, Affected nodes = {0, 11}
- At time = 1 models, Affected nodes = {0, 11, 3, 2, 8, 7, 6, 9}
- At time = 2 models, Affected nodes = {0, 11, 3, 2, 8, 7, 6, 9, 5, 1, 4, 10}
Instance 2:
Contemplate the identical instance of home and grocery shops talked about within the above part. Suppose now you might want to discover the closest grocery retailer from the home as an alternative of any grocery retailer. Contemplate that every edge is of 1 unit distance. Contemplate the diagram beneath:
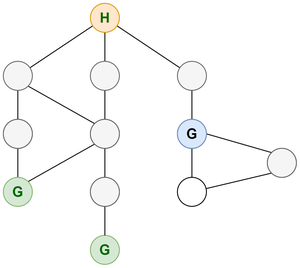
Graph representing grocery retailer
Right here utilizing DFS like earlier is not going to be possible. If we use DFS then we’ll journey down a path until we don’t discover a grocery retailer. However as soon as we now have discovered it we aren’t positive if it’s the grocery retailer on the shortest distance. So we have to backtrack to discover a grocery retailer on different paths and see if every other grocery retailer has a distance lower than the present discovered grocery retailer. It will lead us to go to each node within the graph which isn’t in all probability the easiest way to do it.
We are able to use BFS right here as BFS traverses nodes stage by stage. We first verify all of the nodes at a 1-unit distance from the home. If any of the nodes is a grocery retailer then we are able to cease else we’ll see the following stage i.e all of the nodes at a distance 2-unit from the home and so forth. It will take much less time in most conditions as we is not going to be traversing all of the nodes. For the given graph we’ll solely discover nodes as much as two ranges as on the second stage we’ll discover the grocery retailer and we’ll return the shortest distance to be 2.
Conclusion:
We are able to’t have fastened guidelines for utilizing BFS or DFS. It completely relies on the issue we are attempting to resolve. However we are able to make some basic instinct.
- We’ll favor to make use of BFS after we know that our resolution would possibly lie nearer to the start line or if the graph has higher depths.
- We’ll favor to make use of DFS after we know our resolution would possibly lie farthest from the start line or when the graph has a higher width.
- If we now have a number of beginning factors and the issue requires us to start out traversing all these beginning factors parallelly then we are able to consider BFS as we are able to push all these beginning factors within the queue and begin exploring them first.
- It’s usually a good suggestion to make use of BFS if we have to discover the shortest distance from a node within the unweighted graph.
- We can be utilizing DFS largely in path-finding algorithms to seek out paths between nodes.
Though utilization of BFS or DFS is just not solely restricted to those few issues. You could find extra purposes and utilization of BFS right here and DFS right here.


