
We’ll learn to establish and measure these results in a regression mannequin utilizing appropriate examples.
On this article, we’ll work out easy methods to calculate the partial (or marginal) impact, the primary impact, and the interplay impact of regression variables on the response variable of a regression mannequin. We’ll additionally learn to interpret the coefficients of the regression mannequin by way of the suitable impact.
Let’s start with the partial impact, also called the marginal impact.
In a regression mannequin, the partial impact of a regression variable is the change within the worth of the response variable for each unit change within the regression variable.
Within the language of Calculus, the partial impact is the partial spinoff of the anticipated worth of the response w.r.t. the regression variable of curiosity.
Let’s see three more and more advanced examples of the partial impact.
Contemplate the next linear regression mannequin:

Within the above mannequin, y is the dependent variable, and x_1, x_2 are regression variables. y_i, x_i_1 and x_i_2 are the values equivalent to the the ith commentary, i.e., the ith row of the info set.
β_0 is the intercept. ϵ_i is the error time period that captures the variance in y_i that the mannequin has not been capable of clarify.
Once we match the above mannequin on an information set, we’re estimating the anticipated, i.e. the imply, worth of y_i for some noticed values of x_i_1 and x_i_2. If we apply the Expectation operator E(.) to either side of equation (1), we get the next equation. Discover that the error time period has disappeared since its anticipated worth is zero:

The partial results of x_i_1 and x_i_2 (or generally, x_1 and x_2) on the anticipated worth of y_i are the respective partial derivatives of y_i w.r.t. x_i_1 and x_i_2, as follows:

In case of a linear mannequin containing solely linear phrases, the partial results are merely the respective coefficients. In such a mannequin, the partial results are constants.
Now, let’s make this mannequin a bit advanced by including a quadratic time period and an interplay time period:

This mannequin continues to be a linear mannequin since its linear in its coefficients. Nevertheless, the partial impact of x_i_2 on the anticipated worth of y_i is now not fixed. As a substitute, the impact will depend on the present values of x_i_2 and x_i_1 as follows:

Lastly, let’s take a look at the next nonlinear mannequin containing the exponentiated imply operate. This mannequin is used for modeling the imply operate of a Poisson course of:

On this mannequin, the partial impact of x_i_1 is as follows:

We see that on this case, the change within the anticipated worth of y_i per unit change in x_i_1 isn’t solely not fixed, however it will depend on present worth of each single variable and the worth of all coefficients.
Let’s now flip our consideration to what the most important impact means in a regression mannequin.
In a linear regression mannequin containing solely linear phrases, the most important impact of every regression variable is similar because the partial impact of that variable.
Thus, within the following mannequin that we noticed earlier:

The primary results within the above mannequin are merely β_1 and β_2.
Since this mannequin incorporates solely linear phrases, it’s generally referred to as the most important results mannequin.
The interpretation of most important results turns into fascinating when the mannequin incorporates quadratic, interplay, nonlinear or loglinear phrases.
In fashions of the next form:

The coefficients β_1 and β_2 related to variables x_1 and x_2 can now not be interpreted as the primary results related to these variables. So how are most important results calculated in such fashions?
A technique to take action is to calculate the partial impact of every variable and compute it for every row of the info set. Then take the imply of all such partial results.
As an illustration, within the above mannequin, the partial impact of x_i_1 (or generally x_1) on E(y_i) is calculated as follows:

To calculate the primary impact of x_i_1, we should calculate the above partial impact for every row within the knowledge set and take the typical of all these partial results:

Whereas the above system offers a sound means to calculate the primary impact, it’s an approximation that’s relevant actually solely to the info set in hand. In reality, it’s debatable whether or not the primary impact ought to be calculated in such fashions, or it needs to be merely ignored in case of such fashions that don’t comprise solely linear phrases.
Lastly, let’s overview what is supposed by interplay impact.
Let’s lengthen our linear mannequin by together with an extra time period as follows:

The time period x_i_1*x_i_2 which is the multiplication of the noticed values of the 2 regression variables represents the interplay between the 2 variables. This time, after we take the partial spinoff of the anticipated worth of y_i w.r.t. x_i_1, we get the next:

The change in E(y_i) with respect to x_i_1 is now not simply β_1. As a result of presence of the interplay time period, it’s β_1 plus a amount that will depend on the present worth of x_i_2 occasions the coefficient β_3 of the interplay time period. If the coefficient β_3 occurs to be adverse, it should cut back the web change in y_i for every unit change in x_i_1, and if β_4 is optimistic, it should increase it (assuming x_i_2 is optimistic in each circumstances).
If we take a second spinoff of E(y_i), this time w.r.t. x_i_2, we get the next:

We will now see what the impact of the interplay time period (x_i_1*x_i_2) is on the mannequin.
The coefficient β_3 measures the quantity by which the speed of change of E(y_i) w.r.t. x_i_1 modifications for every unit change in x_i_2. Thus, β_3 measures the diploma of the interplay between x_i_1 and x_i_2.
β_3 is named the interplay impact.
Interpretation of the interplay time period’s coefficient
Simply as with the primary impact, the coefficient of the interplay time period will be interpreted to be the scale of the interplay impact, however solely in a linear mannequin that incorporates solely linear phrases and an interplay time period.
For all different circumstances, and particularly in nonlinear fashions, the coefficient of the interplay time period caries no significance in it’s skill to point the scale of the interplay time period. For example, take into account the next nonlinear mannequin which estimates the imply as an exponentiated linear mixture of regression variables. This mannequin is usually used to signify the non-negative Poisson course of imply in a Poisson regression mannequin:

A primary spinoff of E(y_i) w.r.t. x_i_1 yields the next partial impact of x_i_1 on E(y_i):

Clearly, as in opposition to a linear mannequin with solely linear phrases, within the above partial impact, the coefficient β_3 of x_i_1 now not offers us any clues to the scale of the primary impact of x_i_1.
A second spinoff of E(y_i), this time w.r.t. x_i_2 delivers a good messier state of affairs:

The important thing takeaway is that in a nonlinear mannequin, one mustn’t attempt to ascribe any that means to the coefficient of the interplay impact.
The advantages of including interplay results
One could surprise why one would wish to introduce interplay phrases in a regression mannequin.
Interplay phrases are a helpful machine for representing the impact of 1 regression variable on one other one throughout the identical mannequin. The primary impact measures how delicate the response variable is to modifications within the values of a single regressor, maintaining the values of all different variables fixed (or at their respective imply values). The interplay impact measures how delicate is that this sensitivity of E(y) w.r.t. x, to modifications in one other variable z particularly when z additionally occurs to work together with x.
Listed below are a few examples that illustrate the usage of the interplay impact:
- In a mannequin that research the connection of an individual’s revenue with traits similar to age, intercourse and training, one could wish to know by what quantity does the revenue change for every unit change in training degree, if the particular person occurs to be a feminine versus a male. In different phrases, are females members within the examine seen to have benefited from further instructional any extra (or any much less) than male members, all different issues staying the identical. If we signify the relationships utilizing a linear mannequin of revenue regressed on age, intercourse, training and intercourse*training, the interplay impact is the coefficient of intercourse*training.
- In a mannequin that research the affect of temperature and particulate air inhabitants on rainfall depth, the primary results will measure by how the rainfall quantity modifications for unit modifications in temperature or air air pollution respectively, whereas the interplay impact might measure by what quantity will the change in rainfall w.r.t. a unit change in air pollution degree, will itself change for every unit change in temperature.
In the remainder of the article, we’ll construct a mannequin containing an interplay impact. Particularly, we’ll estimate educational efficiency of scholars in two Portuguese faculties by regressing their efficiency on a set of six variables and one interplay time period. The entire knowledge set will be downloaded from UC Irvine’s machine studying repository web site. A curated subset of the info set through which we now have dropped many of the columns from the unique knowledge set, and coded all binary variables as 0 or 1, is out there for obtain from right here.
Right here’s how a portion of this curated knowledge set seems to be like:

Every row incorporates the check efficiency of a singular pupil. The dependent variable (G1) is their first interval grade in Math and it varies from 0 via 20. We’ll regress grade on a lot of elements and one interplay time period as follows:

Right here, failures is the variety of occasions the scholar failed in previous courses. The worth goes from 0 via 4. It’s right-censored at 4.
schoolsup and famsup are boolean variables indicating whether or not the scholar obtained any further instructional help from their college or from their household respectively. A price of 1 signifies they obtained some help, and 0 signifies they obtained no help.
studytime incorporates the period of time the scholar spent finding out per week. Its worth is intervalized to go from 1 via 4 in increments of 1, the place 1 means < 2 hours, 2 means 2 to five hours, 3 means 5 to 10 hours and 4 means higher than 10 hours.
goout represents the extent to which the scholar hangs out with associates outdoors the home. Its an integer worth starting from 1 via 5 the place 1 means very low extent, and 5 means very excessive extent.
intercourse is a boolean variable (1=Feminine and 0=Male).
We have now additionally included an interplay time period on this mannequin referred to as (failures*intercourse).
If we differentiate G1 w.r.t. intercourse, we get the next partial impact of intercourse on G1:
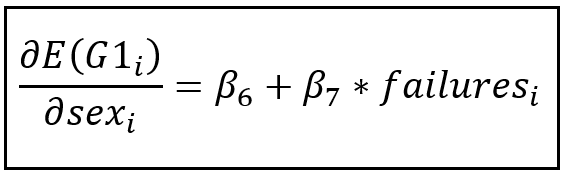
This equation offers us the distinction between the typical grade of female and male college students. As a result of presence of the interplay time period, this distinction can also be depending on the variety of previous failures.
If we differentiate another time, this time w.r.t. failures, we get the next:

β_7 is the speed at which the distinction between the typical grade of female and male college students modifications for every unit change in variety of previous failures.
Thus β_7 estimates the interplay impact between intercourse and variety of failures.
Let’s construct and prepare this mannequin on the info set. We’ll use Python and the Pandas knowledge evaluation library and the statsmodels statistical fashions library.
Let’s begin by importing all of the required packages.
import pandas as pd
from patsy import dmatrices
import statsmodels.api as sm
Subsequent, we’ll use Pandas to load the info set right into a Pandas DataFrame:
df = pd.read_csv('uciml_portuguese_students_math_performance_subset.csv', header=0)
We’ll now type the regression expression in Patsy syntax. We don’t must explicitly specify the intercept. Patsy will routinely add it to the X matrix in a following step.
reg_exp = 'G1 ~ failures + schoolsup + famsup + studytime + goout + intercourse + I(failures*intercourse)'
Let’s carve out the X and y matrices:
y_train, X_train = dmatrices(reg_exp, df, return_type='dataframe')
Right here is how the carved out design matrices seem like:


Discover that Patsy has added a placeholder column in X for the intercept β_0, and it has additionally added the column containing the interplay time period failures*intercourse.
We’ll now construct and prepare the mannequin on (y_train, X_train):
olsr_model = sm.OLS(endog=y_train, exog=X_train)olsr_model_results = olsr_model.match()
Let’s additionally print the coaching abstract:
print(olsr_model_results.abstract())
We see the next output (I’ve highlighted just a few fascinating components):

Find out how to interpret the regression mannequin’s coaching efficiency
The adjusted R-squared is 0.210 implying that the mannequin has been capable of clarify 21% of the variance within the G1 rating. The F-statistic of the F-test is 15.96 and it’s important at a p worth of < .001, that means that the mannequin’s variables are collectively extremely important. The mannequin is ready to do a significantly better job of explaining the variance in pupil efficiency than a easy imply mannequin.
Subsequent, let’s notice that the majority coefficients are statistically important at a p worth of < .05 or decrease. famsup is important at a p of .061 and the interplay time period failures*intercourse is important at a p of .073.
The equation of the fitted mannequin is as follows:

Interpretation of coefficients
Let’s see easy methods to interpret the assorted coefficients of the fitted mannequin.
The partial impact of failures on G1 is given by the next equation:

The coefficient of failures is -1.7986. As a result of presence of the interplay time period (failures*intercourse) , -1.7986 is now not the primary impact of previous failures on the anticipated G1 rating. In reality, one mustn’t ascribe any that means to the worth of this coefficient besides within the state of affairs the place the coefficient of intercourse is 0, which it isn’t on this case. One of the best we will do is to calculate the partial impact of failures on E(G1) for every row within the knowledge set and take into account the typical of all these values as the primary impact of failures on E(G1). As talked about earlier, this technique is of doubtful worth and a safer method can be to altogether abandon the pursuit of computing the primary impact of failures, given the presence of the interplay time period.
Precisely identical set of issues maintain whereas deciphering the coefficient of intercourse within the coaching output.
The issues change dramatically whereas deciphering the coefficients of schoolsup, famsup, studytime and goout. None of those variables are concerned within the interplay time period (failures*intercourse) resulting in an easy interpretation of their coefficients as follows.
Throughout all college students, the estimated imply discount of their G1 rating for every unit improve within the period of time they spend in “going out” (goout) is .3105. That is partial impact of goout on E(G1). It’s also the primary impact of goout on E(G1).
Equally, the coefficients of the boolean variables schoolsup and famsup are the respective partial results of that variable on E(G1), and they’re additionally the respective most important impact of that variable on E(G1). Surprisingly, each coefficients are adverse, indicating that college students who obtained further help from their college or their household did on common worse than those that didn’t obtain help. One strategy to clarify this result’s to theorize that many of the college students who’re receiving further help are receiving them as a result of they’re faring poorly of their math grades.
Alternatively, studytime has an unsurprisingly optimistic relationship with the G1 rating with every unit improve in studytime resulting in a rise within the G1 rating by 0.5848.
Lastly, let’s look at the interplay impact of failures with intercourse. The coefficient of the interplay time period (failures*intercourse) is optimistic indicating that for every unit improve in variety of previous failures skilled by the scholar, the sting that male college students appear to have over feminine college students within the G1 rating quickly evaporates, decreasing because it does by 0.7312 factors. This conclusion is borne out by taking the spinoff of E(G1) w.r.t. intercourse which supplies us the partial impact of intercourse on the imply G1 rating:

From the equation, we will see that the partial impact reverse signal in a short time with improve in variety of previous failures:

The next desk and graph reveals one other view (an empirical view) into the identical state of affairs. It reveals the imply scores of feminine and male college students calculated from the info set, for every worth of previous failures:
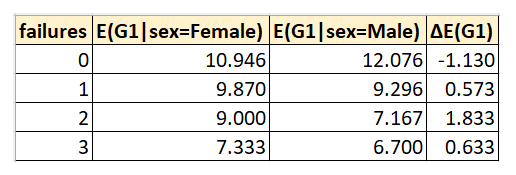
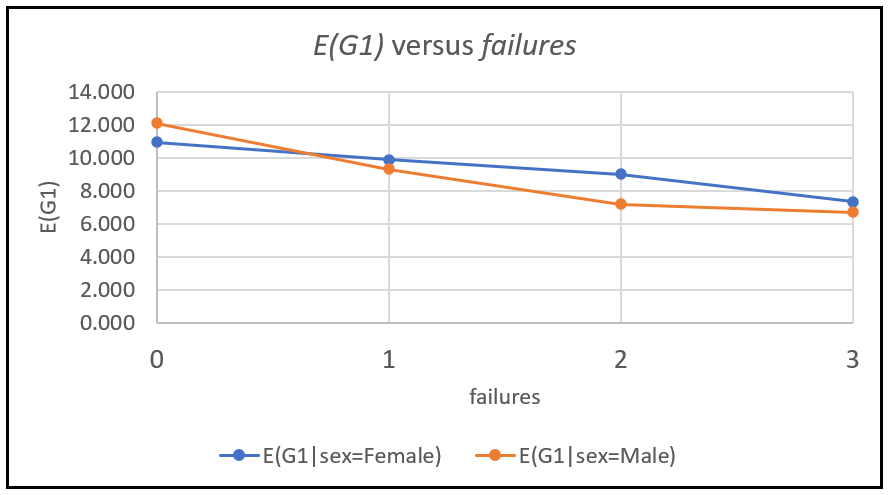
As anticipated, we see the empirical final result agrees with the modeled final result i.e. the one utilizing the equation for the partial impact of intercourse of E(G1). The distinction between female and male college students’ G1 rating shortly reverses with improve in variety of previous failures. Larger ranges of previous failures appear to adversely affecting male college students’ scores rather more than they do feminine college students’ scores. The explanations behind this impact could be rooted in a number of the different elements within the mannequin, or they could be unobserved results which have leaked into the error time period of the mannequin.
Observations of this type are doable by way of the inclusion of interplay phrases. We might not have been capable of simply spot this sample by together with solely the primary results for intercourse and failures within the regression mannequin.
- In a regression mannequin, the partial impact or marginal impact of a regression variable is the change within the worth of the response variable for each unit change within the regression variable.
- In a linear mannequin that incorporates solely linear phrases, i.e. no quadratic, log, and different kinds of nonlinear phrases, the most important impact of every regression variable is similar as its partial impact.
- For all different fashions, the most important impact of variable will be calculated by averaging the partial impact of the variable over your entire knowledge set. That is at finest an approximation that’s relevant basically solely to the info set in hand. And subsequently, some practitioners desire to altogether ignore the primary results in such sorts of fashions.
- Interplay phrases assist the modeler estimate the impact of 1 regression variable on different variables within the mannequin of their joint skill to clarify the variance within the response variable.
- In sure easy linear fashions, the coefficient of the interplay time period can be utilized to estimate the scale of the interplay impact. Nevertheless, in most fashions, one mustn’t ascribe any that means to the coefficient of the interplay time period.
Information set
Information set of pupil efficiency sourced from UCI Machine Studying Repository below their quotation coverage.
Dua, D. and Graff, C. (2019). UCI Machine Studying Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: College of California, College of Data and Pc Science.
The curated model of the info set used on this article is accessible for obtain from right here.
Paper
P. Cortez and A. Silva. Utilizing Information Mining to Predict Secondary College Pupil Efficiency. In A. Brito and J. Teixeira Eds., Proceedings of fifth FUture BUsiness TEChnology Convention (FUBUTEC 2008) pp. 5–12, Porto, Portugal, April, 2008, EUROSIS, ISBN 978–9077381–39–7.
[Web Link]
Pictures
All photos on this article are copyright Sachin Date below CC-BY-NC-SA, except a unique supply and copyright are talked about beneath the picture.
Should you appreciated this text, please comply with me at Sachin Date to obtain suggestions, how-tos and programming recommendation on subjects dedicated to regression, time sequence evaluation, and forecasting.


