In my earlier posts within the “time sequence for scikit-learn folks” sequence, I mentioned how one can practice a machine studying mannequin to predict the following ingredient in a time sequence. Typically, one might wish to predict the worth of the time sequence additional sooner or later. In these posts, I gave two strategies to perform this. One methodology is to coach the machine studying mannequin to particularly predict that time sooner or later. This methodology is poor as a result of, if one want to know the worth of the time sequence at two totally different factors sooner or later, then they’re once more out of luck.
The opposite methodology is recursive forecasting. That is completed by feeding within the prediction of the mannequin as a brand new enter and utilizing this to foretell a brand new output. One iterates this, “rolling” the predictions ahead till the longer term focal point is reached. In python, this may appear to be
def recursive_forecast(mannequin, input_data, num_points_in_future):
for level in vary(num_points_in_future):
prediction = mannequin.predict(input_data)
# Append prediction to the enter information
input_data = np.hstack((input_data, prediction))
return prediction
From a machine studying viewpoint, this type of forecasting is weird. You might practice a mannequin that has wonderful check error on predicting the following step in a time sequence however then fails spectacularly to forecast a number of values within the time sequence. In case your true goal is to reduce error on predicting a number of future values in a time sequence, then you definitely should assemble a loss perform that instantly minimizes this error! On this weblog submit I’ll present you a pair other ways to do that so-called direct forecasting utilizing my library skits. Alongside the best way, we can have some enjoyable shifting up the chain of mannequin complexity, from scikit-learn linear fashions, to XGBoost, to deep studying fashions in PyTorch. And naturally, all the pieces will likely be suitable with the scikit-learn API.
Observe: Whereas recursive forecasts could appear loopy from a machine studying standpoint, there are various strong causes to make use of them, and the query of whether or not to make use of recursive or direct forecasts is pretty nuanced. Souhaib Ben Taieb’s PhD thesis (pdf) has a superb dialogue with references.
When unsure, use extra fashions
If compute and reminiscence and time are low cost, then you may brute pressure a forecast by coaching a separate mannequin for every level sooner or later that you just wish to predict. For instance, if in case you have a time sequence with a pattern each minute (aka a sampling frequency of 1/60 Hz) and also you want to forecast each level within the subsequent hour, then you definitely would practice 60 totally different fashions. Every mannequin would have a distinct level sooner or later as its “goal” (or y in scikit-learn parlance), and you’d generate a full hour forecast by calculating the prediction of every mannequin.
The good factor about this methodology is that you should use any regression mannequin you need that predicts a single goal. And in reality, it seems that scikit-learn has a category that means that you can do that. All it’s important to do is wrap your mannequin estimator with the MultiOutputRegressor class. As soon as wrapped, then scikit-learn will practice a person estimator for every column in your y matrix. Thus, all we have to do is rework our time sequence y such that it turns from an array right into a matrix the place every column is a step ahead sooner or later. The HorizonTransformer in skits does simply this. For a horizon of 3, a time sequence goes from
import numpy as np
y = np.arange(10, dtype=np.float32)
y
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.], dtype=float32)
from skits.preprocessing import HorizonTransformer
ht = HorizonTransformer(horizon=3)
y_horizon = ht.fit_transform(y.reshape(-1, 1))
y_horizon
array([[ 0., 1., 2.],
[ 1., 2., 3.],
[ 2., 3., 4.],
[ 3., 4., 5.],
[ 4., 5., 6.],
[ 5., 6., 7.],
[ 6., 7., 8.],
[nan, nan, nan],
[nan, nan, nan],
[nan, nan, nan]], dtype=float32)
Observe that the HorizonTransformer maintains the size of the y array, so we find yourself with NaN values for the final 3 rows.
Begin Easy: Linear Fashions
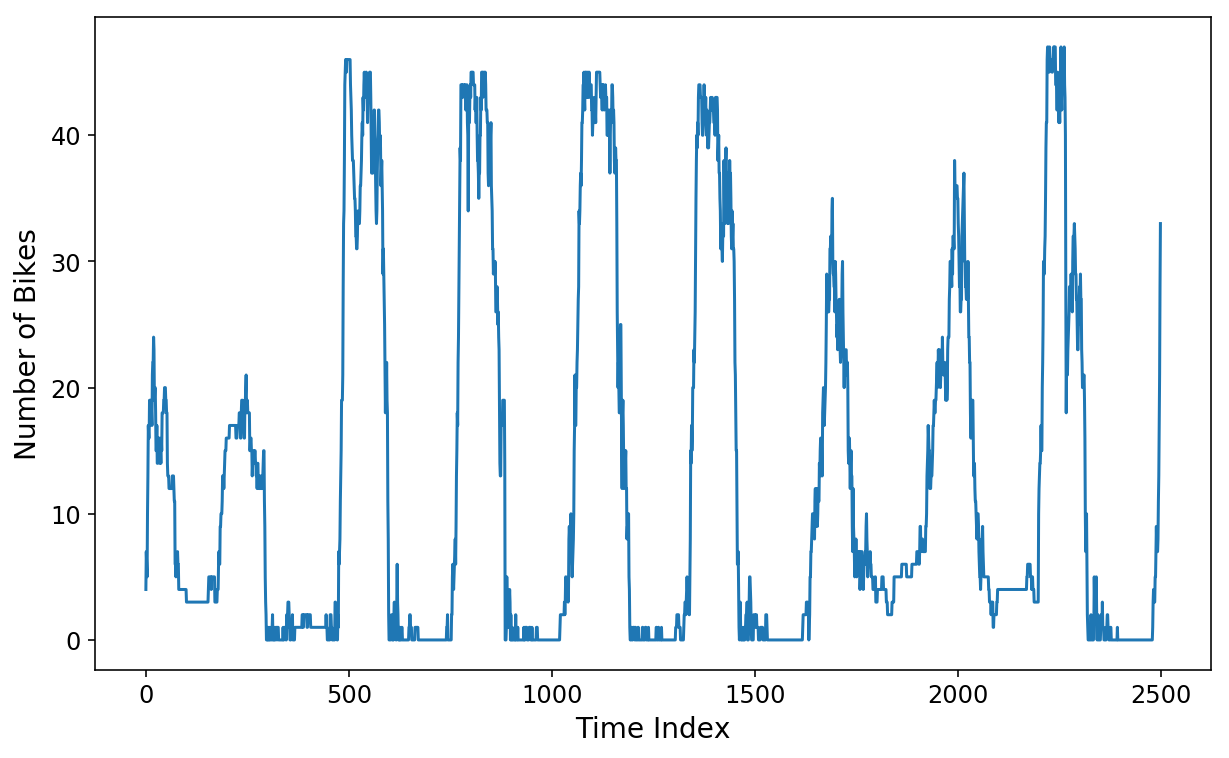
Let’s now attempt coaching a linear regression mannequin to foretell the following 2 hours of information on our good ol’ Citibike dataset that I’ve been utilizing all through this sequence. Recall that the info consists of the variety of bikes that had been out there on the Citibike station close to my house. The factors within the time sequence are spaced aside by 5 minutes. Thus, if we wish to predict the following 2 hours of information, then we might want to predict the following 24 factors within the time sequence.
%config InlineBackend.figure_format = 'retina'
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.ion()
mpl.rcParams['figure.figsize'] = (10, 6)
mpl.rcParams['figure.titlesize'] = 16
mpl.rcParams['axes.labelsize'] = 14
mpl.rcParams['axes.titlesize'] = 16
mpl.rcParams['legend.fontsize'] = 14
mpl.rcParams['xtick.labelsize'] = 12
mpl.rcParams['ytick.labelsize'] = 12
import pickle
with open('station_496_availability.pkl', 'rb') as f:
y = pickle.load(f)
plt.plot(y[:2500]);
plt.xlabel('Time Index');
plt.ylabel('Variety of Bikes');
We’ll use skits to assemble a design matrix consisting of the earlier week’s value of information. That is positively overkill, however I’ll wish to throw plenty of options on the extra advanced fashions that we’ll construct in a while.
period_minutes = 5
samples_per_hour = int(60 / period_minutes)
samples_per_day = int(24 * samples_per_hour)
samples_per_week = int(7 * samples_per_day)
print(f'Variety of "options": {samples_per_week}')
Variety of "options": 2016
from sklearn.linear_model import LinearRegression
from sklearn.multioutput import MultiOutputRegressor
from sklearn.pipeline import FeatureUnion
from skits.feature_extraction import AutoregressiveTransformer
from skits.pipeline import ForecasterPipeline
from skits.preprocessing import ReversibleImputer
lin_pipeline = ForecasterPipeline([
# Convert the `y` target into a horizon
('pre_horizon', HorizonTransformer(horizon=samples_per_hour * 2)),
('pre_reversible_imputer', ReversibleImputer(y_only=True)),
('features', FeatureUnion([
# Generate a week's worth of autoregressive features
('ar_features', AutoregressiveTransformer(num_lags=samples_per_week)),
])),
('post_feature_imputer', ReversibleImputer()),
('regressor', MultiOutputRegressor(LinearRegression(fit_intercept=False),
n_jobs=6))
])
We now have a pipeline that can generate every week’s value of autoregressive options and match a LinearRegression mannequin for every of the 24 factors within the 2-hour horizon that we want to predict. We’ll reserve 1000 factors on the finish of the time sequence as our “check” information, though this isn’t meant to characterize a real practice/check/cross validation process.
X = y.reshape(-1, 1).copy()
test_size = 1000
train_size = len(X) - test_size
lin_pipeline = lin_pipeline.match(X[:train_size], y[:train_size])
Prediction Inspection
With the fitted pipeline, we will now generate horizon predictions. Calling predict on the pipeline will now generate a 2-hour, 24 information level prediction at every level within the information X. Passing in start_idx will return predictions beginning on the start_idx of X (which in our case would be the begin of the check information).
prediction can have 24 columns the place the primary column represents the primary information level sooner or later (in our case, 5 minutes sooner or later) all the best way as much as the twenty fourth information level sooner or later.
lin_prediction = lin_pipeline.predict(X, start_idx=train_size)
print(f'X form: {X.form}')
print(f'prediction form: {lin_prediction.form}')
X form: (74389, 1)
prediction form: (1000, 24)
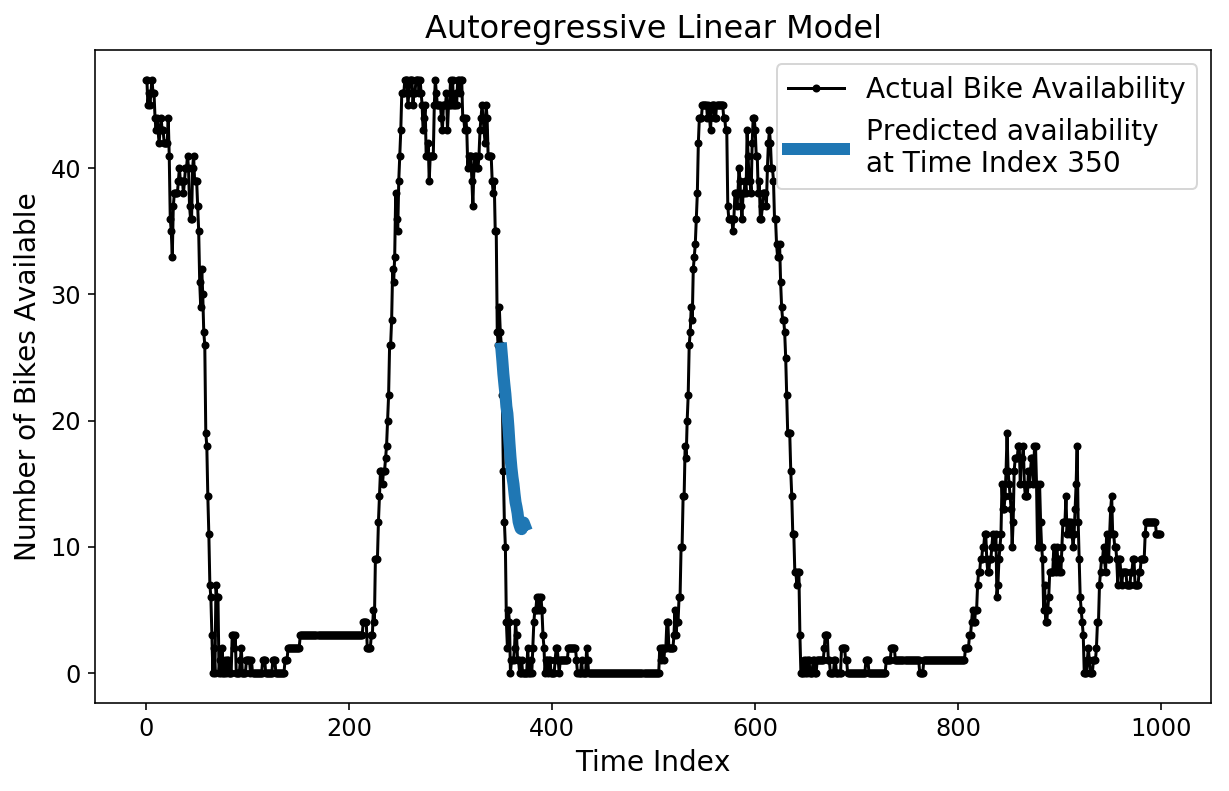
There are a pair totally different ways in which we will now examine our prediction. To start out, we will plot a single, 2-hour prediction towards the bottom fact check information.
plt.determine();
plt.plot(y[-test_size:], 'ok.-');
plt.plot(np.arange(350, 374), lin_prediction[350, :], linewidth=6);
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive Linear Mannequin');
plt.legend(['Actual Bike Availability',
'Predicted availability nat Time Index 350']);
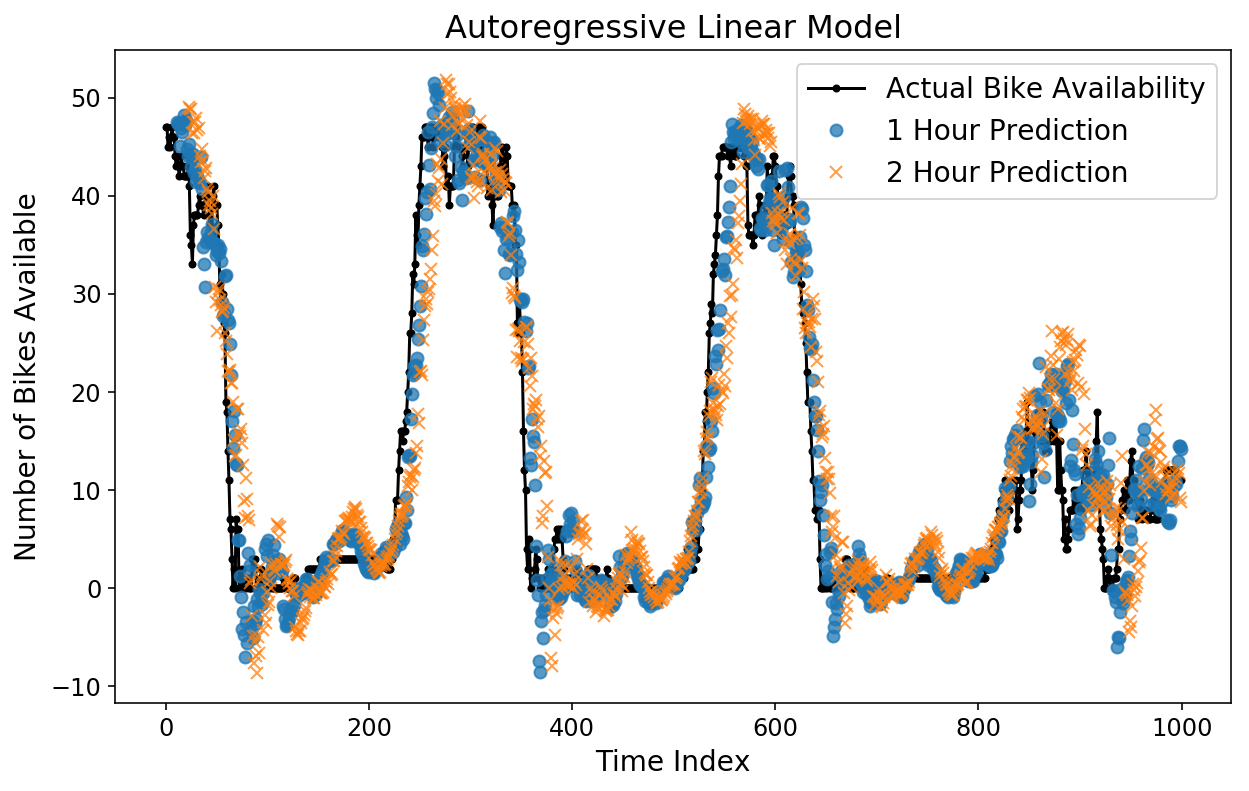
We are able to additionally layer on totally different horizon predictions to see how they examine to one another. Under, I plot the true bike availability, the 1-hour prediction, and the 2-hour prediction. The 1-hour prediction corresponds to what our mannequin would predict for the bike availability at a specific time, given the entire information up till an hour previous to that point.
Surpisingly to me, each the 1-hour and 2-hour predictions look fairly good by eye! You may see that the 2-hour prediction is barely extra “off” from the Precise information in comparison with the 1-hour prediction, which is smart.
plt.determine();
plt.plot(y[-test_size:], 'ok.-');
plt.plot(np.arange(11, test_size), lin_prediction[:-11, 11], 'o', alpha=0.75);
plt.plot(np.arange(23, test_size), lin_prediction[:-23, 23], 'x', alpha=0.75);
plt.legend(['Actual Bike Availability',
'1 Hour Prediction',
'2 Hour Prediction']);
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive Linear Mannequin');
Gazing graphs is useful for instinct however not notably rigorous by way of evaluating true efficiency. We are able to make use of a easy efficiency metric and calculate the imply absolute error (MAE) as a perform of every level sooner or later that we try to estimate. Fortunately, scikit-learn has built-in features that deal with this for 2D y information.
By the best way, why imply absolute error? For one thing like bike availability, it feels pure to need to have the ability to reply the query “What number of bikes off may we be after we predict the bike availability in 1 hour?”
from sklearn.metrics import mean_absolute_error
y_actual = lin_pipeline.transform_y(X)
lin_mae = mean_absolute_error(y_actual[-test_size:], lin_prediction,
multioutput='raw_values')
plt.plot(np.arange(1, 25) * 5, lin_mae);
plt.xlabel('Minutes within the Future');
plt.ylabel('Imply Absolute Error');
plt.title('Autoregressive Linear Mannequin MAE');
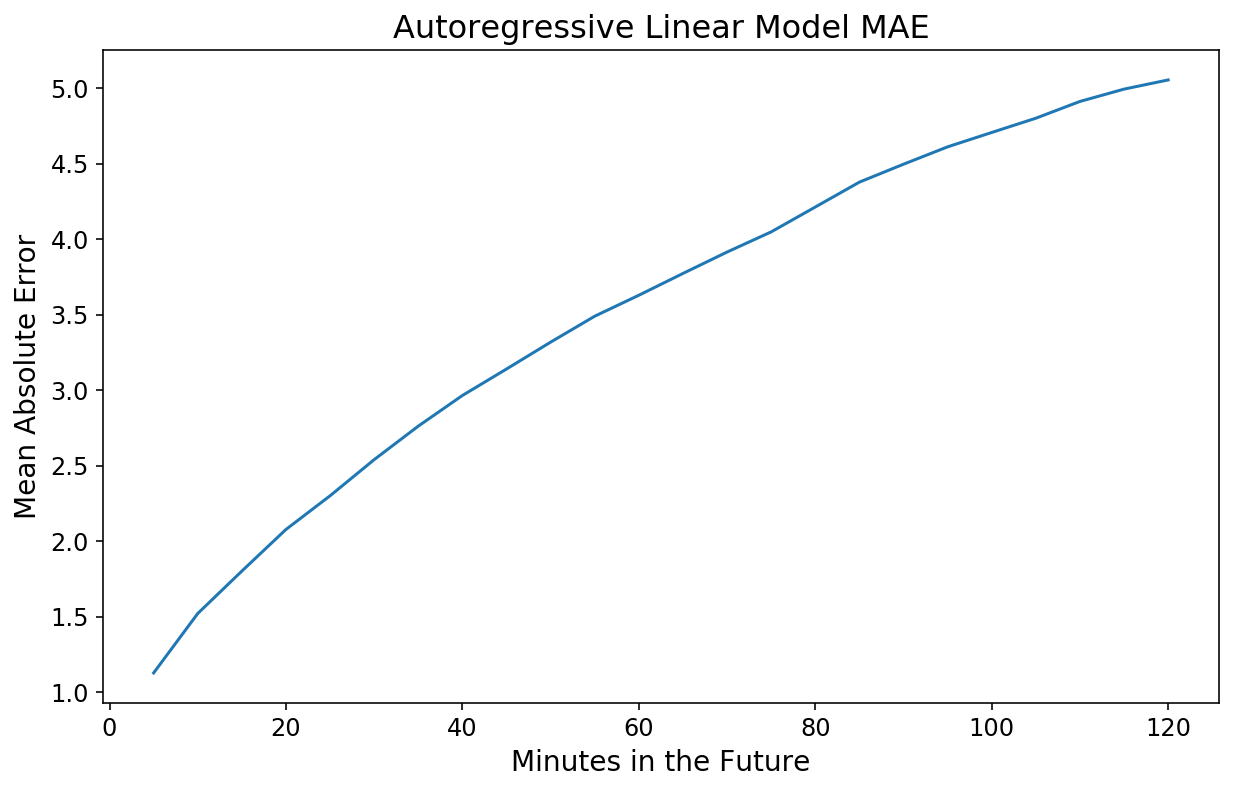
Not too shabby! Our 20-minute forecast is off by 2 bikes, on common, and our 2-hour forecast is just off by 5.
Whereas our horizon prediction seems to be fairly good, we will nonetheless check out a recursive prediction by utilizing the pipeline.forecast methodology. We’ll generate a recursive forecast, beginning at index 530 within the check information.
forecast = lin_pipeline.forecast(X,
start_idx=train_size + 530,
trans_window=samples_per_week)
plt.plot(y[-test_size+500:-test_size + 560], 'ok.-');
plt.plot(forecast[-test_size+500:-test_size + 560, 0], '-.');
plt.plot((30, 30), (0, 45));
plt.legend(['Actual Bike Availability',
'Recursive Forecast',
'Forecasting Start']);
plt.ylabel('Bike Availability');
plt.xlabel('Time Index');
plt.title('Recursive Forecast Comparability');
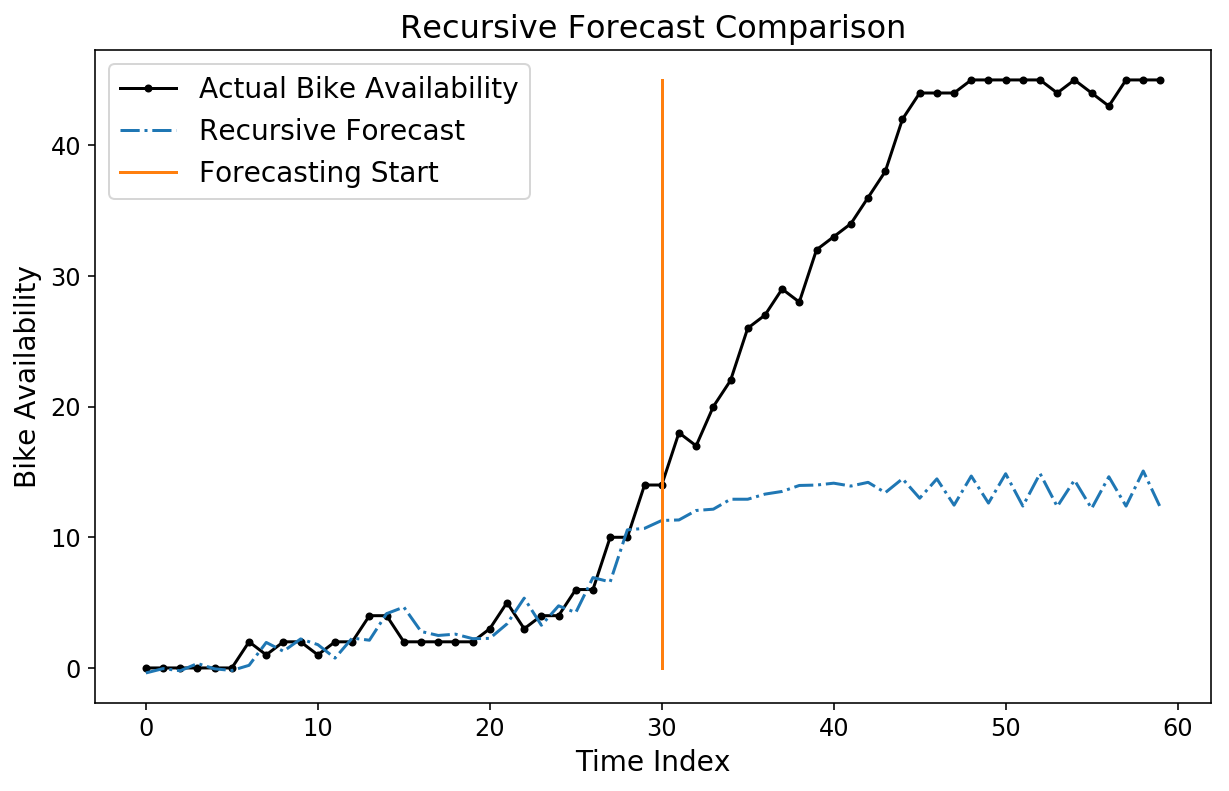
Discover how our forecast seems to be fairly unhealthy! To be truthful, it’s not essentially clear that we ought to have a superb forecast, seeing because the mannequin was skilled to optimize horizon forecasts and not recursive forecasts.
Boosters
Simply because we will, let’s attempt coaching an XGBoost mannequin for our horizon predictions, relatively than a linear regression. I don’t consider that it’s doable to instantly optimize a multioutput regression goal with XGBoost, so we are going to go the identical route as with the linear mannequin and practice 24 totally different XGBoost estimators.
from xgboost import XGBRegressor
xgb_pipeline = ForecasterPipeline([
# Convert the `y` target into a horizon
('pre_horizon', HorizonTransformer(horizon=samples_per_hour * 2)),
('pre_reversible_imputer', ReversibleImputer(y_only=True)),
('features', FeatureUnion([
# Generate a week's worth of autoregressive features
('ar_features', AutoregressiveTransformer(num_lags=samples_per_week)),
])),
('post_feature_imputer', ReversibleImputer()),
('regressor', MultiOutputRegressor(XGBRegressor(n_jobs=12,
n_estimators=300)))
])
xgb_pipeline = xgb_pipeline.match(X[:train_size], y[:train_size])
xgb_prediction = xgb_pipeline.predict(X, start_idx=train_size)
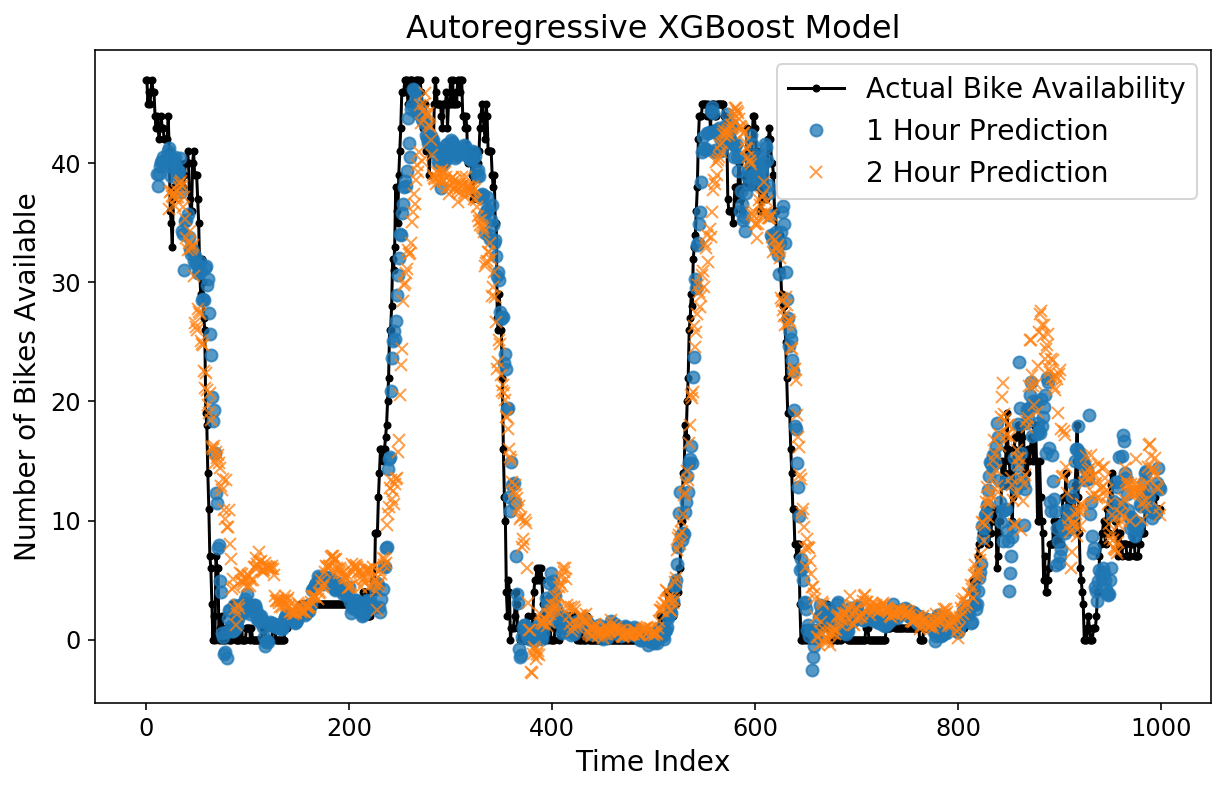
Let’s take a look at the horizon predictions. By eye, issues look higher than the linear mannequin, and the MAE plot confirms this.
plt.determine();
plt.plot(y[-test_size:], 'ok.-');
plt.plot(np.arange(11, test_size), xgb_prediction[:-11, 11], 'o', alpha=0.75);
plt.plot(np.arange(23, test_size), xgb_prediction[:-23, 23], 'x', alpha=0.75);
plt.legend(['Actual Bike Availability',
'1 Hour Prediction',
'2 Hour Prediction']);
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive XGBoost Mannequin');
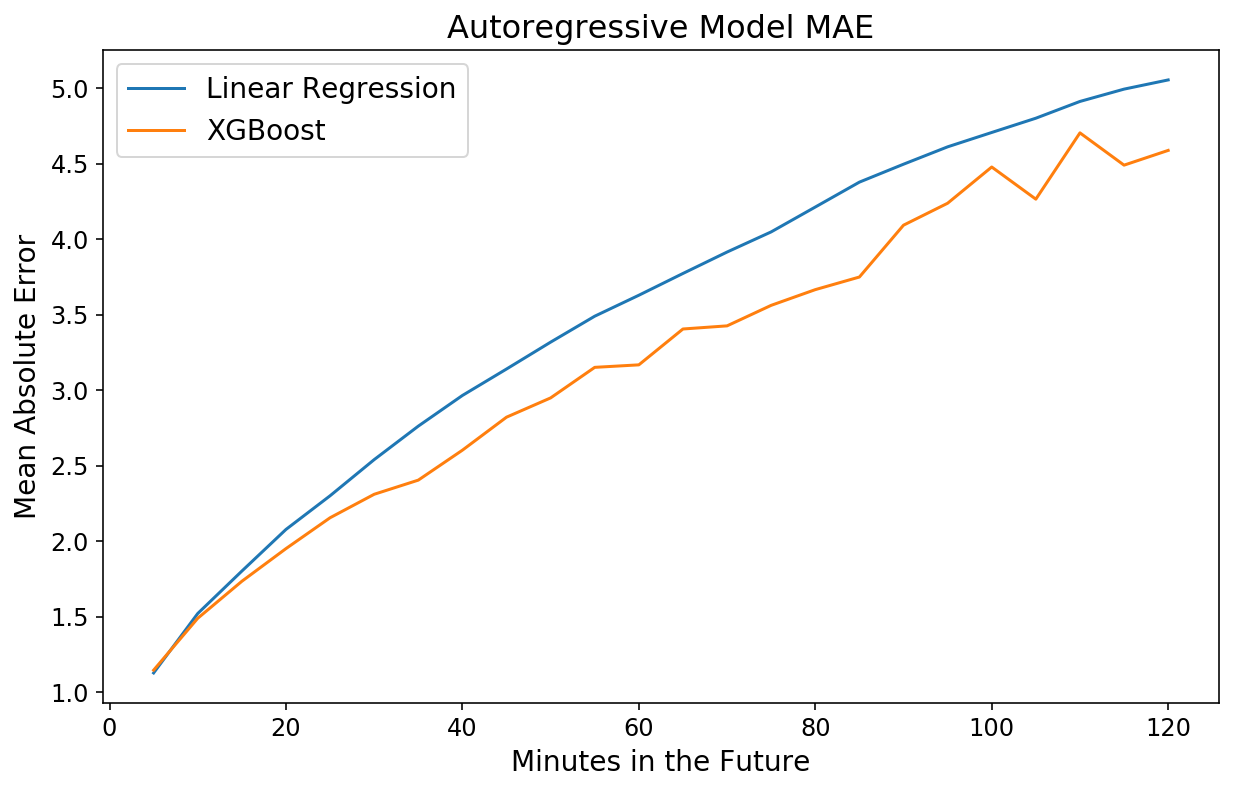
y_actual = xgb_pipeline.transform_y(X)
xgb_mae = mean_absolute_error(y_actual[-test_size:], xgb_prediction,
multioutput='raw_values')
plt.plot(np.arange(1, 25) * 5, lin_mae);
plt.plot(np.arange(1, 25) * 5, xgb_mae);
plt.xlabel('Minutes within the Future');
plt.ylabel('Imply Absolute Error');
plt.title('Autoregressive Mannequin MAE');
plt.legend(['Linear Regression', 'XGBoost']);
Deep Inside
Lastly, let’s practice a deep studying mannequin for horizon prediction. I’ve written earlier than about how a lot I like the skorch library, and we’ll use it once more right here. Through the use of skorch, we will make any PyTorch mannequin right into a scikit-learn estimator. I did some fast Googling on the most recent and best in sequence modeling with deep studying, and I got here throughout this paper that argues that utilizing convolutional neural networks for sequences is definitely higher and extra environment friendly than recurrent architectures. The authors had been sort sufficient to launch a PyTorch implementation of their code to go together with the paper, so I’m going to reuse their code beneath for creating “Temproal Convolutional Networks” (TCN).
To be clear, I perceive most likely 75% of the paper. Under is a diagram (Determine 1 from the paper) of the TCN. I might recommend studying the paper if you’re notably .
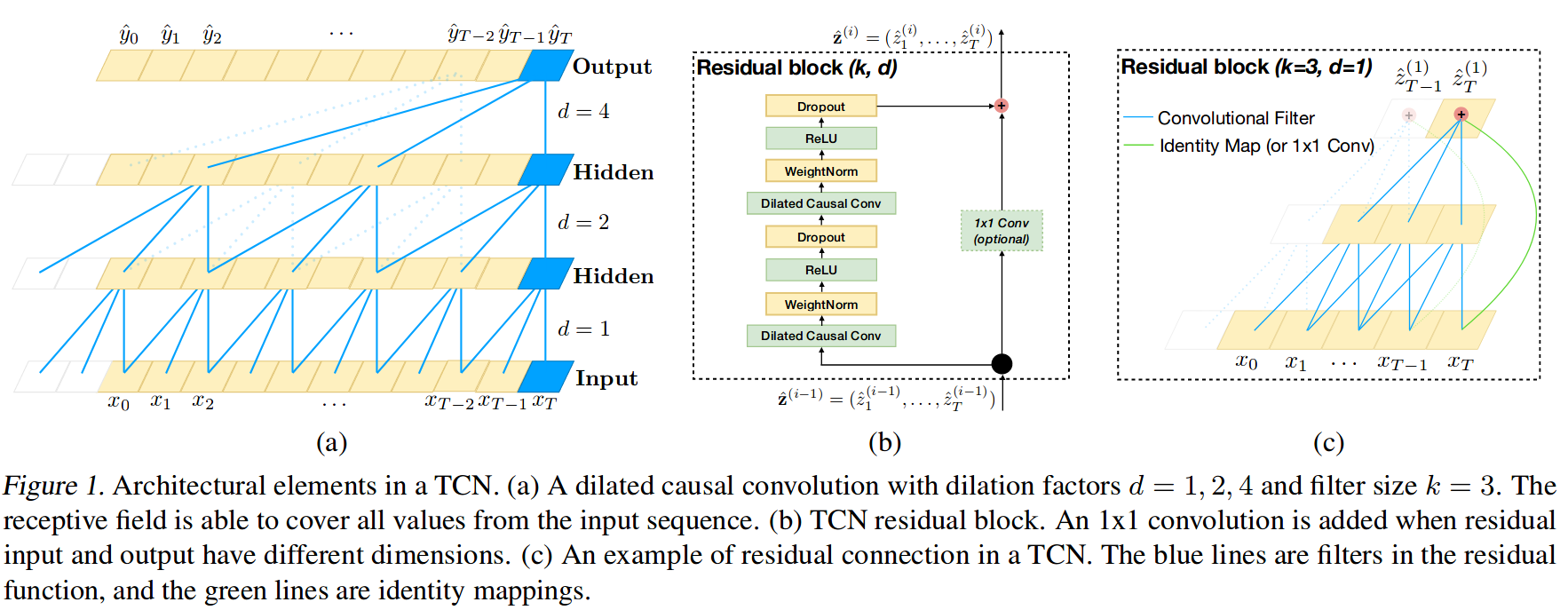
from sklearn.preprocessing import StandardScaler
from skorch.regressor import NeuralNetRegressor
from skorch.callbacks import GradientNormClipping
import torch
from torch import nn
import torch.nn.purposeful as F
from torch.nn.utils import weight_norm
"""
Under code on this cell is taken from
https://github.com/locuslab/TCN
"""
class Chomp1d(nn.Module):
def __init__(self, chomp_size):
tremendous(Chomp1d, self).__init__()
self.chomp_size = chomp_size
def ahead(self, x):
return x[:, :, :-self.chomp_size].contiguous()
class TemporalBlock(nn.Module):
def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
tremendous(TemporalBlock, self).__init__()
self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp1 = Chomp1d(padding)
self.relu1 = nn.ReLU()
self.dropout1 = nn.Dropout(dropout)
self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp2 = Chomp1d(padding)
self.relu2 = nn.ReLU()
self.dropout2 = nn.Dropout(dropout)
self.internet = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
self.conv2, self.chomp2, self.relu2, self.dropout2)
self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
self.relu = nn.ReLU()
self.init_weights()
def init_weights(self):
self.conv1.weight.information.normal_(0, 0.01)
self.conv2.weight.information.normal_(0, 0.01)
if self.downsample is not None:
self.downsample.weight.information.normal_(0, 0.01)
def ahead(self, x):
out = self.internet(x)
res = x if self.downsample is None else self.downsample(x)
return self.relu(out + res)
class TemporalConvNet(nn.Module):
def __init__(self, num_inputs, num_channels, output_sz,
kernel_size=2, dropout=0.2):
tremendous(TemporalConvNet, self).__init__()
layers = []
num_levels = len(num_channels)
for i in vary(num_levels):
dilation_size = 2 ** i
in_channels = num_inputs if i == 0 else num_channels[i-1]
out_channels = num_channels[i]
layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1,
dilation=dilation_size,
padding=(kernel_size-1) * dilation_size,
dropout=dropout)]
self.community = nn.Sequential(*layers)
self.linear = nn.Linear(num_channels[-1], output_sz)
self.last_activation = nn.ReLU()
self.output_sz = output_sz
def ahead(self, x):
batch_sz = x.form[0]
out = self.community(x.unsqueeze(1))
out = out.transpose(1, 2)
out = self.linear(out).imply(dim=1)
return out
The paper mentions utilizing default settings of 0.002 studying charge, gradient norm clipping, and ensuring that the variety of channels captures the complete historical past of the time sequence. I implement that every one beneath and practice for 60 epochs. Discover that we do not need to coach 24 totally different fashions on this case. As a substitute, our loss perform is just imply squared error throughout the complete horizon, and PyTorch is ready to mechanically calculate gradients to coach a single mannequin to optmize for the complete horizon.
internet = NeuralNetRegressor(
module=TemporalConvNet,
module__num_inputs=1,
module__num_channels=[10] * 11,
module__output_sz=2 * samples_per_hour,
module__kernel_size=5,
module__dropout=0.0,
max_epochs=60,
batch_size=256,
lr=2e-3,
optimizer=torch.optim.Adam,
machine='cuda',
iterator_train__shuffle=True,
callbacks=[GradientNormClipping(gradient_clip_value=1,
gradient_clip_norm_type=2)],
train_split=None,
)
dl_pipeline = ForecasterPipeline([
('pre_scaler', StandardScaler()),
('pre_horizon', HorizonTransformer(horizon=samples_per_hour * 2)),
('pre_reversible_imputer', ReversibleImputer(y_only=True)),
('features', FeatureUnion([
('ar_features', AutoregressiveTransformer(num_lags=samples_per_week)),
])),
('post_feature_imputer', ReversibleImputer()),
('regressor', internet)
])
dl_pipeline = dl_pipeline.match(X[:train_size].astype(np.float32),
y[:train_size].astype(np.float32),
end_idx=-5)
dl_prediction = dl_pipeline.predict(X.astype(np.float32), start_idx=train_size,
to_scale=True)
plt.determine();
plt.plot(y[-test_size:], 'ok.-');
plt.plot(np.arange(11, test_size), dl_prediction[:-11, 11], 'o', alpha=0.75);
plt.plot(np.arange(23, test_size), dl_prediction[:-23, 23], 'x', alpha=0.75);
plt.legend(['Actual Bike Availability',
'1 Hour Prediction',
'2 Hour Prediction']);
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive Deep Studying Mannequin');
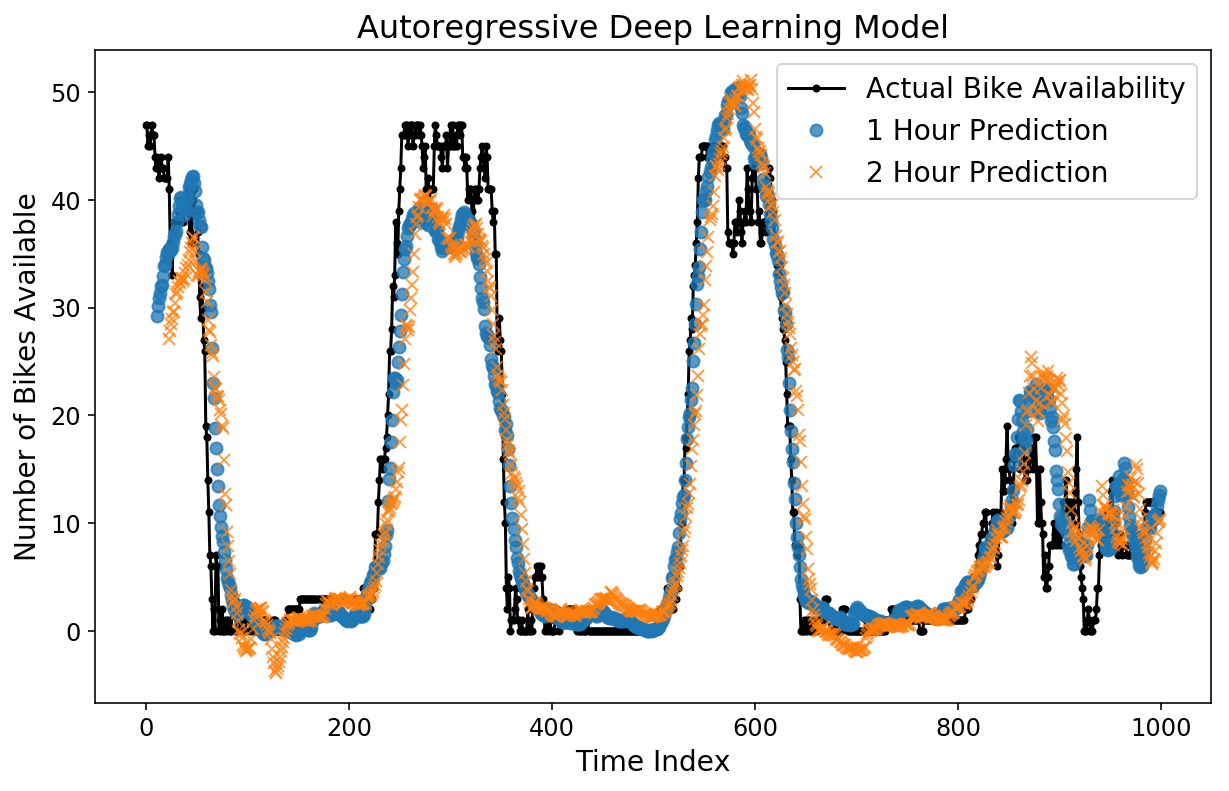
The predictions look pretty first rate by eye. Let’s take a look at the MAE.
y_actual = dl_pipeline.transform_y(X)
dl_mae = mean_absolute_error(y_actual[-test_size:],
dl_prediction,
multioutput='raw_values')
y_actual = dl_pipeline.transform_y(X)
dl_mae = mean_absolute_error(y_actual[-test_size:], dl_prediction,
multioutput='raw_values')
plt.plot(np.arange(1, 25) * 5, lin_mae);
plt.plot(np.arange(1, 25) * 5, xgb_mae);
plt.plot(np.arange(1, 25) * 5, dl_mae[:24])
plt.xlabel('Minutes within the Future');
plt.ylabel('Imply Absolute Error');
plt.title('Autoregressive Mannequin MAE');
plt.legend(['Linear Regression',
'XGBoost',
'Deep Learning']);
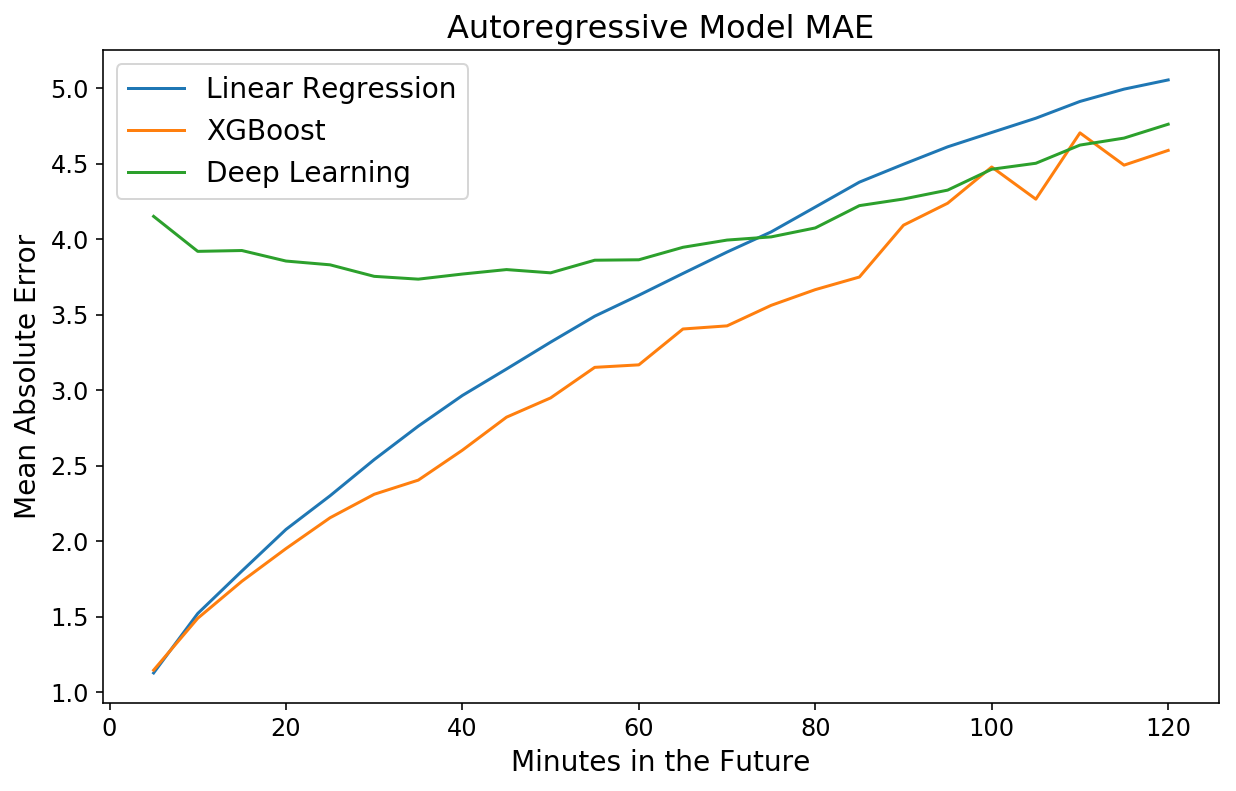
Unusually, the mannequin is worse for occasions shut sooner or later however roughly on par with XGBoost for 2-hour predictions. That is one more instance of the ability and ease of XGBoost.
I proceed to be astounded by how 1) quick and a couple of) strong to overfitting XGBoost is. My favourite machine studying library by a protracted shot.
— Sean J. Taylor (@seanjtaylor) March 1, 2017
Takeaways
On this submit, I confirmed easy methods to use the skits library to coach a supervised studying mannequin to instantly predict a time sequence horizon. We then simply ramped up the complexity of our fashions by merely slotting extra advanced fashions into our scikit-learn pipeline. At finest, we had been in a position to forecast the variety of bikes on the bike share station by my house to inside 4.5 bikes 2 hours prematurely.
I ought to notice that this submit was not a totally scientific research. To try this, I ought to have created coaching, validation, and check information units. As properly, I ought to have run a correct hyperparameter search (particularly for the deep studying mannequin!). However, I’m nonetheless assured that we will do a good job at horizon prediction.
How can we do a greater job? There are a variety of the way, which I want to discover in additional weblog posts. As a substitute of pondering of our bike availibility information as a steady time sequence to foretell, we may go together with an strategy just like ordinal regression. Moreover, we will incorporate info from different bike stations to higher predict our explicit station. Keep tuned!

