A short introduction about this ubiquitous sample and its functions
Voronoi diagrams (often known as Dirichlet tesselation or Thiessen polygons) are all over the place in nature. You’ve encountered them hundreds of instances, however perhaps didn’t name it this fashion. Voronoi diagram are easy, but they’ve unbelievable properties which have discovered functions in fields starting from cartography, biology, pc science, statistics, archaeology, all strategy to structure and humanities.
Suppose you’ve n factors scattered on a airplane, the Voronoi diagram of these factors subdivides the airplane in precisely n cells enclosing the portion of the airplane that’s the closest to the every level. This produces a tessellation that fully covers the airplane. As an illustration, in Determine 1, I plotted 100 random factors and their corresponding Voronoi diagram. As you possibly can see, each level is enclosed in a cell, whose boundaries are precisely equidistant between two or extra factors. In different phrases, all the world enclosed within the cell is closest to the purpose within the cell than to another level.
Supply: Picture by creator
Voronoi patterns in nature
The sample created by Voronoi diagrams is a standard one in nature. In Determine 2, I made a small collage of some naturally occurring Voronoi-like patterns. From microscopic cells in onion skins, to the shell of jackfruits and the coat of giraffes. These patterns are all over the place!
A primary motive for his or her omnipresence is that they type environment friendly shapes. As we talked about earlier, Voronoi diagram fully tessellates the plan: therefore, all area is used. That is very handy in case you are making an attempt to squeeze as a lot as potential in a restricted area — corresponding to in muscle fibres or bee hives. Secondly, Voronoi diagrams are a spontaneous sample every time one thing is rising at a uniform development fee from separate factors (see Determine 3). As an illustration, this explains giraffe exhibit such patterns. Giraffe embryos have a scattered distribution of melanin-secreting cells, which is accountable for the darkish pigmentation of the giraffe’s spots. Over the course of the gestation these cells launch melanin — therefore spots radiate outward. reader could discuss with this paper, wherein the authors use Voronoi diagrams to mannequin pc rendering of spots on animals coats.

(From top-left to backside proper: cross-section of a muscle, giraffes coat patterns, wings of a dragonfly, garlic bulb, corns, jackfruits hanging from a tree.)
Supply: Wikipedia, Nirav Shah, Karolina Grabowska, StarGlade, , Mali Maeder, Abi Jacob

Supply: Wikipedia
Voronoi sample in structure and humanities
Maybe due to their spontaneous “pure” look, or just due to their mesmerising randomness, Voronoi patterns have deliberately been applied in human-made constructions. An architectural instance is the “Water dice” constructed to deal with the water sports activities through the 2008 Beijing Olympics. It options Voronoi diagrams on its ceiling and façades (Determine 4). The Voronoi diagrams have been chosen as a result of they recall bubbles 1 . This analogy may be very clear at night time, when your complete façade is illuminated in blue and comes alive.

Supply: Wikipedia,
However Chinese language appreciation of Voronoi sample is unquestionably older than this constructing. Guan and Ge ware from the Track dynasty have a particular crackled glaze. Ceramics can simply crack through the cooling course of, nevertheless the crackles from the Guan and Ge ware are totally different — they’re intentional. They’re wanted due to their aesthetic qualities. Because of the Voronoi-like patterns on their floor, each bit is exclusive. To this point, this is likely one of the most imitated kinds of porcelain (Determine 5).

Supply: Wikipedia, Wikipedia
Voronoi diagrams are additionally frequent in graphic arts for creating “summary” patterns. I believe they make glorious background photographs. For instance, I created the thumbnail of this submit by producing random factors and establishing a Voronoi diagram. Then, I colored every cell based mostly on the gap of its level from a randomly chosen spot within the field (Determine 6). Countless “summary” backgrounds photographs could possibly be generated this fashion.

Supply: Picture by creator
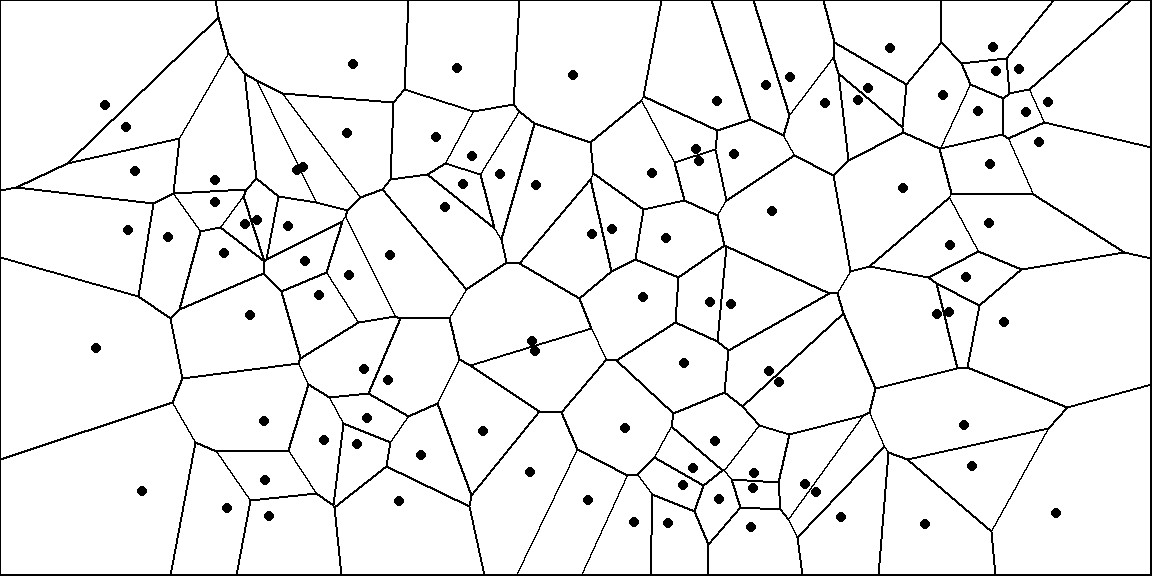
To this point, we’ve introduced a easy two-dimensional Voronoi diagram. Nevertheless, the identical kind of construction could be generalised to an n-dimensional area. Suppose P={p1,p2,…,pm} is a set of m factors in our n-dimensional area. Then, the area could be partitioned in m Voronoi cells, Vi, containing all factors in Rn which can be nearer to pi than to another level.
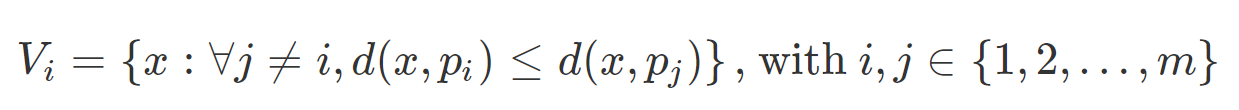
The place the operate d(x,y) provides the gap (a) between its two arguments. Sometimes, the Euclidean distance is used (l2 distance):
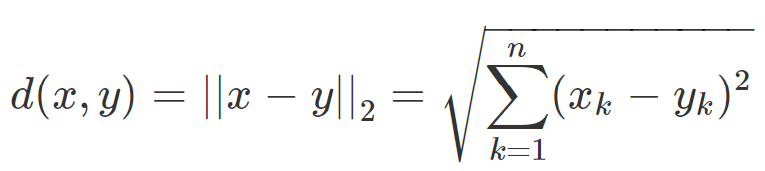
Nevertheless, Voronoi diagrams could possibly be designed utilizing different distance capabilities. As an illustration, Determine 7 exhibits a Voronoi diagram obtained with the Manhattan or cityblock distance (l1l1 distance). The Manahattan distance is the gap between two factors if you happen to needed to observe a daily grid — corresponding to town blocks of Manhattan. The result’s a extra “boxy” Voronoi diagram.

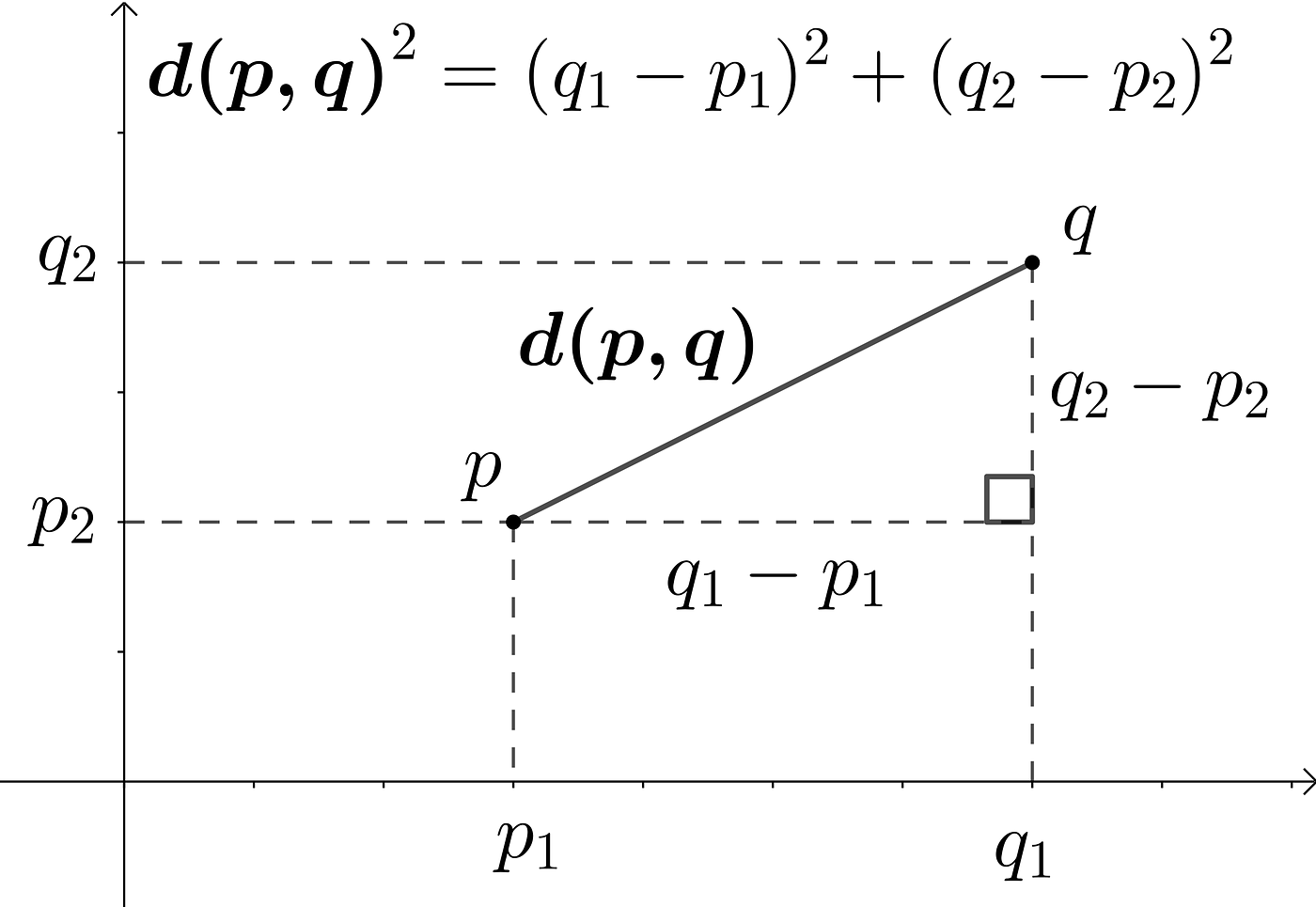
Supply: Wikipedia

Supply: Wikipedia
Euclidean distance is the commonest distance measure in scientific functions of the Voronoi diagram. It additionally has the benefit of producing Voronoi cells which can be convex. That’s to say, if you happen to take any two factors inside a cell, the road that connects the 2 factors will lie totally inside the cell.
Lastly, it must also be famous that Voronoi diagrams are tightly linked with the k-nearest neighbours algorithm (k-NN) — a highly regarded algorithm in classification, regression and clustering issues. The algorithm makes use of the kk closest examples within the coaching dataset to make worth predictions. Because the Voronoi diagrams partitions the area in polygons containing the closest factors to every seed, the perimeters of Voronoi cells correspond precisely to the choice boundaries of a easy 1-nearest neighbour drawback.
In case you take every of the factors from a Voronoi diagram and hyperlink it with the factors in its neighbouring cells, you’ll get hold of a graph known as Delaunay triangulation. In mathematical phrases, the Delaunay triangulation is the twin graph of the Voronoi diagram. Within the Determine under, a Voronoi diagram (black) and Delaunay triangulation (gray) is plotted from a set of factors.
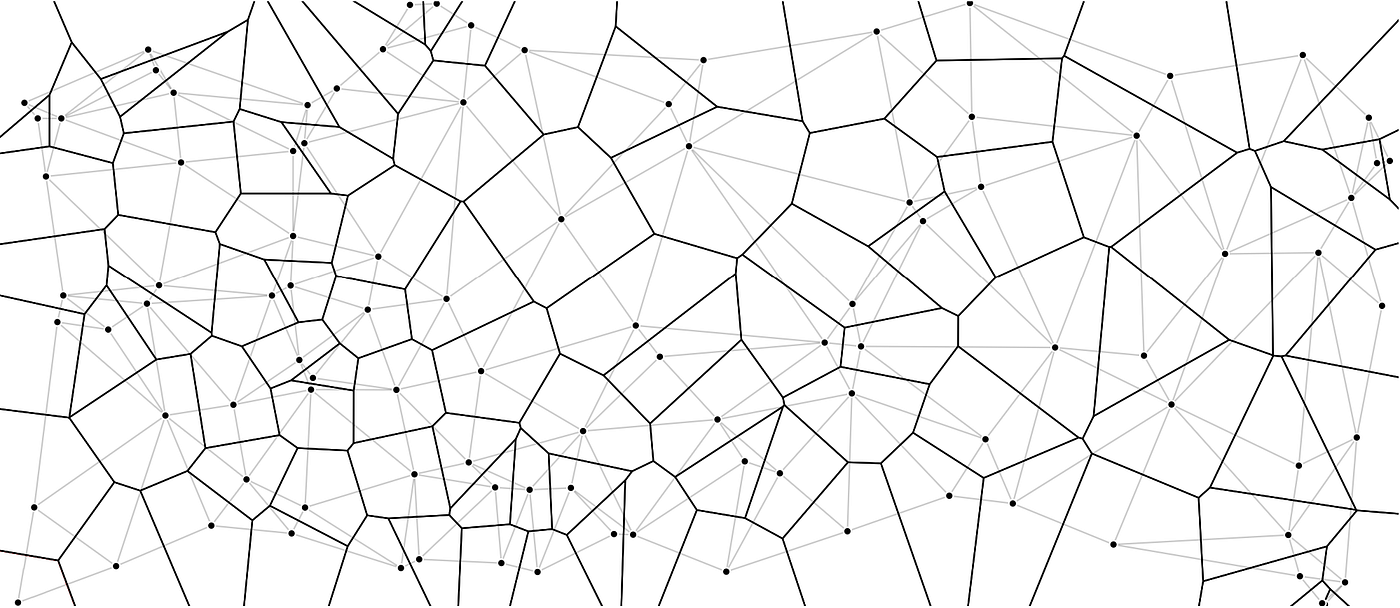
Supply: Picture by creator
Delaunay triangulation is simply as wonderful as Voronoi diagrams. Because the identify suggests, it produces a set of triangles linking our factors. These triangles are such that if one have been to attract a circle throughout the vertices of those triangles, there could be no different level contained in the circle (See Determine 10). Furthermore, Delaunay triangulation additionally has the property of maximising the smallest angle of within the triangles of the triangulation. Therefore, Delaunay triangulation tends to keep away from triangles with acute angles.

Supply: Wikipedia
These properties make it very helpful in modelling surfaces and objects from a set of factors. As an illustration, the Delaunay triangulation is used to generate meshes for the finite component technique, assemble 3D fashions for pc animations and mannequin terrain in GIS evaluation.
Llyod’s algorithm is a helpful algorithm associated to Voronoi diagrams. The algorithm consists in repeatedly alternating between establishing Voronoi diagrams and discovering the centroids (i.e. middle of mass) of every cell (See Determine 12). At every iteration, the algorithm areas the factors aside and produces extra homogeneous Voronoi cells.
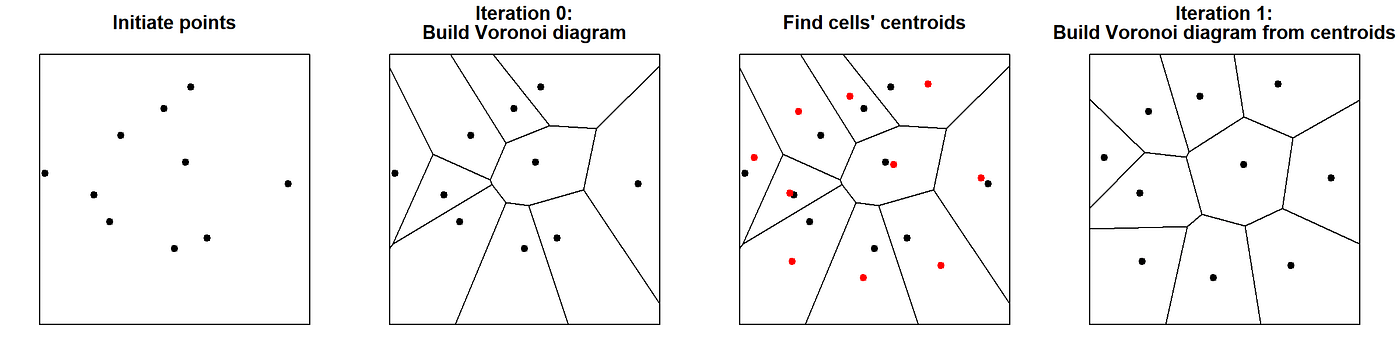
Supply: Picture by creator
After a number of iterations, the cells will have already got a “rounder” facet and factors might be extra evenly distributed. That is illustrated within the determine under, wherein I’ve plotted the primary 30 iterations of the Lloyd’s algorithm for a random set of factors. For every level, I additionally file their beginning place (gray hole circle) to higher hint the motion of every cell. For top variety of iterations, the diagram tends to converge in the direction of a secure Voronoi diagram wherein each seed can be the centroid of the cell — often known as the centroidal Voronoi diagram. Apparently, in 2D, Voronoi cells will have a tendency to show into hexagons as a result of they supply essentially the most environment friendly approach of of packing shapes in a airplane. As any bee constructing their hive can certify, hexagonal cells have two massive benefits: 1) they guarantee no empty area is left between cells (i.e. tessellates the airplane), and a couple of) hexagons supply the best ratio between floor and perimeter of the cell. This so-called Honeycomb conjecture, took mathematicians two-thousand years to show.
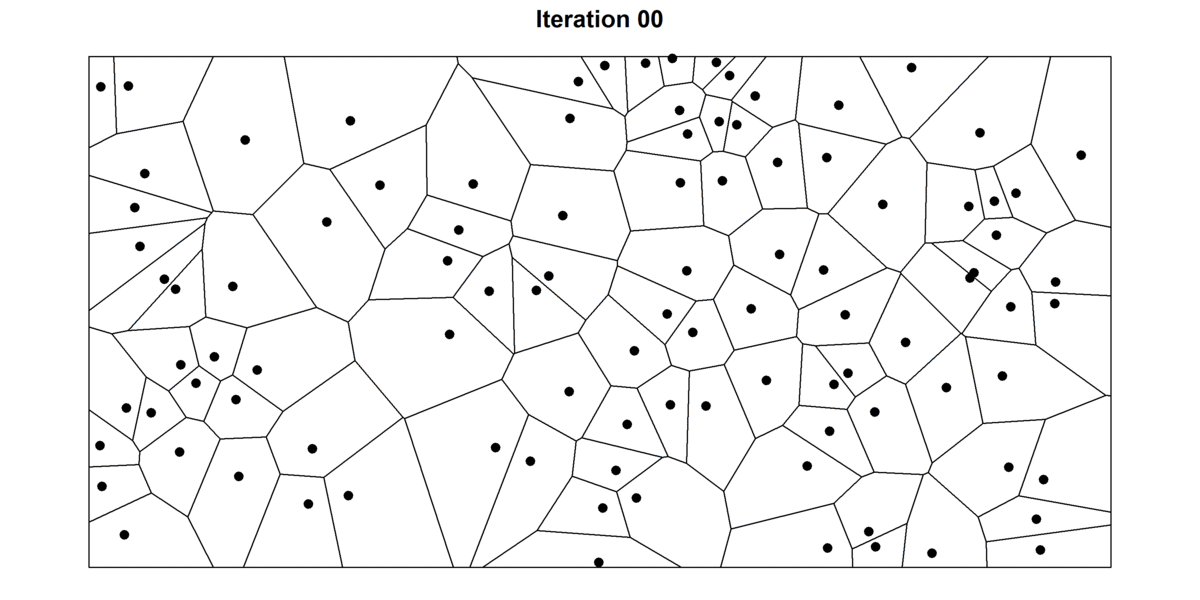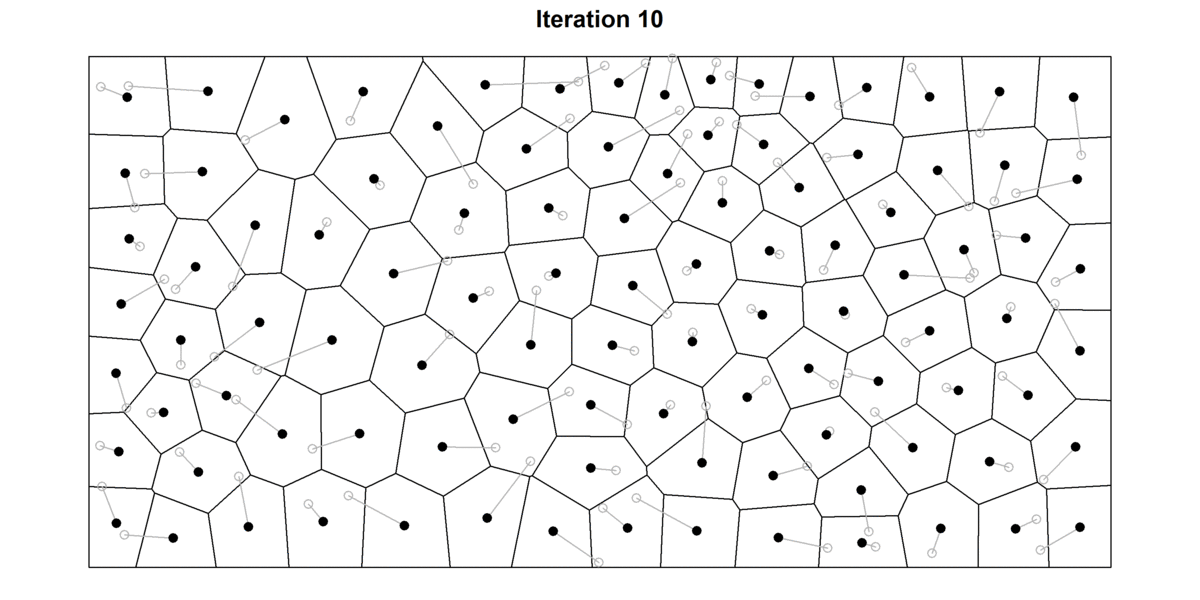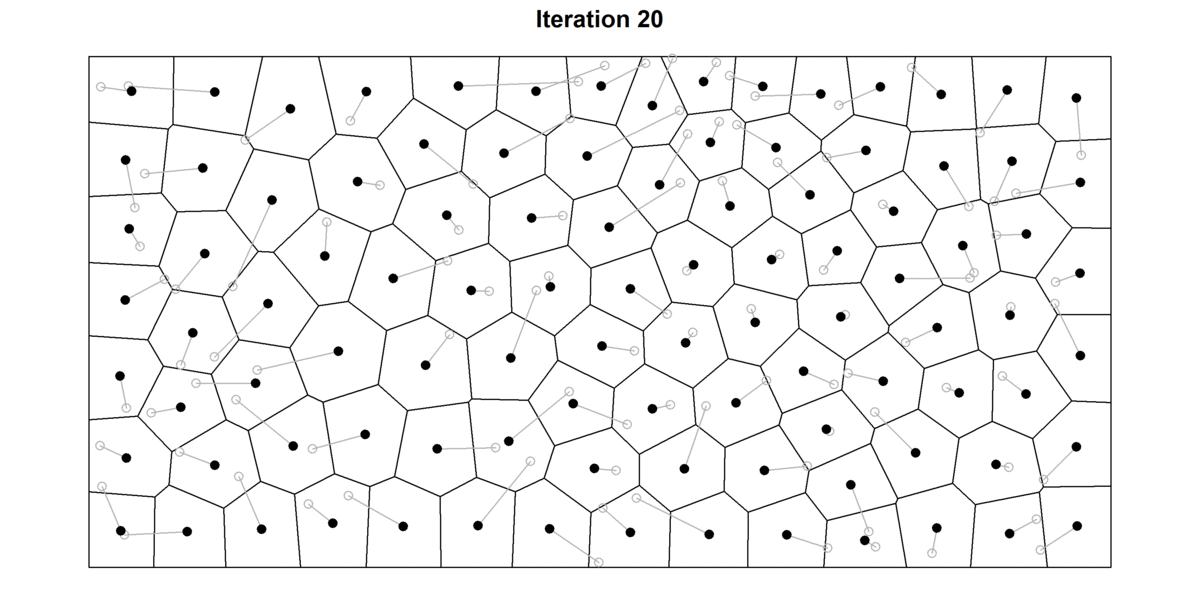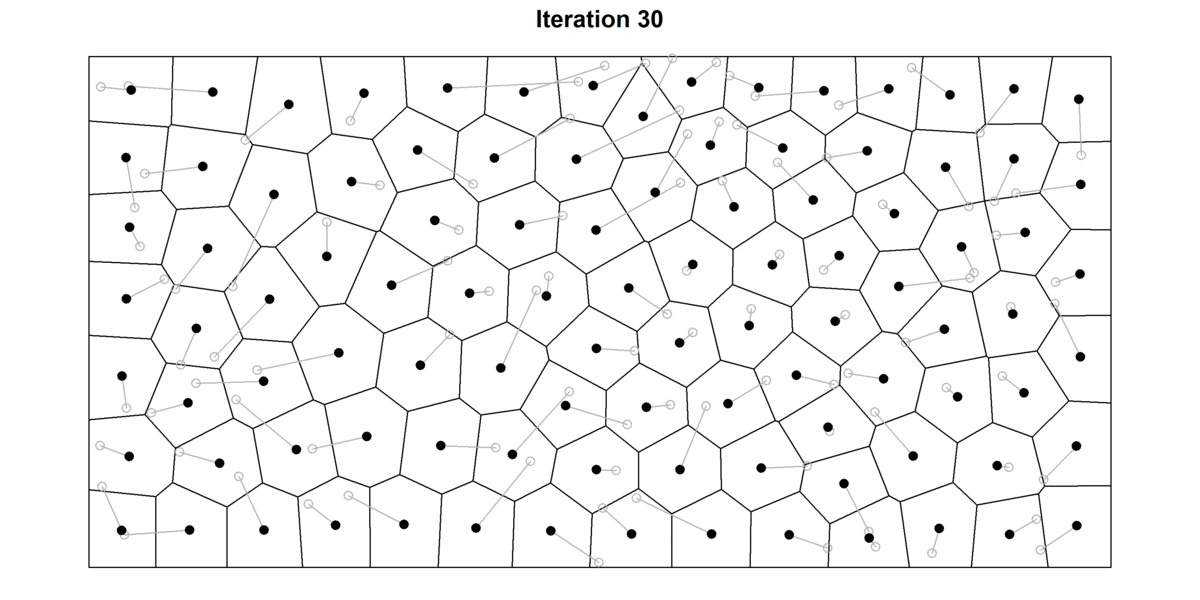
Supply: Picture by creator
In knowledge science, Lloyd’s algorithm is on the foundation of k-means clustering — one of the in style clustering algorithms. k-means clustering is often initiated by taking kk random “centroids” in area. Then, knowledge factors are grouped in kk clusters by alternating between 1) assigning knowledge factors to the closest “centroid” (that is equal to constructing a Voronoi diagram for the centroid and checking which level are contained in the cell) and a couple of) updating the centroid by calculating the imply of the factors inside every cell (See Determine 14).
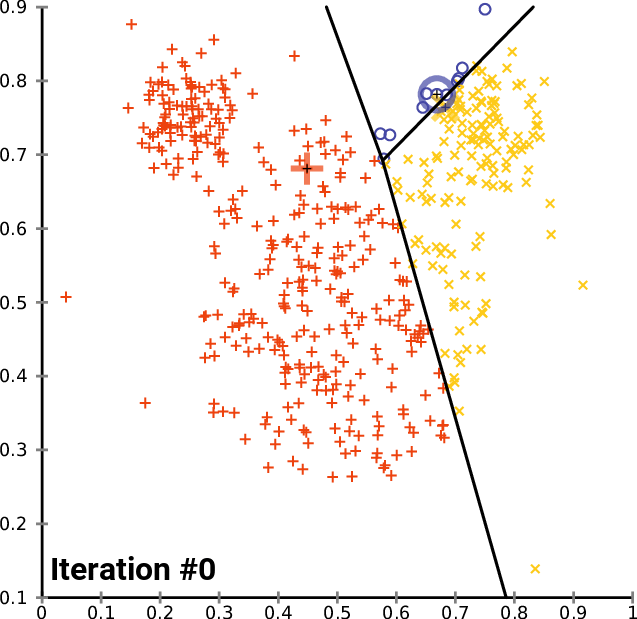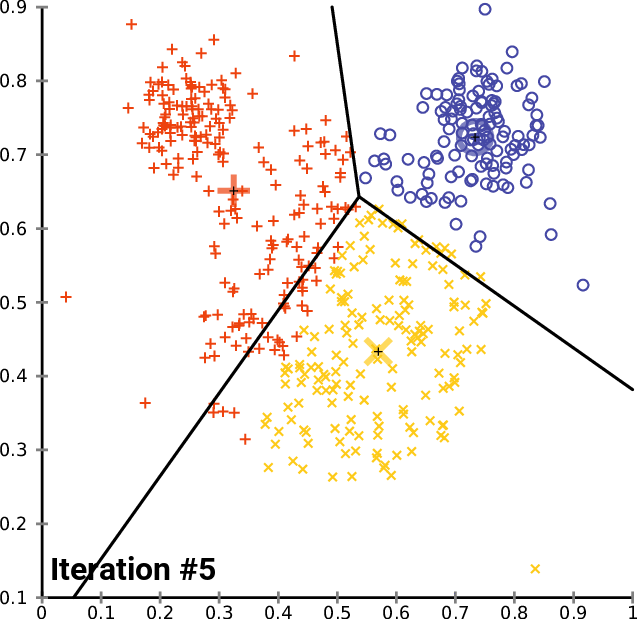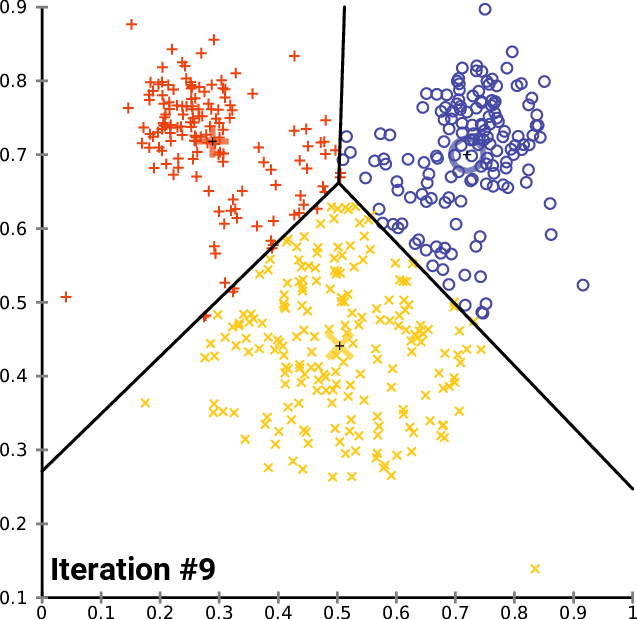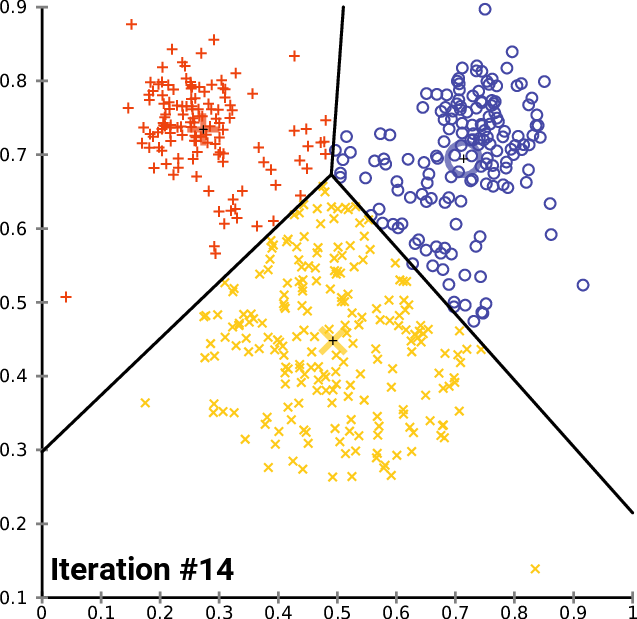
Soruce: Wikipedia
In addition to knowledge science, Lloyd’s algorithm is utilized in quite a lot of functions. As an illustration, it is vitally frequent in quantization and lossy knowledge compression algorithms (e.g. Lloyd-Max algorithm). It is usually very helpful every time one desires random factors which can be properly spaced. As an illustration, it could possibly be used to easy meshes generated from the Delaunay triangulation, for dithering photographs, or as a foundation for procedural maps era in video video games.
One may assemble Voronoi diagrams by constructing every cell one after the other. If one extends the bisector of the segments linking each mixture of factors, it’s potential to acquire the define of Voronoi cells (Determine 15). Nevertheless, this system is kind of inefficient. Contemplating there are 0.5*(1−n)n mixtures of factors, the complexity of such algorithm would enhance quadratically with the variety of factors.

Supply: Picture by creator
Extra environment friendly options have been proposed. For instance, the Sweep line algorithm builds Voronoi cells progressively by sequentially utilizing binary search tree and precedence queue operations (Determine 16). A great description of this algorithm could be discovered right here. One other approach of establishing Voronoi diagrams, is to first construct Delaunay triangulations. As soon as the triangulation is obtained, extending the bisectors of the triangle edges results in the Voronoi diagram. Delaunay triangulation could be obtained with out the necessity of contemplating each pair of factors. As an illustration, an environment friendly method consists in projecting the factors on a paraboloid in a better dimension. Re-projecting again the convex hull onto the unique area provides the Delaunay triangulation.

Supply: Wikipedia
A dialogue of various algorithms for computing Voronoi diagram and their complexity is obtainable right here, right here, and right here. New algorithms are repeatedly being proposed to enhance computation effectivity in numerous circumstances (e.g. Yan et al. 2011, Qin et al. 2017). There are additionally strategies requiring fixed time that generate approximate Voronoi diagrams (e.g. Leap flooding algorithm).
- This text tells the story of how Voronoi diagrams have been utilized by John Snow to point out the hyperlink between water pumps and the transmission of Cholera through the 1854 London outbreak.
- Amil Patel has an outstanding weblog on recreation growth. I extremely advocate his posts on procedural map era with Voronoi diagrams.
- This submit by David Austin provides an incredible clarification of the Sweep line algorithm for computing Voronoi diagrams.
- This good wanting map by Jason Davies is a Voronoi diagram of the situation of airports all over the world.
- Spatial Tessellations: Ideas and Purposes of Voronoi Diagrams is a bible on Voronoi diagrams. When you have any doubt about Voronoi diagrams, you’ll actually discover a solution right here.
- These slides from Vincent Legat have some lovely drawings for various building algorithms.
- Voronoi diagrams are generally used to mannequin timber in forests (e.g. Abellanas et al. 2016, Bohler et al. 2018).
- Voronoi diagrams can be used to find out robotic’s paths. Test these articles: article 1, article 2.
- Voronoi diagrams have thousand of functions. From modelling timber in a forest to planning robotic paths. On this article I barely scratched the floor. These hyperlinks include lists of attention-grabbing functions: hyperlink 1, hyperlink 2, link3, link4, hyperlink 5.
This text was initially printed right here:


