The best way to choose the most effective set of options utilizing SVM?

Help Vector Machine (SVM) is without doubt one of the supervised machine studying algorithms that can be utilized for both regression or classification modeling. It is without doubt one of the machine studying algorithms that’s most popular over varied algorithms because it helps yield increased and higher accuracies. SVM operates on the precept of the Kernel trick and it’s best appropriate for binary classification duties because the SVM may have minimal lessons to function on close to the hyperplane and it additionally converges sooner. So on this article allow us to see easy methods to extract the most effective set of options from the info utilizing SVM utilizing varied function choice methods.

Desk of Contents

1. Introduction to SVM
2. Ahead Function Choice utilizing SVM
3. Backward Function Choice utilizing SVM
4. Recursive Function choice utilizing SVM
5. Mannequin constructing for the options chosen by the recursive approach
6. Abstract

Introduction to SVM

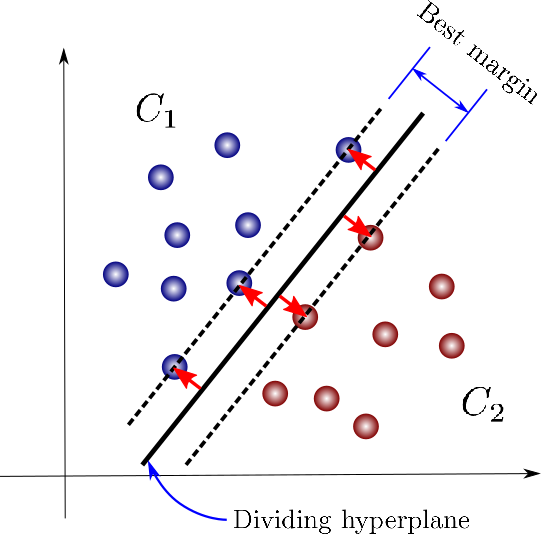
Help Vector Machine (SVM) is without doubt one of the supervised machine studying algorithms which can be utilized for both classification or regression. Among the many varied supervised studying algorithms, SVM is one such algorithm that may be very sturdy and helps in yielding increased mannequin accuracies when in comparison with different algorithms. 

The SVM operates on the underlying precept of the Kernel trick the place the algorithm will probably be liable for discovering the optimum hyperplane for operating on the whole options current within the dataset and the options near the hyperplane will probably be categorized into the respective lessons. SVM algorithm is finest fitted to classification issues. 

Are you in search of a whole repository of Python libraries utilized in knowledge science, try right here.

Now allow us to see easy methods to implement an SVM classifier and choose the most effective options of the dataset utilizing SVM among the many varied options that will probably be current within the dataset.

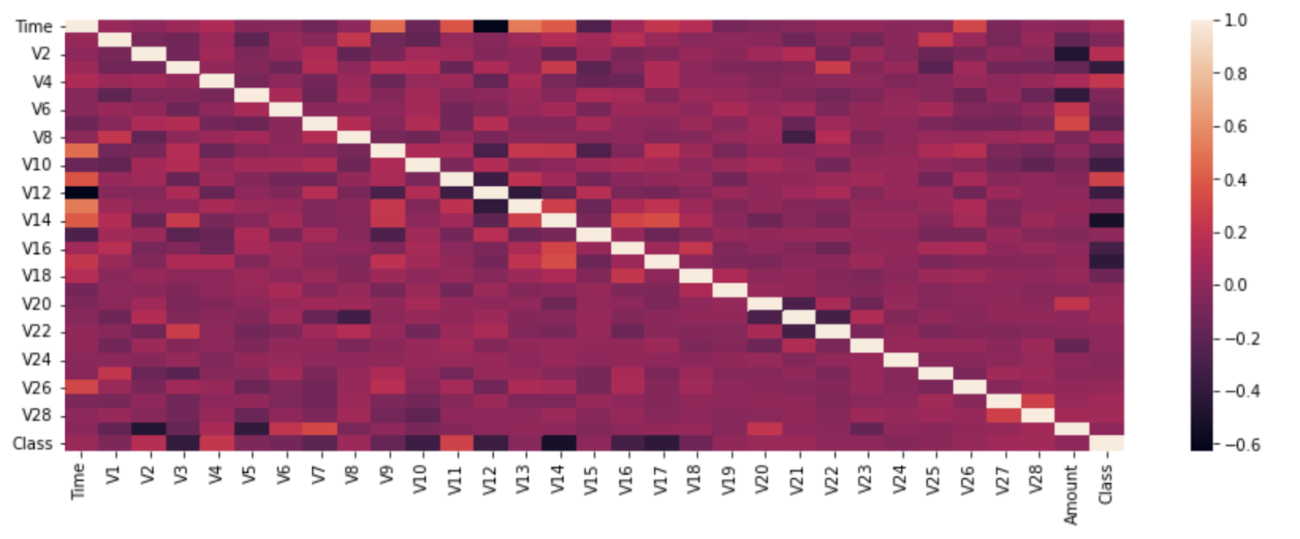
Earlier than continuing forward with the function choice methods allow us to see the correlation current within the dataset we’re working with via a heatmap.

plt.determine(figsize=(15,5))
sns.heatmap(df.corr())
plt.present()

Processing the info earlier than implementing SVM

For SVM mannequin constructing the info ought to be standardized on a standard scale. So right here at first, the info was break up into practice and check and the info was standardized utilizing the StandardScaler module of the Scikit Study Preprocessing package deal.

from sklearn.model_selection import train_test_split
X=df.drop('Class',axis=1)
y=df['Class']
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.2,random_state=42)
from sklearn.preprocessing import StandardScaler
ss=StandardScaler()
X_trains=ss.fit_transform(X_train)
X_tests=ss.fit_transform(X_test)

So now as we have now standardized the dependent options of the dataset let’s proceed forward with mannequin constructing.

Constructing an SVM Mannequin

Right here the principle moto is to pick necessary options from the dataset utilizing SVM so allow us to see easy methods to import the required libraries for SVM classification and match the SVM classifier mannequin on the break up knowledge.

from sklearn.svm import SVC
svc=SVC()
svc.match(X_trains,Y_train)

Ahead Function Choice utilizing SVM

The Ahead function choice approach works in a manner whereby at first a single function is chosen from the dataset and later all of the options are added to the function choice occasion and later this occasion object can be utilized to judge the mannequin parameters. The mlxtend module was used for the function choice whereby an occasion was created for Ahead function choice and later that occasion object was used to suit on the break up knowledge and later the R-squared worth was used to judge the options chosen by the ahead function choice approach.

!pip set up mlxtend
import joblib
import sys
sys.modules['sklearn.externals.joblib'] = joblib
from mlxtend.feature_selection import SequentialFeatureSelector as sfs

forward_fs_best=sfs(estimator = svc, k_features="finest", ahead = True,verbose = 1, scoring = 'r2')
sfs_forward_best=forward_fs_best.match(X_trains,Y_train)

So right here we will see that the function choice approach has iterated via all of the 30 options current within the dataset and later that occasion can be utilized to judge the variation defined by the options being chosen.

print('R-Squared worth:', sfs_forward.k_score_)

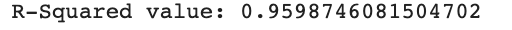
Right here we will see that the ahead function choice approach is liable for explaining 96% of the variation within the knowledge. In the identical manner, allow us to see easy methods to implement the backward function choice approach.

Backward Function Choice utilizing SVM

The backward function choice approach on the first considers all of the options of the dataset and later at every occasion one function of the dataset is dropped and the options current in that occasion are evaluated for optimum function choice. Now allow us to see easy methods to implement the backward function choice approach.

backward_fs_best=sfs(estimator = svc, k_features="finest", ahead = False,verbose =1, scoring = 'r2')
sfs_backward_best=backward_fs_best.match(X_trains,Y_train)

print('R-Squared worth:', sfs_backward_best.k_score_)

So right here we will see that the backward function choice approach is explaining 88.62% of the variation within the knowledge. This is likely to be because of the increased options chosen within the first occasion. So for a better option allow us to see the power of the Recursive Function Choice approach.

Recursive Function choice utilizing SVM

The recursive function choice approach is a reproduction of the backward choice approach however it makes use of the precept of function rating for choosing the optimum options and attributable to this it’s noticed that this function choice approach performs higher than the ahead function choice approach. Allow us to see easy methods to implement this function choice approach.

X_trains_df=pd.DataFrame(X_trains,columns=X_train.columns)
from sklearn.feature_selection import RFE
svc_lin=SVC(kernel="linear")
svm_rfe_model=RFE(estimator=svc_lin)
svm_rfe_model_fit=svm_rfe_model.match(X_trains_df,Y_train)
feat_index = pd.Collection(knowledge = svm_rfe_model_fit.ranking_, index = X_train.columns)
signi_feat_rfe = feat_index[feat_index==1].index
print('Vital options from RFE',signi_feat_rfe)

Now allow us to examine the unique variety of options that have been current within the dataset and the variety of options which might be chosen as optimum options by the recursive function choice approach.

print('Unique variety of options current within the dataset : {}'.format(df.form[1]))
print()
print('Variety of options chosen by the Recursive function choice approach is : {}'.format(len(signi_feat_rfe)))

So right here we will clearly see that nearly solely 50% of the options current within the dataset are helpful when in comparison with the whole dataset. So now allow us to construct a mannequin utilizing these chosen options by the Recursive function choice approach.

Mannequin constructing for the options chosen by the recursive approach

Utilizing the options chosen by the recursive function approach allow us to create a subset of the coaching knowledge and create a brand new mannequin occasion of SVM and match it on the subset of the options chosen and allow us to observe the R-squared worth for the optimum set of options being chosen by the recursive approach.

X_trains_new=X_train[['V1', 'V2', 'V4', 'V6', 'V9', 'V10', 'V12', 'V14', 'V17', 'V18', 'V19',
      'V20', 'V25', 'V26', 'V28']]
rfe_svm=SVC(kernel="linear")
rfe_fit=rfe_svm.match(X_trains_new, Y_train)
print('R2 squared worth for RFE',rfe_fit.k_score_)

Abstract

So that is how the most effective set of options are chosen utilizing SVM by using varied function choice methods and decreasing the issues related to working underneath increased dimensionality of information. This method reduces the scale of the dataset the place the optimum set of options can be utilized as a subset for respective mannequin constructing and yield dependable mannequin parameters and efficiency because the mannequin operates with an optimum set of options chosen by the function choice methods.

References