Bodily understanding of the pattern imply
Probably all of us (not solely information science individuals) used to compute the pattern imply. Everybody is aware of the straightforward formulation for the pattern imply. It’s merely the sum of the observations divided by their quantity, i.e. the arithmetic imply. Nonetheless, what’s the understanding of it, what does its worth computed for sure information imply, and what do its traits bodily imply and translate. And what does it really imply to be the pattern imply? I’ll reply such profound questions on this story by explaining the essence of the pattern imply, its bodily definition, and interpretation. Due to this understanding, it is going to be simpler and extra intuitive to have some properties of the pattern imply with out pointless calculations.
Let us begin with the straightforward formulation for the pattern imply. It’s simply the arithmetic imply, i.e. the sum of all observations divided by the size of our pattern. For the pattern (X1, X2, …, Xn) we have now:
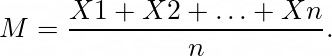
However have you ever ever puzzled why simply such an arithmetic imply talks about one thing common, about some common habits, a median property of information? Why there’s a sum of observations on this formulation, a sum of numbers, and never another mathematical operation, e.g. multiplication. Going additional, why will we divide such plenty of observations by their quantity, why will we divide? A key downside in educating concerning the imply, and understanding it, is that the formulation for the pattern imply isn’t its definition, however a consequence of the definition. So what’s the definition of the pattern imply?
Definition: The pattern imply M for a pattern of information is a quantity for which the sum of distances to smaller observations than M from the pattern (factors from the left aspect of M) is the same as the sum of distances to better observations than M from the pattern (factors from the precise aspect of M).
This definition may very well be rewritten mathematically as the next equation. Allow us to assume that we possess a pattern of information (X1, X2, …, Xn), then the equation characterizing the pattern imply is

the place

The indicator from the left-hand aspect of the equation checks if the statement Xi is beneath (or equal to) the pattern imply M, and the indicator from the right-hand aspect of the equation checks if the statement Xi is above the pattern imply M. If we remedy the equation above with respect to the unknown variable M, we acquire precisely the usual well-known formulation for the arithmetic imply. So, the formulation for the pattern imply is only a consequence of the definition.
Maybe this definition and equation are obscure at first look, however let’s attempt to digest them on a easy instance. Allow us to assume that we have now such a knowledge pattern (X1, X2, X3, X4, X5, X6, X7)=(1, 2.3, 4.5, 7, 8.1, 9.8, 3.1). The pattern imply for our pattern is M=5.28. Knowledge beneath the pattern imply are (X1, X2, X7)=(1, 2.3, 3.1) and above the pattern imply (X3, X4, X5, X6)=(5.5, 7, 8.1, 9.8). Allow us to see our information on the quantity axis beneath.

And now, allow us to verify the distances from the pattern imply to the observations in our pattern.

In accordance with the definition above and the equal equation sum of distances to the factors beneath the pattern imply ought to equal the sum of distances to the factors above the pattern imply. Allow us to take a look beneath.

In our pattern, the sum of distances to the factors beneath the pattern imply equal 9.37 and is identical for the sum of distances to the factors above the pattern imply. Therefore, the pattern imply give us the ‘heart of the stability’ for distances between factors from our pattern to itself, please see the determine beneath.

Now, if we already really feel and perceive what the pattern imply M means for our information, let me level out some properties which needs to be now extra intuitive and clear.
- The distinctiveness of the pattern imply.
Allow us to assume for a second what if the candidate for the common of our information had been a special quantity. What is going to occur if we barely shift the pattern imply, please see the determine beneath.
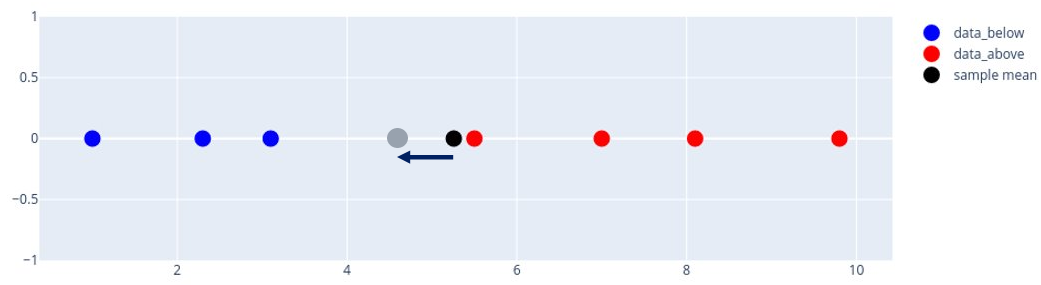
Allow us to verify now the distances to the factors from our pattern from a brand new candidate, please see the determine beneath.

What needs to be intuitively clear with this new candidate for the pattern imply (shifted pattern imply) we lose the stability of our distances, please see the determine beneath.

Due to this fact, we will say that the quantity M satisfying the definition of the pattern imply is uniquely decided. There is no such thing as a different level on the quantity axis satisfying the definition of the pattern imply and equivalently holding the stability for distances to the factors of our pattern from itself.
2. A degree not affecting the pattern imply.
Allow us to introduce a notation for a pattern (X1, X2,…, Xn) and denote its pattern imply as M(X1, X2,…, Xn). Because the pattern imply is the middle of stability for the factors in our pattern, it needs to be intuitively clear that including a brand new statement can destroy this stability. Solely in a single case, just one new quantity Xnew within the pattern (X1, X2,…, Xn, Xnew) is not going to disturb this stability and won’t change the worth of the pattern imply M(X1, X2,…, Xn), and this new quantity is the pattern imply, i.e. Xnew=M(X1, X2,…, Xn). In different phrases, if Xnew=M(X1, X2,…, Xn) then M(X1, X2,…, Xn, Xnew)=M(X1, X2,…, Xn). Or equivalently we will say, if after the enlarging of our pattern (X1, X2,…, Xn) by a brand new worth Xnew to the brand new pattern (X1, X2,…, Xn, Xnew) we nonetheless have the identical pattern imply, i.e. M(X1, X2,…, Xn, Xnew)=M(X1, X2,…, Xn), then that new statement needed to be Xnew=M(X1, X2,…, Xn), please see the determine beneath.

In fact, such property may very well be derived from the corresponding equation:

You are able to do the calculation above and verify if that’s true, but when one understands the pattern imply as a middle of stability such property is simple.
3. A number of factors don’t have an effect on the pattern imply.
The earlier property we will simply generalize for multiple new statement in our pattern. Allow us to assume, that we enlarge our pattern by two new observations. Now the query is when these two new observations don’t change the pattern imply, don’t change our heart of stability. Such a situation is feasible solely when these two new factors are symmetrically positioned across the imply. So, if we have now our pattern (X1, X2, …, Xn) and its pattern imply M(X1, X2, …, Xn) then two new observations Xnew1 and Xnew2 don’t change the pattern imply M(X1, X2,…, Xn, Xnew1, Xnew2) of the enlarged pattern (X1, X2,…, Xn, Xnew1, Xnew2) if and provided that Xnew1 = M(X1, X2, …, Xn)-x and Xnew2 = M(X1, X2, …, Xn)+x, for some x, please see the determine beneath.
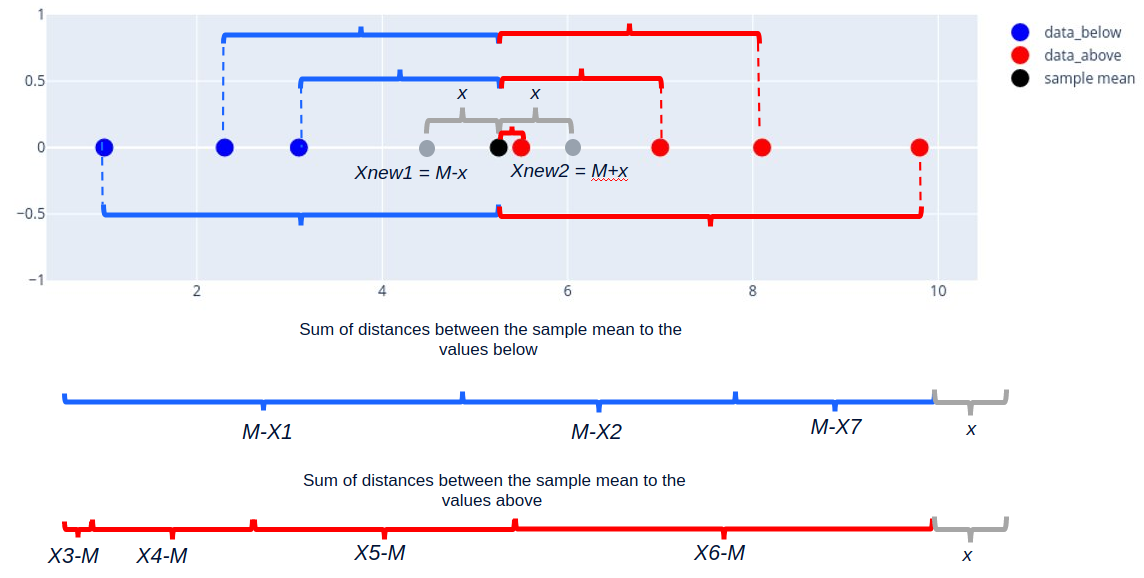
Once more, this property we will derive utilizing equations and technical transformations:
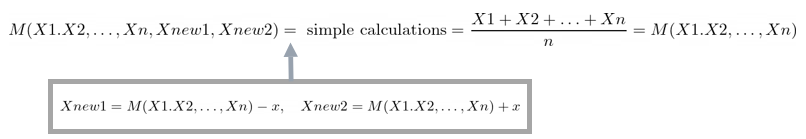
So, the conclusion is that the new observations symmetrically positioned across the pattern imply don’t change the pattern imply.
4. Outlier influence.
The influence of 1 statement on the pattern imply may very well be of any dimension. Intimately, if we shift some statement Xn in our pattern (X1, X2, …, Xn) by some x (so we modify Xn to Xn+x) then the pattern imply shifts by x/n, i.e. M(X1, X2, …, Xn+x)=M(X1, X2, …, Xn)+x/n, mathematically:

Allow us to take a look at our exemplary pattern within the determine beneath.
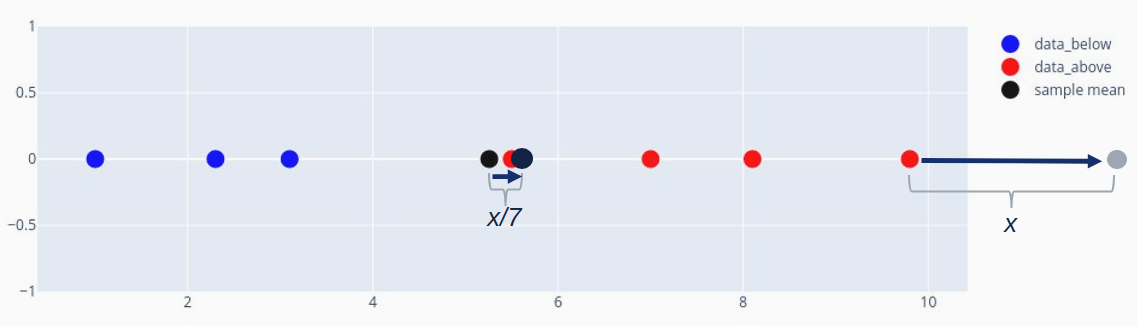
Due to this fact, we see that the influence of an outlier on the pattern imply may very well be extraordinarily huge and of any dimension. Mathematically, we will write that:


