A step-by-step differentiation of the Sigmoid activation and cross-entropy loss perform
This text will undergo step-by-step differentiation of Sigmoid and Cross-Entropy capabilities. The understanding of derivatives of those two capabilities is crucial within the space of machine studying when performing back-propagation throughout mannequin coaching.
Sigmoid/ Logistic perform is outlined as:

The place is e is the Euler’s quantity — a transcendental fixed roughly equal to 2.718281828459. For any worth of x, the Sigmoid perform g(x) falls within the vary (0, 1). As a worth of x decreases, g(x) approaches 0, whereas as x grows larger, g(x) tends to 1. Examples,

From right here, we are going to now differentiate the Sigmoid perform utilizing two strategies — Quotient and chain guidelines of differentiation.
Spinoff of Sigmoid Operate utilizing Quotient Rule
Step 1: Stating the Quotient Rule

The quotient rule is learn as “the by-product of a quotient is the denominator multiplied by by-product of the numerator subtract the numerator multiplied by the by-product of the denominator all the things divided by the sq. of the denominator.”
Step 2: Apply the Quotient rule
From the Sigmoid perform, g(x) and the quotient rule, now we have

Two issues to notice:
- The by-product of of a continuing is equals to zero. That’s the reason
u’=0. - The differentiation of exponential perform (
e*) invis roofed by Exponential rule of differentiation.

By quotient and exponential rule of differentiation, now we have

That’s the by-product of a Sigmoid perform however we are able to simplify additional as proven within the subsequent step.
Step 3: Simplifying the by-product
On this step, we are going to use some ideas on algebra to simplify the by-product end in Step 2.

Be aware: In Equation 5, we added 1 and subtracted 1 to the equation so we truly modified nothing.
That marks the top of the differentiation course of utilizing quotient rule.
Differentiating Sigmoid Operate utilizing Chain Rule
Step 1: The chain rule

Step 2: Rewrite the Sigmoid perform as a damaging exponent

Step 3: Making use of chain rule to Sigmoid perform in Step 2
Let,

Then, by chain rule, we are going to proceed as follows,

At this level, you’ll be able to proceed to simplify the equation utilizing the identical steps we took once we labored on quotient rule (Equations 3 via 8).
Here’s a plot of Sigmoid perform and its by-product

Cross-Entropy loss perform is an important value perform used for classification issues. On this publish, nonetheless, we are going to focus solely on differentiating the loss perform. Nonetheless, you’ll be able to learn extra about Cross-Entropy loss perform within the hyperlink given under
Cross-Entropy loss perform is outlined as:

the place tᵢ is the reality worth and pᵢ is the chance of the iᵗʰ class.
For classification with two lessons, now we have binary cross-entropy loss which is outlined as follows

Spinoff of binary cross-entropy perform
The reality label, t, on the binary loss is a recognized worth, whereas yhat is a variable. Which means the perform might be differentiated with respect to yhat and deal with t as a continuing. Let’s go forward and work on the by-product now.
Step 1: Stating two guidelines we have to differentiate binary cross-entropy loss
To distinguish the binary cross-entropy loss, we’d like these two guidelines:


and the product rule reads, “the by-product of a product of two capabilities is the primary perform multiplied by the by-product of the second plus the second perform multiplied by the by-product of the primary perform.”
Step 2: Differentiating the perform
We’ll use the product rule to work on the derivatives of the 2 phrases individually; then, by Rule 1 we are going to mix the 2 derivatives.
Since now we have two unknowns — t and yhat — we are going to truly work on partial by-product (a partial by-product of a perform of a number of variables is its by-product with respect to one of many variables, with the opposite variables considered fixed).
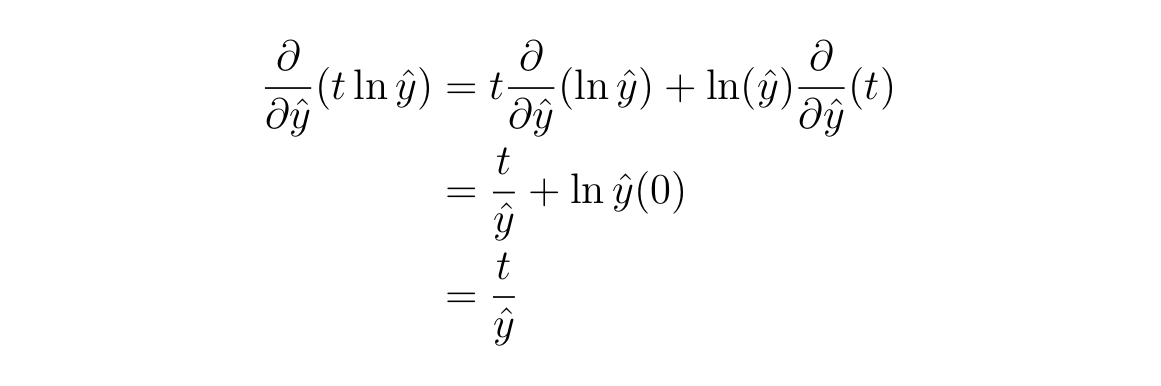

And due to this fact, the by-product of the binary cross-entropy loss perform turns into

That marks the top of this text. Thanks for studying
On this article, we labored on the derivatives of the Sigmoid perform and binary cross-entropy perform. The previous is used primarily in machine studying as an activation perform, whereas the latter is usually used as a value perform to guage fashions. The derivatives discovered listed here are particularly elementary throughout a community’s back-propagation course of — a necessary step throughout mannequin coaching.


