Inference for Runge-Kutta integration with Pymc3

Machine studying strategies have performed an important function in epidemiology analysis. Knowledge scientists on this area are fortunate since they by no means must seek for a data-driven resolution from scratch. Quite the opposite, they are going to be guided by some well-studied mathematical fashions.
This publish explains the right way to use Pymc3, a Python package deal for Bayesian statistical modeling, to construct a bayesian inference to foretell the illness unfold knowledgeable by probably the most primary epidemiological mannequin, for instance, a SIR mannequin. The implementation may also be completed by TensorFlow chance with the same implementation. Please test the pocket book for full python codes.
SIR mannequin might be the best compartmental mannequin and lots of variations derive from it. It describes the dynamics of three primary compartments in the entire inhabitants: inclined people, infectious people, and eliminated people, because the title of the mannequin signifies. The mannequin deserves its chapter and this publish wouldn’t go deep into the small print effectively defined in varied references. As a substitute, we are going to solely give a quick introduction on this part.
The SIR mannequin offers the dynamics of the totally different inhabitants teams with an extraordinary differential equation (ODE), assuming that the entire inhabitants is a continuing N, ignoring the start and demise charge throughout the epidemic.
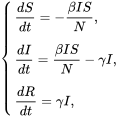
The 2 parameters beta and gamma stand for an infection charge and removing charge. Their ratio is the fundamental copy quantity whose worth determines the asymptotic habits of the epidemic. The dynamics of the epidemics described by the SIR mannequin will probably be decided as soon as the 2 parameters are given.
The dataset used within the following modelization is an artificial dataset generated from a easy simulation with the SIR mannequin. It comprises the populations of the inclined people, infectious people, and eliminated people throughout the first 30 days of an epidemic. The entire inhabitants is 10000 and there have been 10 infectious folks, 9990 inclined folks, and 0 eliminated folks initially. We wish to prepare a mannequin and predict the epidemic within the subsequent 30 days.
To indicate the ability of the next modelization, solely 100 knowledge factors are thought-about.

Aim of modelization
The compartmental mannequin ought to information the machine studying technique to mannequin the event of epidemics. Furthermore, with a given preliminary state, the long run populations of SIR teams could be obtained if we all know the values of beta and gamma. Due to this fact, the primary objective of the modelization turns into to study the 2 parameters of the SIR mannequin.
On the similar time, uncertainty is inevitable once we file totally different teams’ populations. We might subsequently construct a community of the SIR dynamic and Bayesian inference to study the posterior of the 2 regarding parameters.
Runge-Kutta technique
Given by an ODE, the SIR mannequin ought to be discretized earlier than being put into the community. Right here, we are going to use the basic fourth-order Runge-Kutta integration, a numerical technique involving successive approximations for the decision of differential equations with the type of dy/dx=f(x,y).

Inference
- Set the priors of beta and gamma as uniform distributions in [0,1];
- With the given preliminary state of SIR (denoted by y_0), use the Runge-Kutta technique to acquire the sequence of states at future cases.
- Add every occasion a term-wise Poisson noise.
- Do Bayesian inference to get the posterior of beta and gamma.
We won’t present detailed code on this publish. Readers are invited to learn the pocket book and all questions are welcome.
Skilled on the 100 knowledge factors, parameters converge to regular distributions centered at 0.6 and 0.3.

We might thus predict the SIR inhabitants within the following 30 days. We will see within the plot that the epidemic tends to equilibrium asymptotically. Fortuitously, we see virtually no extra new instances ultimately.

On this publish, we plugged a mathematical mannequin right into a bayesian inference and utilized it to the infectious illness unfold use case. A small dataset appears to be adequate for the convergence of parameters when the mannequin is knowledgeable by some background information.
Lastly, we might to comment that the artificial dataset is simply a great case with some unreal simplifications. An attention-grabbing subsequent step could be testing the mannequin on an actual dataset, e.g. covid instances in large cities.


