From a theoretical introduction to the hands-on implementation: right here’s what you want to know concerning the Chirplet Rework

One of the widespread operations of Sign Processing is to remodel the sign. The explanation why we do that’s that it’s not at all times true that the best solution to carry out operations in your sign is by taking a look at it and analyzing it in its pure area*.
* I’ll discuss with the pure area as the unique area of the sign. For instance, if the sign is a time sequence, the pure area is the 2D one the place the x is the time and the y is the sign worth
Let me offer you an instance. Take into account the next sign in its pure area (time sequence):

An attention-grabbing factor to do within the exploration of the sign is to see if the sign may be decomposed right into a sum of elements. The explanation why it’s attention-grabbing to see that’s that it is likely to be attainable that every part has a particular supply. In different phrases, we’re in a roundabout way reverse engineering the sign.
To separate the sign that’s proven above into a number of elements, we have now to alter the area of the sign. That signifies that we have now to have a look at the sign, relatively than within the time area, within the frequency one (extra about it right here).
What we’re suggesting right here is that the sign is a sum of sinusoidal elements. Every part has a particular amplitude, part, and frequency. To investigate that, we use the Fourier Rework.
Within the instance that we’re doing, it seems like this:
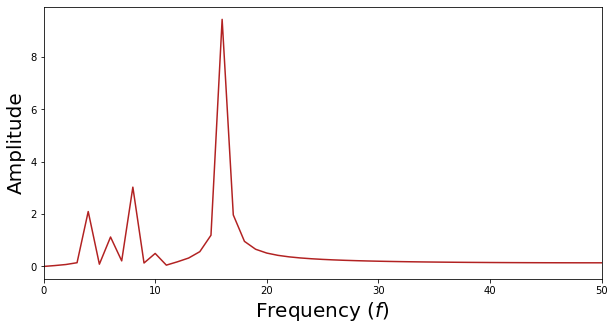
Now if you happen to have a look at the picture above (the so-called spectrum) you see that it has 4 peaks:

Let’s retailer these 4 x-axis values and their correspondent y values in two lists:

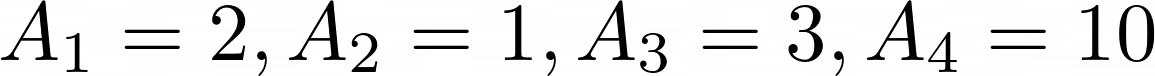
Now, the unique sign may be decomposed into n_c=4 elements. Every part is a sine* with a given amplitude and frequency. We name every one of many elements phi and we name the time array t. Right here is the end result

* It may be a cosine as effectively, I thought of the sine solely to make the instance simpler to understand.
So if we plot these we get:

Fairly dope proper?
Fourier remodel (or relatively its sensible implementation often known as Quick Fourier Rework, which is extremely environment friendly) is each a theoretically attention-grabbing and a really helpful algorithm in sign processing. We use that in Picture Processing, Audio Processing, Time Collection Evaluation, and quite a lot of different fields. Nonetheless, amongst all of the assumptions this algorithm makes there’s a fairly large one:
The Fourier Rework considers the frequencies to be mounted with respect to time.
And this isn’t at all times true.
For instance, have a look (or really a pay attention) to the next sound: https://www.youtube.com/watch?v=5TGCFGsQIx0
You hearken to a low be aware (low pitch) firstly that begins to get greater and better to some extent that it’s virtually annoying. In that case, the sine wave seems like this:

At this level, if you happen to attempt to apply the Fourier Rework of this sign, it wouldn’t make any sense, since you are counting on an assumption that’s not true: the frequency does change with time!
The type of sinusoidal waves that change with time is normally known as chirp. The way in which to acquire a decomposition of a sign that’s fabricated from chirp is known as chirplet remodel.
Let’s get began!
The equation of the Chirplet Rework is the next:

Let me describe all of the values that you just see within the equation above:
1.1 Beta
The Beta worth is the amplitude of a Chirplet. It’s the solely worth that’s not the argument of the exponential operate:


If you happen to have a look at the picture above, fixing all of the values, the beta solely modifications the amplitude.
1.2 Alpha 1
The alpha_1 bit is the one one that’s not sinusoidal. If you happen to have a look at the expression above is nothing however a gaussian time period.


Particularly, the alpha_1 time period is the variance of the Gaussian. Which means the smaller alpha_1 is, the broader it’s the form of your bell. This time period is often known as the modulation time period.
1.3 f_c
f_c is the sinusoidal time period. Bear in mind! We’re choosing solely the true half, so it’s nothing however a sinusoidal a part of our chirplet.


The most important the f_c worth, the extra ups and downs you see in the identical period of time (on this case, 500 knowledge factors)
1.4 Alpha_2
alpha_2 is the pure chirp half. What I imply is that this part goes up and down with time, and it has the habits we plotted and noticed earlier than with the YouTube video.


As you possibly can see, the variety of ups and downs will increase (equally to what occurs in f_c), however right here the quantity just isn’t mounted, however it will increase with time.
1.5 Phi
The phi parameter is fairly straightforward to grasp. It’s nothing however a part shift. As we are able to see, it’s the solely parameter that’s within the argument of an exponential however with no time dependency. This solely brings a change of part in our sinusoidal waves. For instance, if we take into account this part shift with the sine half (the one associated to alpha1) we get:


1.6 tau
The tau parameter might be the best one. All of the chirplet operate is an exponential of some form (imaginary or not) and it’s centered round a time worth. That point worth is tau.


In these few strains of code you possibly can:
A. Generate a chirplet
B. Play with the parameters above and see the variations
C. Plot the outcomes
2.1 Analytical Perform Definition:
2.2 Producing a default chirplet:
2.3 Producing a random chirplet:
2.4 Plotting a random chirplet:
If you happen to favored the article and also you need to know extra about Machine Studying, otherwise you simply need to ask me one thing you possibly can:
A. Observe me on Linkedin, the place I publish all my tales
B. Subscribe to my publication. It can maintain you up to date about new tales and provide the likelihood to textual content me to obtain all of the corrections or doubts you might have.
C. Grow to be a referred member, so that you received’t have any “most variety of tales for the month” and you’ll learn no matter I (and 1000’s of different Machine Studying and Information Science prime writers) write concerning the latest expertise accessible.



