A Markov Resolution Course of is without doubt one of the most basic data in Reinforcement Studying. It’s used to signify determination making in optimization issues.
The model we current right here is the Finite MDP, which analyses discrete time, with discrete motion issues, with some quantity of stochasticity concerned. This implies the identical sequence of actions has a likelihood to result in a special state of affairs between two tries.
Right here, we concentrate on the presenting a basic construction of the mathematical framework, akin to the weather concerned and the equations linking them collectively. We’ll additionally cowl some difficulties we would encounter when formulating an issue as an MDP.
Your studying system is usually known as an agent, in most trendy literature. This time period contains extra than simply the neural community estimator in latest algorithms. The agent interacts with an atmosphere to unravel a activity. We’ll go into additional particulars later into what constitutes the atmosphere, as it may turn out to be problematic. The atmosphere depends on two important elements: its transition and reward capabilities. Each are linked to the character of the system and of the duty.
For instance, the next graph represents an atmosphere with three states and 4 actions accessible to an agent. The duty the agent should accomplish is transitioning all three states and coming again. There are states with constructive and destructive rewards, which may correspond to marginal achieve or detrimental side-goals. This view is from an exterior, all-powerful observer, that may see the issue as an entire. That is typically not the case for our brokers, that may solely observe what’s round them and the results of their direct actions.
Query: Are you able to remedy the anticipated returns from the primary state, utilizing a random coverage? If sure, reply! Such a coverage would have an equal probability to choose both motion 0 or 1 at any state. Keep tuned to an article on worth capabilities!
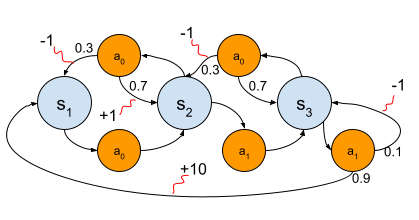
The graph illustration is a visible synthesis of the MDP, expressed as a tuple:
The place:
- S is the set of all states reachable by the agent. They’re the blue nodes within the earlier graph.
- A is the set of actions, known as the motion area. That is typically conditioned by the state s in S, which means the actions accessible in that state s. They’re the orange nodes within the earlier graph.
- P is the transition likelihood matrix. It corresponds to the chances that an motion a will transition state s to state s’. They’re the chances famous after some actions within the earlier graph, akin to 0.6 to transition from state 2 to state 1 after utilizing motion 1.
- R is the speedy reward ensuing from a transition between s and s’. They’re denoted by integers pointed to by a pink squiggle.
Whereas the graph is a illustration of the entire system, if we wish to analyse an agent’s expertise, we should describe every determination inside its context. This context is usually inside an episode, a finite sequence from t=0 to T.
The size of an episode is usually outlined by the duty, akin to fixing a maze in Y strikes. However, some issues are doubtlessly infinite, with no tractable finish in sight, akin to in monetary buying and selling or low-level robotics. On this case, an episode’s finish is outlined artificially, and the agent learns on a section of the expertise.

Every interplay is outlined because the tuple:
From the present state s, the agent chooses motion a, which ends up in the brand new state s’, with the reward r. The motion was chosen primarily based on a coverage π, the principle part your studying algorithm is attempting to optimize in any method of RL.
The coverage π is a mapping between a state illustration and actions. We’ve got an identical habits, as people: when going dwelling, we all know to show left on a particular intersection, or to hit the brakes when a visitors gentle turns pink. We acknowledge patterns and know which actions match them.
However, to acknowledge one thing, it wants a definite form, which permits us to make the proper choices. If all of the corridors in a constructing had been precisely the identical, with no signage, would you be capable to discover your manner round utilizing solely what your eyes noticed at a given second?
The principle objective of a state illustration is giving an agent sufficient data for it to know which state it’s in and the place it ought to go subsequent. These may embody sensor readings, photographs or processed indicators.
In duties the place solely observations are wanted, akin to for a robotic arm choosing up an object, solely the sensors are required. If we all know the place the arm and the thing are, we are able to predict increments for the rotors.
In duties that require some notion of historical past, processed indicators are obligatory. In a self-driving automobile, sensing the place of a automobile is as vital as understanding *the place* that automobile goes.
In each circumstances, the right granularity of knowledge is vital. Any granularity appropriate for the duty can be utilized, from the bottom sensors to the best abstraction stage.
Telling a robotic arm that it should go “left”, when it controls rotors, is probably not sufficient: how far should it go? 1 increment, 1 / 4 flip or a full flip? It should be tailored to every activity, to facilitate the agent’s studying.
As such, a controller agent could also be skilled to offer out high-order actions, akin to “left, proper, down, up”, {that a} driving agent might interpret as enter. This driving agent will then, in flip, act upon rotors utilizing low-level actions akin to voltage or increments.
Robotics issues spotlight one other preoccupation: the place will we outline the break up between an agent’s properties and the atmosphere? Absolutely the place of an arm in an area or the quantity of inventory in stock offers brokers vital details about the atmosphere, however are linked to their actions, which needs to be a part of the agent and never the atmosphere.
But, they’re the outcomes of the actions, both from making use of a voltage to motors or from shopping for gadgets. The restrict between the agent and the atmosphere are the variables instantly underneath management of the agent. As such, the final voltage utilized shouldn’t be thought of a part of the atmosphere, however as a part of the agent.
The aim of an agent is to maximise the anticipated rewards from a sequence of actions. Because the anticipated rewards are the cumulative rating achieved by means of an entire episode, the agent might make domestically sub-optimal selections, as a way to attain extra worthwhile outcomes in a while. That is most evident within the sport of chess, the place gamers are keen to sacrifice items, if it results in a good place. What is taken into account favorable or in any other case is outlined by the reward operate.
Rewards
A reward is given for particular state-transitions. They are often reached both at each step or on the finish of an episode. Since an agent tries to maximise them, correctly shaping a reward operate can affect the specified habits we want to see an agent show. It may be any worth operate so long as it highlights the specified finish aim.
- For duties with clear end-goals, a big reward will be given when it’s reached.
- For video video games, the in-game rating will be exploited.
- But for robotics duties with security preoccupations, we additionally want a method to discourage harmful habits.
- If the security of people is in danger, ending an episode early with a big destructive reward ensures the agent shortly steers away from these actions.
- For much less extreme circumstances, destructive rewards make sure that the agent doesn’t dwell in that state.
Rewards can embody a mix of various capabilities so long as it respects basic metrics tips. As such, it needs to be convex, in order that given an order, you’ll be able to rank performances utilizing that order. If a better rating is best, there shouldn’t be any circumstances the place a decrease rating reaches a greater rating.
Lastly, whereas utilizing composite capabilities, they need to all be on the identical order of magnitudes or the decrease order capabilities will hardly ever be taken under consideration.
Returns
We outline the returns G because the cumulative rewards which our agent receives throughout an episode:
In lots of RL issues, the size of episodes are fairly lengthy. As such, the primary steps in an episode might have complicated anticipated returns, with no clear actions to make. One resolution was to introduce a discounting issue. It narrows how far forward an agent estimates the rewards it may attain. Our return G turns into:
As we are able to see, deciding on a correct γ signifies that steps additional out contribute near nothing to an actions’ returns:
Due to this fact, the anticipated returns from a given time inside an episode will be obtained from:
For reference, here’s a scale of how far forward the agent can look primarily based on γ:
- 0.9 = 10 steps
- 0.99 = 100 steps
- 0.999 = 1000 steps
From earlier sections, we have now seen the transition likelihood matrix, and the right way to compute the anticipated returns from an episode. These notions are the premise that enable us to conceive the constructing blocks of a choice making course of!
We will estimate the returns we are able to attain by utilizing any motion in our present state:
The present state s is fastened, so we are able to iterate all of the actions a accessible in s. For every motion, we estimate the likelihood of touchdown in state s’, which ought to reward us with a rating r. In lots of issues, the operate Pr is understood, however for others, it’s estimated utilizing strategies akin to Monte Carlo Sampling.
From this equation, we are able to additionally disregard the rewards and concentrate on the state-transition possibilities, the place we’re prone to go subsequent:
To acquire solely the anticipated returns, for every path accessible to the agent in its state, we use the “state — motion — subsequent state” estimated returns:
This usually requires greater than the speedy sensations, however by no means greater than the entire historical past of all previous sensations. From Sutton and Barto, 2018.
The Markovian Property is a requirement for what’s included within the state sign, which completes what was talked about within the “Representing the System” part.
The data should solely comprise a way of speedy measurements. Protecting all previous observations is extremely discouraged because of the intractability of such a follow. However, a way of previous actions, akin to to spotlight motion in an autonomous automobile system, is feasible. The thought is to maintain the image as gentle as doable to facilitate studying a coverage π.
This property is required as a result of the mathematical framework assumes that the following state s’ is instantly linked to the present state s and the motion a that was chosen. If this relation will not be true, the principle equations fail and studying turns into unlikely.
Nevertheless, completely Markovian issues are uncommon in the actual world, which is why some tolerance is accepted, and newer frameworks, together with Partially Summary MDP and Partially Observable MDP (POMDP), had been introduced lately.
These have allowed us to mannequin issues together with Poker, which is legendary for being an incomplete downside, the place every participant has no details about its opponent’s hand. It is usually made extra complicated by the psychology concerned within the sport. A participant could also be recognized to bluff often, or to fold when not sure.
Thus, Poker requires data which isn’t accessible within the direct atmosphere, and due to this fact contradicts the Markovian Property. But, we have now seen some latest outcomes of Deep Reinforcement Studying brokers beating Human Poker gamers. This is dependent upon framing the issue and discovering a method to convey sufficient data to the agent.

