Are you continue to confused in regards to the working of SHAP and Shapley values? Let me present the most straightforward and intuitive clarification of SHAP and Shapley values on this article.

SHapley Additive exPlanation (SHAP), which is one other widespread Explainable AI (XAI) framework that may present model-agnostic native explainability for tabular, picture, and textual content datasets.
SHAP relies on Shapley values, which is an idea popularly utilized in Sport Concept. Though the mathematical understanding of Shapley values may be difficult, I’ll present a easy, intuitive understanding of Shapley values and SHAP and focus extra on the sensible features of the framework.
The SHAP framework was launched by Scott Lundberg and Su-In Lee of their analysis work, A Unified Method of Deciphering Mannequin Predictions. This was printed in 2017. SHAP relies on the idea of Shapley values from cooperative sport principle, it considers additive function significance.
By definition, the Shapley worth is the imply marginal contribution of every function worth throughout all potential values within the function area. The mathematical understanding of Shapley values is difficult and would possibly confuse most readers. That mentioned, if you’re desirous about getting an in-depth mathematical understanding of Shapley values, we advocate that you simply check out the analysis paper known as “A Worth for n-Individual Video games.” Contributions to the Concept of Video games 2.28 (1953), by Lloyd S. Shapley. Within the subsequent part, we are going to acquire an intuitive understanding of Shapley values with a quite simple instance.
On this part, I’ll clarify Shapley values utilizing a quite simple and easy-to-understand instance. Let’s suppose that Alice, Bob, and Charlie are three buddies who’re participating, as a staff, in a Kaggle competitors to unravel a given drawback with ML, for a sure money prize. Their collective aim is to win the competitors and get the prize cash. All three of them are equally not good in all areas of ML and, due to this fact, have contributed in numerous methods. Now, in the event that they win the competitors and earn their prize cash, how will they guarantee a good distribution of the prize cash contemplating their particular person contributions? How will they measure their particular person contributions for a similar aim? The reply to those questions may be given by Shapley values, which had been launched in 1951 by Lloyd Shapley.
The next diagram provides us a visible illustration of the situation:

So, on this situation, Alice, Bob, and Charlie are a part of the identical staff, taking part in the identical sport (which is the Kaggle competitors). In sport principle, that is known as a Coalition Sport. The prize cash for the competitors is their payout. So, Shapley values inform us the typical contribution of every participant to the payout making certain a good distribution. However why not simply equally distribute the prize cash between all of the gamers? Effectively, because the contributions usually are not equal, it’s not honest to distribute the cash equally.
Now, how can we resolve the fairest method to distribute the payout? A method is to imagine that Alice, Bob, and Charlie joined the sport in a sequence by which Alice began first, adopted by Bob, after which adopted by Charlie. Let’s suppose that if Alice, Bob, and Charlie had participated alone, they’d have gained 10 factors, 20 factors, and 25 factors, respectively. But when solely Alice and Bob teamed up, they may have obtained 40 factors. Whereas Alice and Charlie collectively may get 30 factors, Bob and Charlie collectively may get 50 factors. When all three of them collaborate collectively, solely then do they get 90 factors, which is ample for them to win the competitors.

Mathematically, if we assume that there are N gamers, the place S is the coalition subset of gamers and 𝑣(𝑆) is the entire worth of S gamers, then by the system of Shapley values, the marginal contribution of participant i is given as follows:

The equation of Shapley worth would possibly look difficult, however let’s simplify this with our instance. Please observe that the order by which every participant begins the sport is essential to think about as Shapley values attempt to account for the order of every participant to calculate the marginal contribution.
Now, for our instance, the contribution of Alice may be calculated by calculating the distinction that Alice may cause to the ultimate rating. So, the contribution is calculated by taking the distinction within the factors scored when Alice is within the sport and when she is just not.
Additionally, when Alice is taking part in, she will be able to both play alone or staff up with others. When Alice is taking part in, the worth that she will be able to create may be represented as 𝑣(𝐴). Likewise, 𝑣(𝐵) and 𝑣(𝐶) denote particular person values created by Bob and Charlie. Now, when Alice and Bob are teaming up, we are able to calculate solely Alice’s contribution by eradicating Bob’s contribution from the general contribution. This may be represented as 𝑣(𝐴, 𝐵)– 𝑣(𝐵) . And if all three are taking part in collectively, Alice’s contribution is given as 𝑣(𝐴, 𝐵, 𝐶)– 𝑣(𝐵, 𝐶).
Contemplating all potential permutations of the sequences by which Alice, Bob, and Charlie play the sport, the marginal contribution of Alice is the typical of her particular person contributions in all potential situations.

So, the general contribution of Alice shall be her marginal contribution throughout all potential situations, which additionally occurs to be the Shapley worth. For Alice, the Shapley worth is 20.83. Equally, we are able to calculate the marginal contribution for Bob and Charlie, as proven within the following desk:
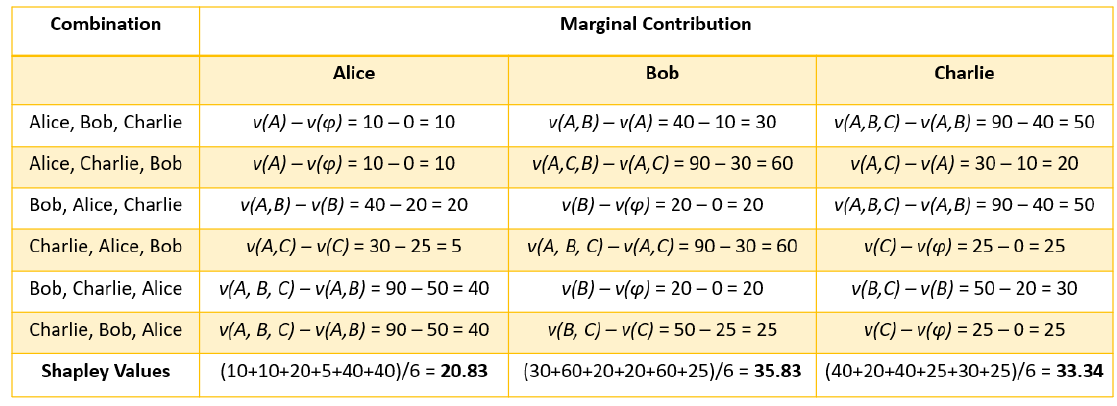
I hope this wasn’t too obscure! One factor to notice is that the sum of marginal contributions of Alice, Bob, and Charlie needs to be equal to the entire contribution made by all three of them collectively. Now, let’s attempt to perceive Shapley values within the context of ML.
To be able to perceive the significance of Shapley values in ML to elucidate mannequin predictions, we are going to attempt to modify the instance about Alice, Bob, and Charlie that we used for understanding Shapley values. We are able to think about Alice, Bob, and Charlie to be three totally different options current in a dataset used for coaching a mannequin. So, on this case, the participant contributions would be the contribution of every function. The sport or the Kaggle competitors would be the black-box ML mannequin and the payout would be the prediction. So, if we need to know the contribution of every function towards the mannequin prediction, we are going to use Shapley values.

Due to this fact, Shapley values assist us to know the collective contribution of every function towards the result predicted by black-box ML fashions. Through the use of Shapley values, we are able to clarify the working of black-box fashions by estimating the function contributions.
On this article, we centered on understanding the significance of the SHAP framework for mannequin explainability. By now, you have got a superb understanding of Shapley values and SHAP.
- GitHub repo for Python SHAP framework — https://github.com/slundberg/shap
- Utilized Machine Studying Explainability Strategies — https://amzn.to/3cY4c2h


