Leveraging linear regression for characteristic choice of steady/categorical variables

Linear regression is among the many main/entry-level Machine Studying (ML) fashions. It owes that to its…
- Simplicity: It fashions a given response y as a linear mixture of some variables x_1, …, x_p
- Interpretability: The coefficient related to variable x_j hints at its relationship with the response y
- Trainability: It does not require a variety of hyperparameter tuning throughout coaching.
It’s not even unsuitable to say that it’s the synonym of the “Hey world” program for Knowledge scientists. Regardless of being fundamental, linear regression nonetheless has another fairly fascinating properties to unfold …
Discovering the linear regression coefficients β_1, …, β_p includes discovering the “finest” linear mixture of variables that approaches the response. Stated otherwise, discovering the coefficients that decrease the imply squared error (MSE).
It’s doable to endow the regression coefficients with some further properties by contemplating the MSE plus a further penalty time period.

It’s just like implicitly saying to the mannequin: retain as a lot knowledge constancy as doable whereas making an allowance for the penalty time period with depth α. It occurs that with a selected alternative of the penalty time period, we are able to present linear regression with a characteristic choice property.
Lasso characteristic choice works properly till you take into account categorical variables
After we set the penalty time period because the L1-norm — the sum of absolutely the values of the regression coefficients — we get an answer with few non-zero coefficients. That is identified within the literature because the Lasso mannequin and its ensuing resolution enjoys a characteristic choice property as the (few) non-zero coefficients point out probably the most related options to the mannequin, and subsequently the options to pick.


It is vitally frequent to come across categorical variables — for instance, a variable coloration that takes “pink,” “white,” and “blue” as values. These should be encoded beforehand in a numerical kind for use in a regression mannequin. And to take action, we regularly resort to utilizing one-hot encoding — exploding a variable into its dummy values — to keep away from implicitly implementing an order between the values.
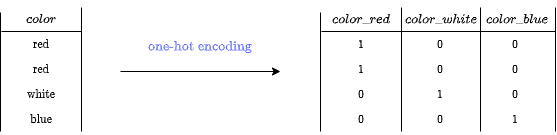
Making use of Lasso on this particular case will not be acceptable as a characteristic choice technic because it treats the variables independently and therefore ignores any relationship between them, in our case, it disregards the truth that the dummy variables, taken as an entire, characterize the identical categorical variable.
As an example, if Lasso chosen color_red amongst color_white and color_blue, then it does not say a lot in regards to the relevance of the “coloration” variable.
Group Lasso for a combination of steady/categorical characteristic choice
Ideally, we want a penalty that considers the dummies of a categorical variable as an entire, in different phrases, a penalty that includes the underlying “group construction” between the dummies when coping with categorical variables.
This may be achieved by extending Lasso by barely altering its penalty to deal with teams of variables. To take action, we rearrange the regression coefficients that belong to the identical group in vectors. Then, we take into account the sum of their L2-norm.


The ensuing mannequin is thought within the literature as Group Lasso. It’s value mentioning that by contemplating the above penalty we obtained a mannequin that:
- has a group-wise characteristic choice property. The variables of a bunch are both all chosen (assigned non-zero coefficients) or expelled (assigned zero coefficients).
- treats equally the variables of a bunch. We’re utilizing the L2-norm which is thought to be isotropic and therefore gained’t privilege any of the variables of a bunch — in our case, the dummies of a categorical variable.
- handles a combination of single and group variables. The L2-norm in a one-dimensional area is absolutely the worth. Due to this fact, Group Lasso reduces to Lasso if the teams consist of 1 variable.

Based mostly on that, we are able to use Group Lasso to carry out characteristic choice of a combination of steady/categorical variables. Steady variables shall be thought-about as teams with one variable and categorical ones shall be handled as teams of dummies.
scikit-learn is among the well-known python packages which can be behind the prevalence of ML these days. Its user-friendly API and complete documentation lowered the boundaries to entry to the ML area and enabled non-practitioners to learn from it with out bother.

Sadly, Group Lasso is lacking from scikit-learn implementation. But, that’s not stunning in any respect, as numerous are right this moment’s ML fashions, not to mention when you think about their variants!
Probably, there are a number of initiatives that purpose at preserving ML accessible to most of the people by standardizing the implementation of ML fashions and aligning them with scikit-learn API.
celer: a scikit-learn API conform package deal for Lasso-like fashions
celer is a python package deal that embraces the scikit-learn imaginative and prescient and offers fashions which can be solely designed below scikit-learn API and thereby combine properly with it — can be utilized with Pipelines, and GridSearchCV amongst others. Therefore, becoming one in every of celer‘s fashions is as easy as doing the identical for scikit-learn.
Additionally, celer is specifically designed to deal with Lasso-like fashions reminiscent of Lasso and Group Lasso. Due to this fact, it encompasses a tailor-made implementation that allows it to suit most of these fashions shortly — as much as 100 instances quicker than scikit-learn — and effectively on massive datasets.
Getting began with celer Group Lasso
After putting in celer by way of pip, you possibly can simply match a Group Lasso mannequin as proven within the snippet beneath. Right here, a toy dataset with one steady variable and two categorical variables is taken into account.
Now we have efficiently fitted a Group Lasso and henceforth all that continues to be is to examine the ensuing resolution — non-zero coefficients — to resolve on the variables to pick.
Ideally in characteristic choice, we’re slightly excited about answering the query: what are the highest Okay’s most related options? Due to this fact we are able to’t declare that we 100% answered this query because the non-zero coefficients — variables to pick — is determined by the depth of the penalty α and therefore we don’t have full management over them.
The extra we improve α from 0 — pure linear regression — the extra variables are filtered out — assigned zero coefficients. Finally, for a “massive sufficient” α we get a zero resolution — all coefficients are zeros.
Because of this the extra a variable “survives” being expelled by a excessive α, the extra it exhibits its significance to the mannequin. Due to this fact, we are able to depend on the penalty depth to attain the variables.
Apparently, given a response and a group of variables, we are able to present that there exists an α_max above which the zero resolution is the one resolution that trades off knowledge constancy and the penalty.

This means that each variable would have a finite rating between 0 and α_max. Moreover, since we’ve got an specific method of α_max, we are able to additional normalize the scores by α_max to acquire scores between 0 and 1 as an alternative.
To sum up the strategy, we first generate a grid of α between 0 and α_max. Then, we match Group Lasso on every of these α and observe when the variables are assigned zero coefficients — it is going to be their corresponding rating. Lastly, we normalize these scores and thereafter rank the variables based on them.
All of the above steps, besides the final one, are meticulously dealt with by celer_path — the constructing block of celer fashions.
Again to the unique query: what are the highest Okay’s most related options? All that continues to be is to kind descendingly the options based on their scores and choose the highest Okay ones.

Linear regression stays undoubtedly one of many easiest and easy-to-understand fashions which coupled with well-chosen penalties yields extra interpretable outcomes.
On this article, we prolonged linear regression to carry out characteristic choice of a combination of steady/categorical variables utilizing the Group Lasso mannequin.
Ultimately, we used celer to suit Group Lasso in addition to relied on its core solver — celer_path — to manage the variety of chosen options.
I made an in depth GitHub repository the place I utilized the launched characteristic choice technic to an actual dataset. You possibly can examine the supply code in this hyperlink, and leverage the developed python utils to use it to your individual use case.
helpful hyperlinks:


