This publish discusses probably the most thrilling highlights and most promising instructions in optimization for Deep Studying.
Desk of contents:
Deep Studying finally is about discovering a minimal that generalizes nicely — with bonus factors for locating one quick and reliably. Our workhorse, stochastic gradient descent (SGD), is a 60-year outdated algorithm (Robbins and Monro, 1951) , that’s as important to the present technology of Deep Studying algorithms as back-propagation.
Completely different optimization algorithms have been proposed in recent times, which use totally different equations to replace a mannequin’s parameters. Adam (Kingma and Ba, 2015) was launched in 2015 and is arguably immediately nonetheless probably the most generally used certainly one of these algorithms. This means that from the Machine Studying practitioner’s perspective, finest practices for optimization for Deep Studying have largely remained the identical.
New concepts, nevertheless, have been developed over the course of this 12 months, which can form the best way we are going to optimize our fashions sooner or later. On this weblog publish, I’ll contact on probably the most thrilling highlights and most promising instructions in optimization for Deep Studying in my view. Notice that this weblog publish assumes a familiarity with SGD and with adaptive studying charge strategies akin to Adam. To stand up to hurry, discuss with this weblog publish for an summary of present gradient descent optimization algorithms.
Bettering Adam
Regardless of the obvious supremacy of adaptive studying charge strategies akin to Adam, state-of-the-art outcomes for a lot of duties in pc imaginative and prescient and NLP akin to object recognition (Huang et al., 2017) or machine translation (Wu et al., 2016) have nonetheless been achieved by plain outdated SGD with momentum. Current idea (Wilson et al., 2017) offers some justification for this, suggesting that adaptive studying charge strategies converge to totally different (and fewer optimum) minima than SGD with momentum. It’s empirically proven that the minima discovered by adaptive studying charge strategies carry out usually worse in comparison with these discovered by SGD with momentum on object recognition, character-level language modeling, and constituency parsing. This appears counter-intuitive on condition that Adam comes with good convergence ensures and that its adaptive studying charge ought to give it an edge over the common SGD. Nevertheless, Adam and different adaptive studying charge strategies aren’t with out their very own flaws.
Decoupling weight decay
One issue that partially accounts for Adam’s poor generalization means in contrast with SGD with momentum on some datasets is weight decay. Weight decay is mostly utilized in picture classification issues and decays the weights (theta_t) after each parameter replace by multiplying them by a decay charge (w_t) that’s barely lower than (1):
(theta_{t+1} = w_t : theta_t )
This prevents the weights from rising too massive. As such, weight decay will also be understood as an (ell_2) regularization time period that is dependent upon the load decay charge (w_t) added to the loss:
(mathcal{L}_text{reg} = dfrac{w_t}{2} |theta_t |^2_2 )
Weight decay is often applied in lots of neural community libraries both because the above regularization time period or instantly to change the gradient. Because the gradient is modified in each the momentum and Adam replace equations (through multiplication with different decay phrases), weight decay not equals (ell_2) regularization. Loshchilov and Hutter (2017) thus suggest to decouple weight decay from the gradient replace by including it after the parameter replace as within the unique definition.
The SGD with momentum and weight decay (SGDW) replace then appears to be like like the next:
(
start{align}
start{break up}
v_t &= gamma v_{t-1} + eta g_t
theta_{t+1} &= theta_t – v_t – eta w_t theta_t
finish{break up}
finish{align}
)
the place (eta) is the educational charge and the third time period within the second equation is the decoupled weight decay. Equally, for Adam with weight decay (AdamW) we acquire:
(
start{align}
start{break up}
m_t &= beta_1 m_{t-1} + (1 – beta_1) g_t
v_t &= beta_2 v_{t-1} + (1 – beta_2) g_t^2
hat{m}_t &= dfrac{m_t}{1 – beta^t_1}
hat{v}_t &= dfrac{v_t}{1 – beta^t_2}
theta_{t+1} &= theta_{t} – dfrac{eta}{sqrt{hat{v}_t} + epsilon} hat{m}_t – eta w_t theta_t
finish{break up}
finish{align}
)
the place (m_t) and (hat{m}_t) and (v_t) and (hat{v}_t) are the biased and bias-corrected estimates of the primary and second moments respectively and (beta_1) and (beta_2) are their decay charges, with the identical weight decay time period added to it. The authors present that this considerably improves Adam’s generalization efficiency and permits it to compete with SGD with momentum on picture classification datasets.
As well as, it decouples the selection of the educational charge from the selection of the load decay, which permits higher hyperparameter optimization because the hyperparameters not rely on one another. It additionally separates the implementation of the optimizer from the implementation of the load decay, which contributes to cleaner and extra reusable code (see e.g. the quick.ai AdamW/SGDW implementation).
Fixing the exponential shifting common
A number of latest papers (Dozat and Manning, 2017; Laine and Aila, 2017) , empirically discover {that a} decrease (beta_2) worth, which controls the contribution of the exponential shifting common of previous squared gradients in Adam, e.g. (0.99) or (0.9) vs. the default (0.999) labored higher of their respective functions, indicating that there is likely to be a problem with the exponential shifting common.
An ICLR 2018 submission formalizes this situation and pinpoints the exponential shifting common of previous squared gradients as another excuse for the poor generalization behaviour of adaptive studying charge strategies. Updating the parameters through an exponential shifting common of previous squared gradients is on the coronary heart of adaptive studying charge strategies akin to Adadelta, RMSprop, and Adam. The contribution of the exponential common is well-motivated: It ought to stop the educational charges to turn out to be infinitesimally small as coaching progresses, the important thing flaw of the Adagrad algorithm. Nevertheless, this short-term reminiscence of the gradients turns into an impediment in different situations.
In settings the place Adam converges to a suboptimal resolution, it has been noticed that some minibatches present massive and informative gradients, however as these minibatches solely happen not often, exponential averaging diminishes their affect, which ends up in poor convergence. The authors present an instance for a easy convex optimization drawback the place the identical behaviour may be noticed for Adam.
To repair this behaviour, the authors suggest a brand new algorithm, AMSGrad that makes use of the utmost of previous squared gradients relatively than the exponential common to replace the parameters. The total AMSGrad replace with out bias-corrected estimates may be seen under:
(
start{align}
start{break up}
m_t &= beta_1 m_{t-1} + (1 – beta_1) g_t
v_t &= beta_2 v_{t-1} + (1 – beta_2) g_t^2
hat{v}_t &= textual content{max}(hat{v}_{t-1}, v_t)
theta_{t+1} &= theta_{t} – dfrac{eta}{sqrt{hat{v}_t} + epsilon} m_t
finish{break up}
finish{align}
)
The authors observe improved efficiency in comparison with Adam on small datasets and on CIFAR-10.
Tuning the educational charge
In lots of circumstances, it isn’t our fashions that require enchancment and tuning, however our hyperparameters. Current examples for language modelling display that tuning LSTM parameters (Melis et al., 2017) and regularization parameters (Merity et al., 2017) can yield state-of-the-art outcomes in comparison with extra advanced fashions.
An necessary hyperparameter for optimization in Deep Studying is the educational charge (eta). In actual fact, SGD has been proven to require a studying charge annealing schedule to converge to an excellent minimal within the first place. It’s typically thought that adaptive studying charge strategies akin to Adam are extra sturdy to totally different studying charges, as they replace the educational charge themselves. Even for these strategies, nevertheless, there generally is a massive distinction between an excellent and the optimum studying charge (psst… it is (3e-4)).
Zhang et al. (2017) present that SGD with a tuned studying charge annealing schedule and momentum parameter is just not solely aggressive with Adam, but additionally converges sooner. Alternatively, whereas we would suppose that the adaptivity of Adam’s studying charges may mimic studying charge annealing, an express annealing schedule can nonetheless be useful: If we add SGD-style studying charge annealing to Adam, it converges sooner and outperforms SGD on Machine Translation (Denkowski and Neubig, 2017) .
In actual fact, studying charge annealing schedule engineering appears to be the brand new characteristic engineering as we will typically discover highly-tuned studying charge annealing schedules that enhance the ultimate convergence behaviour of our mannequin. An attention-grabbing instance of that is Vaswani et al. (2017) . Whereas it’s regular to see a mannequin’s hyperparameters being subjected to large-scale hyperparameter optimization, it’s attention-grabbing to see a studying charge annealing schedule as the main focus of the identical consideration to element: The authors use Adam with (beta_1=0.9), a non-default (beta_2=0.98), (epsilon = 10^{-9}), and arguably one of the elaborate annealing schedules for the educational charge (eta):
(eta = d_text{mannequin}^{-0.5} cdot min(steptext{_}num^{-0.5}, steptext{_}num cdot warmuptext{_}steps^{-1.5}) )
the place (d_text{mannequin}) is the variety of parameters of the mannequin and (warmuptext{_}steps = 4000).
One other latest paper by Smith et al. (2017) demonstrates an attention-grabbing connection between the educational charge and the batch dimension, two hyperparameters which can be usually considered impartial of one another: They present that decaying the educational charge is equal to rising the batch dimension, whereas the latter permits for elevated parallelism. Conversely, we will cut back the variety of mannequin updates and thus velocity up coaching by rising the educational charge and scaling the batch dimension. This has ramifications for large-scale Deep Studying, which may now repurpose present coaching schedules with no hyperparameter tuning.
Heat restarts
SGD with restarts
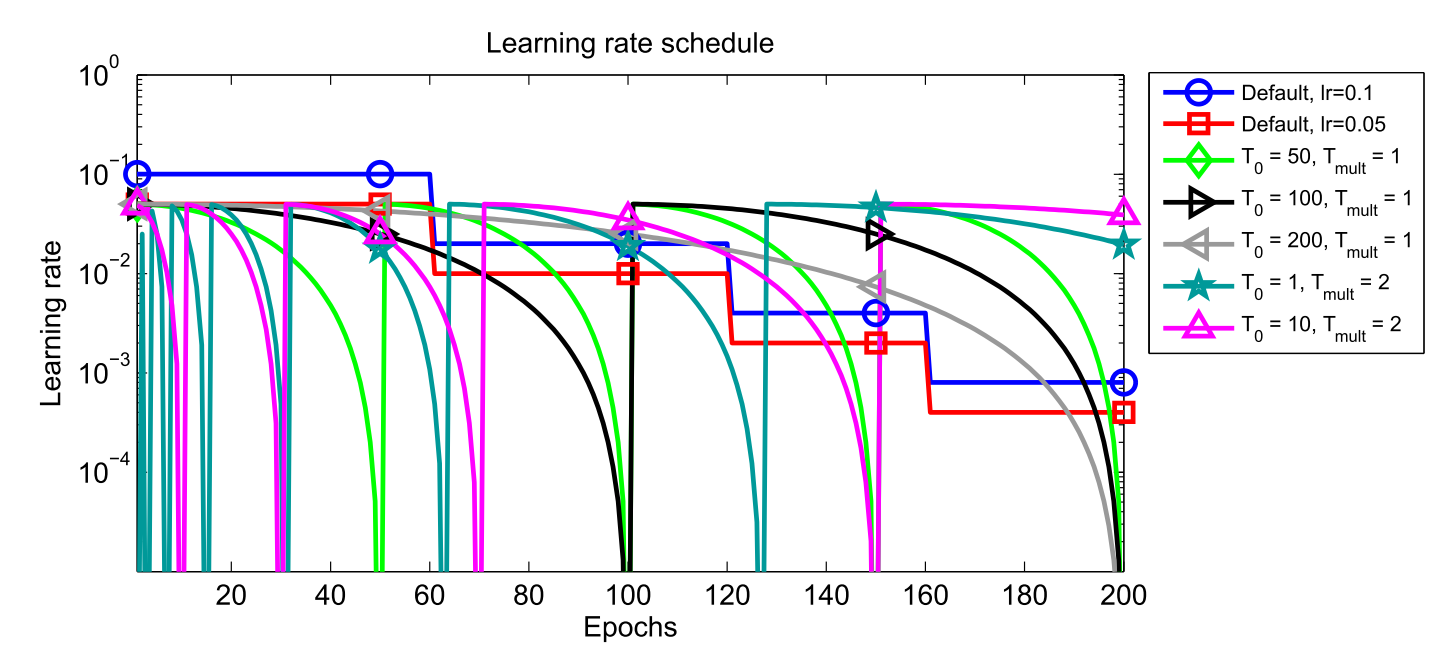
One other efficient latest growth is SGDR (Loshchilov and Hutter, 2017) , an SGD different that makes use of heat restarts as an alternative of studying charge annealing. In every restart, the educational charge is initialized to some worth and is scheduled to lower. Importantly, the restart is heat because the optimization doesn’t begin from scratch however from the parameters to which the mannequin converged over the past step. The important thing issue is that the educational charge is decreased with an aggressive cosine annealing schedule, which quickly lowers the educational charge and appears like the next:
(eta_t = eta_{min}^i + dfrac{1}{2}(eta_{max}^i – eta_{min}^i)(1 + textual content{cos}(dfrac{T_{cur}}{T_i}pi)) )
the place (eta_{min}^i) and (eta_{max}^i) are ranges for the educational charge through the (i)-th run, (T_{cur}) signifies what number of epochs handed because the final restart, and (T_i) specifies the epoch of the following restart. The nice and cozy restart schedules for (T_i=50), (T_i=100), and (T_i=200) in contrast with common studying charge annealing are proven in Determine 1.
2017)
The excessive preliminary studying charge after a restart is used to primarily catapult the parameters out of the minimal to which they beforehand converged and to a distinct space of the loss floor. The aggressive annealing then permits the mannequin to quickly converge to a brand new and higher resolution. The authors empirically discover that SGD with heat restarts requires 2 to 4 instances fewer epochs than studying charge annealing and achieves comparable or higher efficiency.
Studying charge annealing with heat restarts is also referred to as cyclical studying charges and has been initially proposed by Smith (2017) . Two extra articles by college students of quick.ai (which has not too long ago began to show this methodology) that debate heat restarts and cyclical studying charges may be discovered right here and right here.
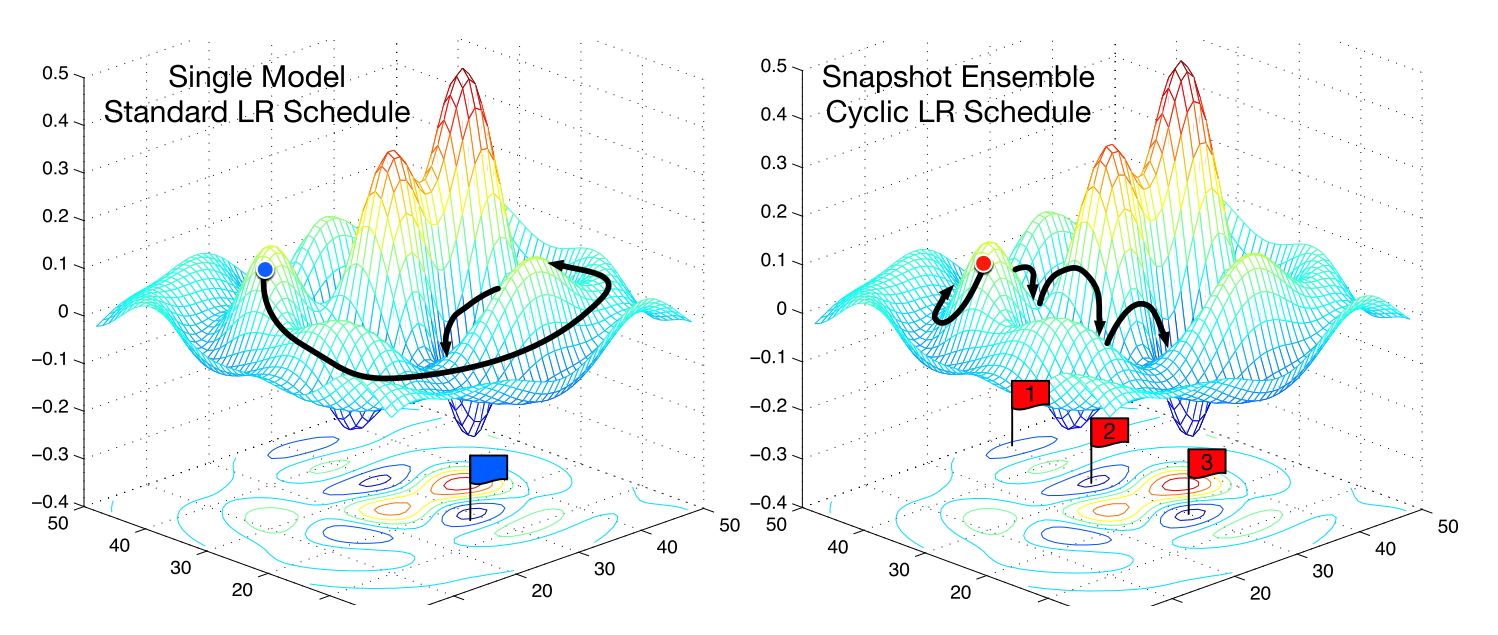
Snapshot ensembles
Snapshot ensembles (Huang et al., 2017) are a intelligent, latest approach that makes use of heat restarts to assemble an ensemble primarily without spending a dime when coaching a single mannequin. The strategy trains a single mannequin till convergence with the cosine annealing schedule that we’ve got seen above. It then saves the mannequin parameters, performs a heat restart, after which repeats these steps (M) instances. In the long run, all saved mannequin snapshots are ensembled. The frequent SGD optimization behaviour on an error floor in comparison with the behaviour of snapshot ensembling may be seen in Determine 2.
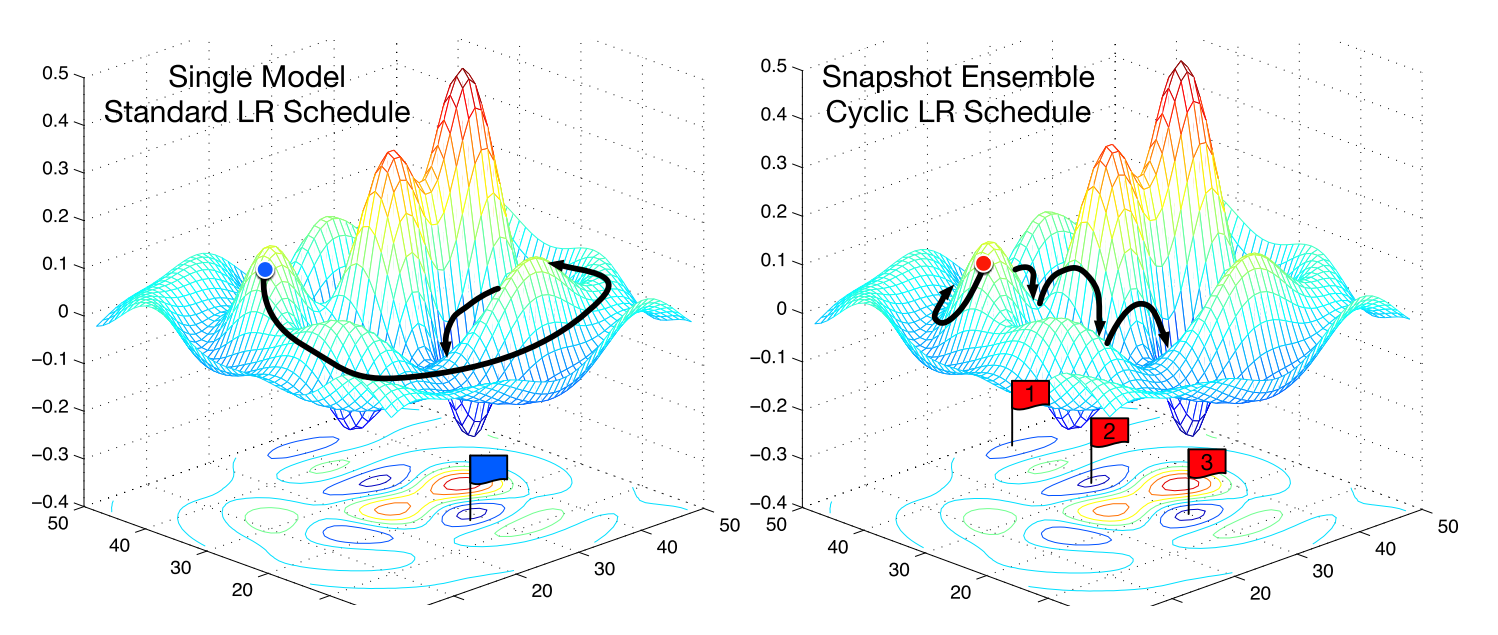
The success of ensembling basically depends on the variety of the person fashions within the ensemble. Snapshot ensembling thus depends on the cosine annealing schedule’s means to allow the mannequin to converge to a distinct native optimum after each restart. The authors display that this holds in follow, attaining state-of-the-art outcomes on CIFAR-10, CIFAR-100, and SVHN.
Adam with restarts
Heat restarts didn’t work initially with Adam resulting from its dysfunctional weight decay, which we’ve got seen earlier than. After fixing weight decay, Loshchilov and Hutter (2017) equally prolong Adam to work with heat restarts. They set (eta_{min}^i=0) and (eta_{max}^i=1), which yields:
(eta_t = 0.5 + 0.5 : textual content{cos}(dfrac{T_{cur}}{T_i}pi)))
They suggest to start out with an initially small (T_i) (between (1%) and (10%) of the whole variety of epochs) and multiply it by an element of (T_{mult}) (e.g. (T_{mult}=2)) at each restart.
Studying to optimize
One of the vital attention-grabbing papers of final 12 months (and reddit’s “Finest paper identify of 2016” winner) was a paper by Andrychowicz et al. (2016) the place they prepare an LSTM optimizer to supply the updates to the principle mannequin throughout coaching. Sadly, studying a separate LSTM optimizer and even utilizing a pre-trained LSTM optimizer for optimization drastically will increase the complexity of mannequin coaching.
One other very influential learning-to-learn paper from this 12 months makes use of an LSTM to generate mannequin architectures in a domain-specific language (Zoph and Quoc, 2017) . Whereas the search course of requires huge quantities of sources, the found architectures can be utilized as-is to interchange their present counterparts. This search course of has proved efficient and located architectures that obtain state-of-the-art outcomes on language modeling and outcomes aggressive with the state-of-the-art on CIFAR-10.
The identical search precept may be utilized to every other area the place key processes have been beforehand outlined by hand. One such area are optimization algorithms for Deep Studying. As we’ve got seen earlier than, optimization algorithms are extra related than they appear: All of them use a mix of an exponential shifting common of previous gradients (as in momentum) and of an exponential shifting common of previous squared gradients (as in Adadelta, RMSprop, and Adam) (Ruder, 2016) .
Bello et al. (2017) outline a domain-specific language that consists of primitives helpful for optimization akin to these exponential shifting averages. They then pattern an replace rule from the area of attainable replace guidelines, use this replace rule to coach a mannequin, and replace the RNN controller primarily based on the efficiency of the skilled mannequin on the take a look at set. The total process may be seen in Determine 3.
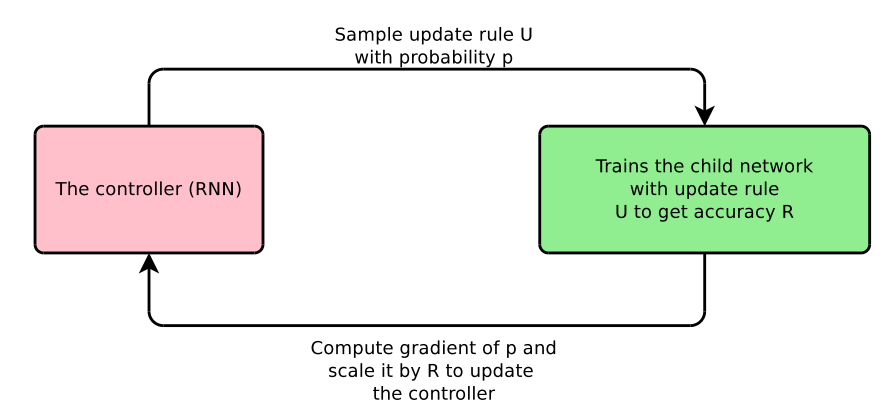
Specifically, they uncover two replace equations, PowerSign and AddSign. The replace equation for PowerSign is the next:
( theta_{t+1} = theta_{t} – alpha^{f(t)*
textual content{signal}(g_t)*textual content{signal}(m_t)}*g_t )
the place (alpha) is a hyperparameter that’s typically set to (e) or (2), (f(t)) is both (1) or a decay operate that performs linear, cyclical or decay with restarts primarily based on time step (t), and (m_t) is the shifting common of previous gradients. The frequent configuration makes use of (alpha=e) and no decay. We are able to observe that the replace scales the gradient by (alpha^{f(t)}) or (1/alpha^{f(t)}) relying on whether or not the path of the gradient and its shifting common agree. This means that this momentum-like settlement between previous gradients and the present one is a key piece of data for optimizing Deep Studying fashions.
AddSign in flip is outlined as follows:
( theta_{t+1} = theta_{t} – alpha + f(t) * textual content{signal}(g_t) * textual content{signal}(m_t)) * g_t)
with (alpha) typically set to (1) or (2). Much like the above, this time the replace scales (alpha + f(t)) or (alpha – f(t)) once more relying on the settlement of the path of the gradients. The authors present that PowerSign and AddSign outperform Adam, RMSprop, and SGD with momentum on CIFAR-10 and switch nicely to different duties akin to ImageNet classification and machine translation.
Understanding generalization
Optimization is intently tied to generalization because the minimal to which a mannequin converges defines how nicely the mannequin generalizes. Advances in optimization are thus intently correlated with theoretical advances in understanding the generalization behaviour of such minima and extra usually of gaining a deeper understanding of generalization in Deep Studying.
Nevertheless, our understanding of the generalization behaviour of deep neural networks remains to be very shallow. Current work confirmed that the variety of attainable native minima grows exponentially with the variety of parameters (Kawaguchi, 2016) . Given the large variety of parameters of present Deep Studying architectures, it nonetheless appears virtually magical that such fashions converge to options that generalize nicely, specifically on condition that they’ll fully memorize random inputs (Zhang et al., 2017) .
Keskar et al. (2017) establish the sharpness of a minimal as a supply for poor generalization: Specifically, they present that sharp minima discovered by batch gradient descent have excessive generalization error. This makes intuitive sense, as we usually would really like our features to be clean and a pointy minima signifies a excessive irregularity within the corresponding error floor. Nevertheless, newer work means that sharpness might not be such an excellent indicator in spite of everything by displaying that native minima that generalize nicely may be made arbitrarily sharp (Dinh et al., 2017) . A Quora reply by Eric Jang additionally discusses these articles.
An ICLR 2018 submission demonstrates by way of a sequence of ablation analyses {that a} mannequin’s reliance on single instructions in activation area, i.e. the activation of single items or characteristic maps is an efficient predictor of its generalization efficiency. They present that this holds throughout fashions skilled on totally different datasets and for various levels of label corruption. They discover that dropout doesn’t assist to resolve this, whereas batch normalization discourages single path reliance.
Whereas these findings point out that there’s nonetheless a lot we have no idea by way of Optimization for Deep Studying, you will need to keep in mind that convergence ensures and a big physique of labor exists for convex optimization and that present concepts and insights will also be utilized to non-convex optimization to some extent. The big-scale optimization tutorial at NIPS 2016 offers a superb overview of extra theoretical work on this space (see the slides half 1, half 2, and the video).
Conclusion
I hope that I used to be in a position to present an impression of a number of the compelling developments in optimization for Deep Studying over the previous 12 months. I’ve undoubtedly failed to say many different approaches which can be equally necessary and noteworthy. Please let me know within the feedback under what I missed, the place I made a mistake or misrepresented a way, or which side of optimization for Deep Studying you discover significantly thrilling or underexplored.
Hacker Information
You will discover the dialogue of this publish on HN right here.