A short information on multicollinearity and the way it impacts a number of regression fashions.

You’ll have obscure recollections out of your college statistics programs that multicollinearity is an issue for a number of regression fashions. However simply how problematic is multicollinearity? Properly, like many matters in statistics, the reply isn’t completely simple and will depend on what you’re eager to do together with your mannequin.
On this put up, I’ll step by a number of the challenges that multicollinearity presents in a number of regression fashions, and supply some instinct for why it may be problematic.
Collinearity and Multicollinearity
Earlier than shifting on, it’s a good suggestion to first nail down what collinearity and multicollinearity are. Fortunately, in case you’re accustomed to regression the ideas are fairly simple.
Collinearity exists if there’s a linear affiliation between two explanatory variables. What this suggests is, for all observations i, the next holds true:
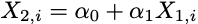
Multicollinearity is an extension of this concept and exists if there are linear associations between greater than two explanatory variables. For instance, you might need a state of affairs the place one variable is linearly related to two different variables in your design matrix, like so:
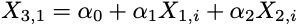
Strictly talking, multicollinearity is not correlation: fairly, it implies the presence of linear dependencies between a number of explanatory variables. This can be a nuanced level — however an vital one — and what each examples illustrate is a deterministic affiliation between predictors. This implies there are easy transforms that may be utilized to 1 variable to compute the precise worth for an additional. If that is doable, then we are saying we have now good collinearity or good multicollinearity.
When becoming a number of regression fashions, it’s precisely this that we have to keep away from. Particularly, a vital assumption for a number of regression is that there isn’t any good multicollinearity. So, we now know what good multicollinearity is, however why is it a downside?
Breaking Ranks
In a nutshell, the issue is redundancy as a result of completely multicollinear variables present the identical info.
For instance, take into account the dummy variable lure. Suppose we’re supplied with a design matrix that features two dummy coded {0, 1} columns. Within the first column rows corresponding with “sure” responses are given a worth of 1. Within the second column, nevertheless, rows which have “no” responses are assigned a worth of 1. On this instance, the “no” column is totally redundant as a result of it may be computed from the “sure” column ( “No” = 1 — “Sure”). Due to this fact, we don’t require a separate column to encode “no” responses as a result of the zeroes within the “sure” column present the identical info.
Let’s lengthen this concept of redundancy a bit additional by contemplating the matrix beneath:
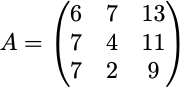
Right here, the primary two columns are linearly impartial; nevertheless, the third is definitely a linear mixture of columns one and two (the third column is the sum of the primary two). What this implies is, if columns one and three, or columns two and three, are recognized, the remaining column can all the time be computed. The upshot right here is that, at most, there can solely be two columns that make genuinely impartial contributions — the third will all the time be redundant.
The downstream impact of redundancy is that it makes the estimation of mannequin parameters unattainable. Earlier than explaining why it’ll be helpful to shortly outline the moments matrix:
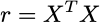
Critically, to derive the odd least squares (OLS) estimators r have to be invertible, which implies the matrix will need to have full rank. If the matrix is rank poor then the OLS estimator doesn’t exist as a result of the matrix can’t be inverted.
Okay, so what does this all imply?
With out going into an excessive amount of element, the rank of a matrix is the dimension of the vector house spanned by its columns. The best solution to parse this definition is as follows: in case your design matrix incorporates okay impartial explanatory variables, then rank(r) ought to equal okay. The impact of good multicollinearity is to scale back the rank of r to some worth lower than the utmost variety of columns within the design matrix. The matrix A above, then, solely has a rank of two and is rank poor.
Intuitively, in case you’re throwing okay items of data into the mannequin, you ideally need every to make a helpful contribution. Every variable ought to carry its personal weight. Should you as a substitute have a variable that’s utterly depending on one other then it received’t be contributing something helpful, which can trigger r to grow to be degenerate.
Imperfect Associations
Up till this level, we have now been discussing the worst-case situation the place variables are completely multicollinear. In the actual world, nevertheless, it’s fairly uncommon that you simply’ll encounter this downside. Extra realistically you’ll encounter conditions the place there are approximate linear associations between two or extra variables. On this case, the linear affiliation will not be deterministic, however as a substitute stochastic. This may be described by rewriting the equation above and introducing an error time period:
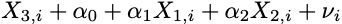
This case is extra manageable and doesn’t essentially consequence within the degeneracy of r. However, if the error time period is small, the associations between variables could also be almost completely multicollinear. On this case, although it’s true that rank(r) = okay, mannequin becoming could grow to be computationally unstable and produce coefficients that behave fairly erratically. For instance, pretty small adjustments in your knowledge can have large results on coefficient estimates, thereby lowering their statistical reliability.
Inflated Fashions
Okay, so stochastic multicollinearity presents some hurdles in case you’re eager to make statistical inferences about your explanatory variables. Particularly, what it does is inflate the usual errors round your estimated coefficients which may end up in a failure to reject the null speculation when a real impact is current (Sort II error). Fortuitously, statisticians have come to the rescue and have created some very helpful instruments to assist diagnose multicollinearity.
One such software is the variance inflation issue (VIF) which quantifies the severity of multicollinearity in a a number of regression mannequin. Functionally, it measures the rise within the variance of an estimated coefficient when collinearity is current. So, for covariate j, the VIF is outlined as follows:
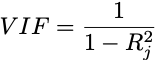
Right here, the coefficient of dedication is derived from the regression of covariate j in opposition to the remaining okay — 1 variables.
The interpretation of the VIF is pretty simple, too. If the VIF is shut to 1 this suggests that covariate j is linearly impartial of all different variables. Values higher than one are indicative of some extent of multicollinearity, whereas values between one and 5 are thought-about to exhibit gentle to reasonable multicollinearity. These variables could also be left within the mannequin, although some warning is required when deciphering their coefficients. I’ll get to this shortly. If the VIF is bigger than 5 this means reasonable to excessive multicollinearity, and also you may need to take into account leaving these variables out. If, nevertheless, the VIF > 10, you’d in all probability have an inexpensive foundation for dumping that variable.
A really good property of the VIF is that its sq. root indexes the rise within the coefficient’s normal error. For instance, if a variable has a VIF of 4, then its normal error shall be 2 occasions bigger than if it had zero correlation with all different predictors.
Okay, now the cautionary bit: in case you do determine to retain variables which have a VIF > 1 then the magnitudes of the estimated coefficients not present a wholly exact measure of affect. Recall that the regression coefficient for variable j displays the anticipated change within the response, per unit enhance in j alone, whereas holding all different variables fixed. This interpretation breaks down if an affiliation exists between explanatory variable j and a number of other others as a result of any change in j is not going to independently affect the response variable. The extent of this, after all, will depend on how excessive the VIF is however it’s actually one thing to remember of.
Design Points
Thus far we have now explored two fairly problematic aspects of multicollinearity:
1) Good multicollinearity: defines a deterministic relationship between covariates and produces a degenerate moments matrix, thereby making estimation by way of OLS unattainable; and
2) Stochastic multicollinearity: covariates are roughly linearly dependent however the rank of the moments matrix will not be affected. It does create some complications in deciphering mannequin coefficients and statistical inferences about them, notably when the error time period is small.
You’ll discover, although, that these points solely concern calculations about predictors — nothing has been mentioned concerning the mannequin itself. That’s as a result of multicollinearity solely impacts the design matrix and never the general match of the mannequin.
So…..downside, or not? Properly, as I mentioned at first, it relies upon.
If all you’re concerned about is how effectively your assortment of explanatory variables predicts the response variable, then the mannequin will nonetheless yield legitimate outcomes, even when multicollinearity is current. Nonetheless, if you wish to make particular claims about particular person predictors then multicollinearity is extra of an issue; however in case you’re conscious of it you may take actions to mitigate its affect, and in a later put up I’ll define what these actions are.
Within the meantime, I hope you discovered one thing helpful on this put up. In case you have any questions, ideas, or suggestions, be happy to depart me a remark.
Should you loved this put up and want to keep updated then please take into account following me on Medium. It will make sure you don’t miss out on new content material. You can too comply with me on LinkedIn and Twitter if that’s extra your factor
Multicollinearity: Drawback, or Not? was initially revealed in In the direction of Information Science on Medium, the place persons are persevering with the dialog by highlighting and responding to this story.


