This put up provides a quick overview of modularity in deep studying. For a extra in-depth evaluation, seek advice from our survey. For modular fine-tuning for NLP, try our EMNLP 2022 tutorial. For extra sources, try modulardeeplearning.com.
Fuelled by scaling legal guidelines, state-of-the-art fashions in machine studying have been rising bigger and bigger. These fashions are monoliths. They’re pre-trained from scratch in extremely choreographed engineering endeavours. On account of their dimension, fine-tuning has turn out to be costly whereas alternate options, akin to in-context studying are sometimes brittle in observe. On the identical time, these fashions are nonetheless unhealthy at many issues—symbolic reasoning, temporal understanding, producing multilingual textual content, and many others.
Modularity could assist us handle a few of these excellent challenges. By modularising fashions, we will separate elementary information and reasoning skills about language, imaginative and prescient, and many others from area and task-specific capabilities. Modularity additionally supplies a flexible option to lengthen fashions to new settings and to enhance them with new skills.
We give an in-depth overview of modularity in our survey on Modular Deep Studying. Within the following, I’ll spotlight a number of the most essential observations and takeaways associated to the next ideas:
- Taxonomy
- Computation Perform
- Routing Perform
- Aggregation Perform
- Coaching Setting
- Functions of Modularity
- Purposes in Switch Studying
- Future Instructions
- Conclusion
Taxonomy
We categorise modular approaches primarily based on 4 dimensions:
- Computation operate: How the module is carried out.
- Routing operate: How lively modules are chosen.
- Aggregation operate: How outputs of lively modules are aggregated.
- Coaching setting: How modules are educated.
We offer case research of various configurations of those elements under.
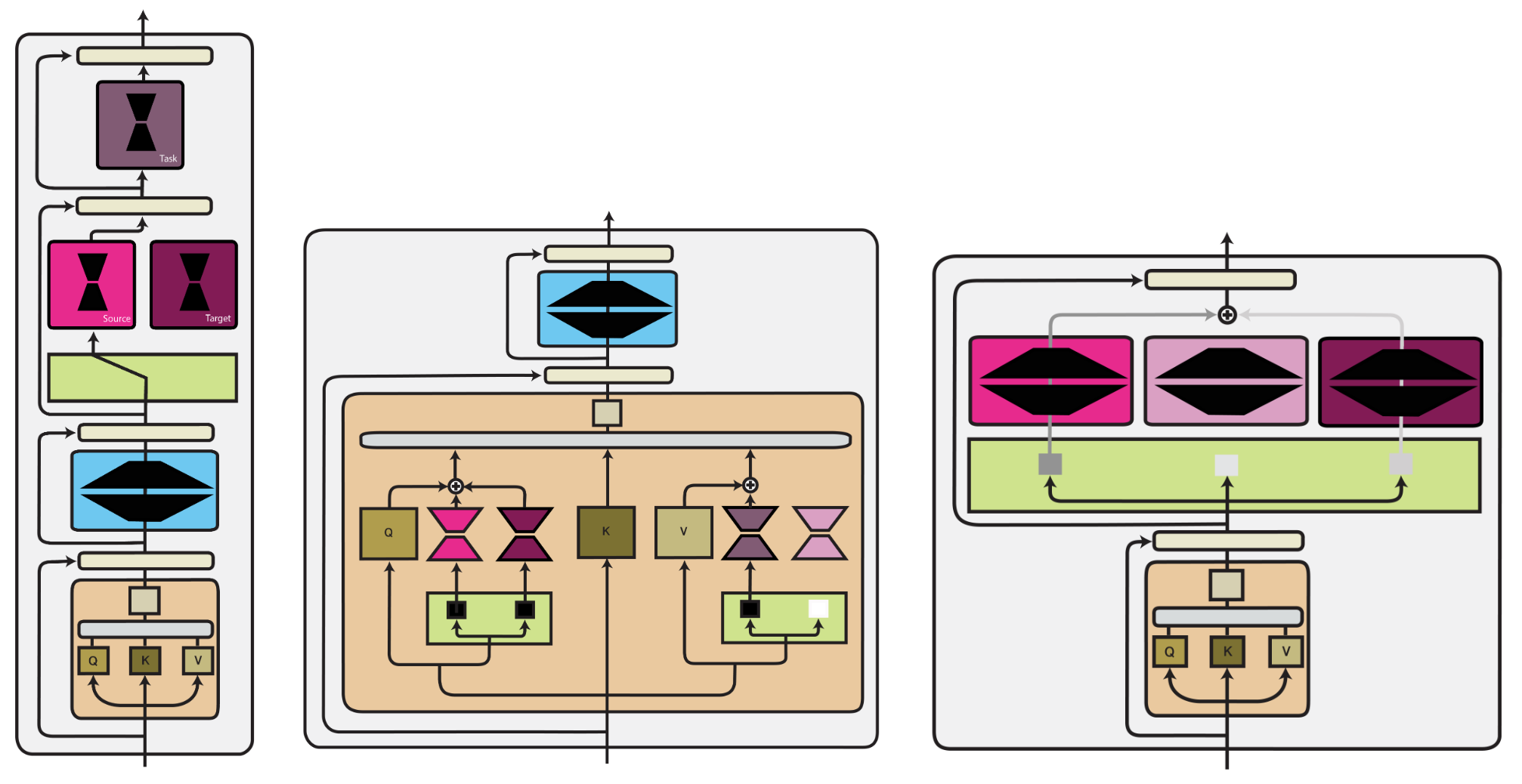
Computation Perform
We take into account a neural community $f_theta$ as a composition of features $f_{theta_1} odot f_{theta_2} odot ldots odot f_{theta_l}$, every with their very own set of parameters $theta_i$. A operate could be a layer or a part of a layer akin to a linear transformation.
We establish three core varieties of computation features that compose a module with parameters $phi$ with a mannequin’s features:
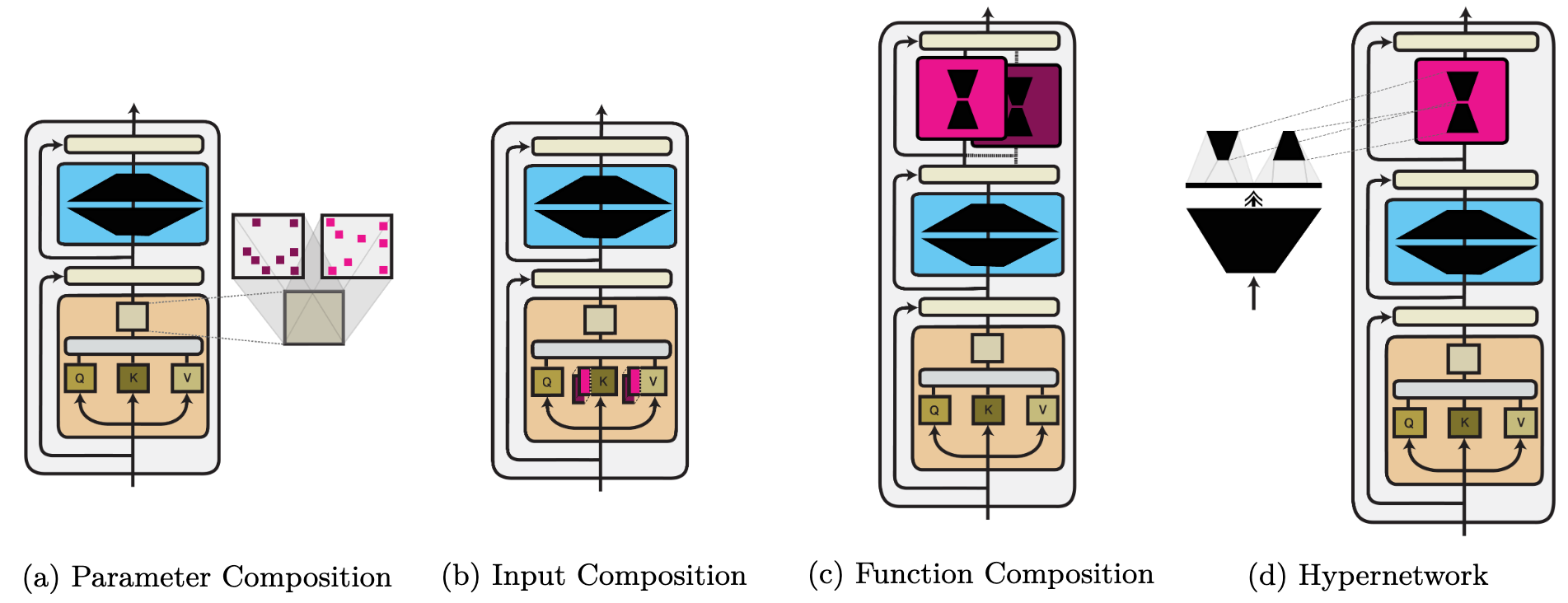
- Parameter composition. Modules modify the mannequin on the extent of particular person weights: $f_i^prime(boldsymbol{x}) = f_{theta_i oplus phi}(boldsymbol{x})$.
- Enter composition. A operate’s enter $boldsymbol{x}$ is concatenated with the module parameters: $f_i^prime(boldsymbol{x}) = f_{theta_i}([boldsymbol{x}, phi])$.
- Perform composition. The outputs of the mannequin’s operate and the module are mixed: $f_i^prime(boldsymbol{x}) = f_{theta_i} odot f_{phi}(boldsymbol{x})$.
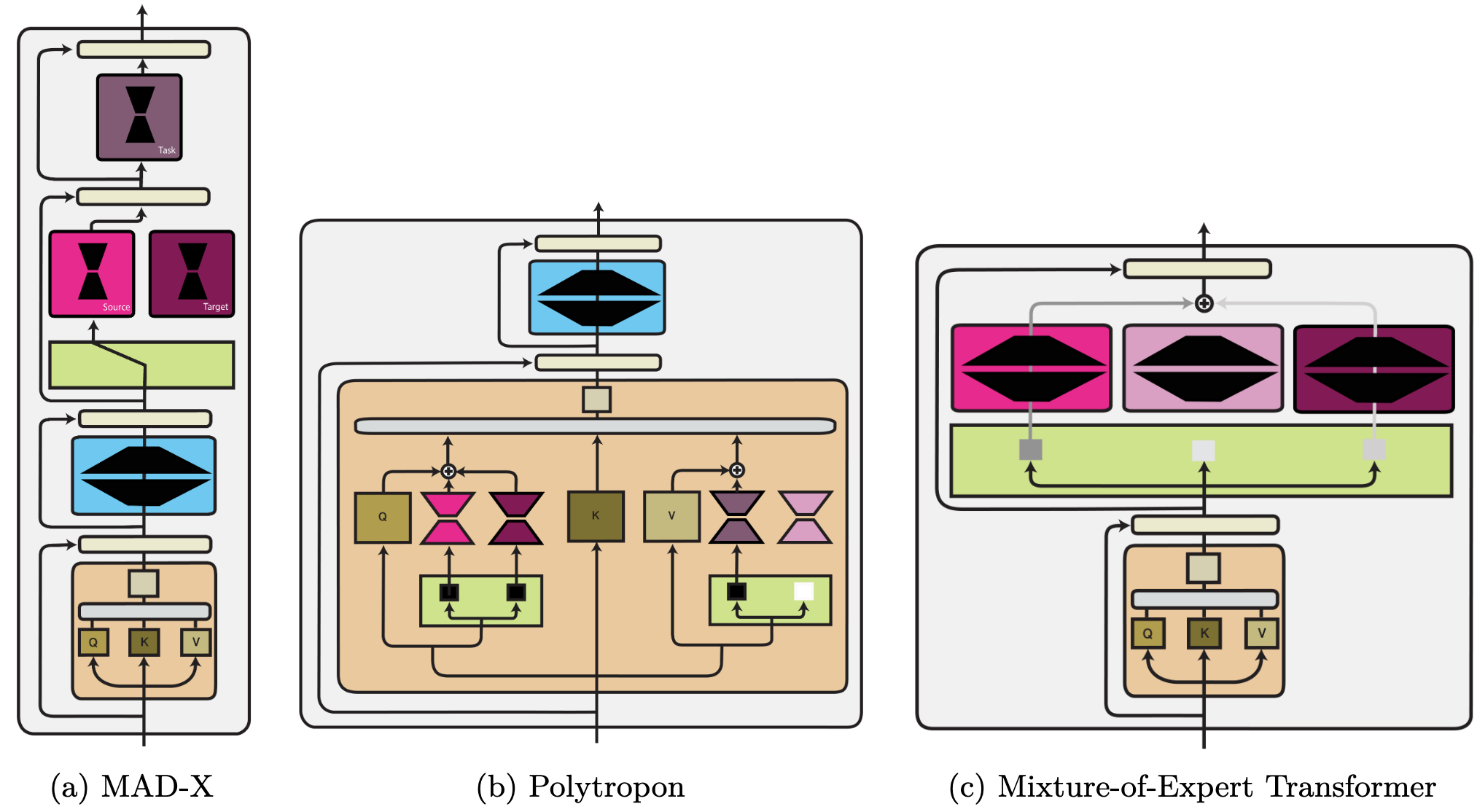
We offer an summary of the three comptuation features (along with a hypernetwork) as a part of a Transformer structure under:
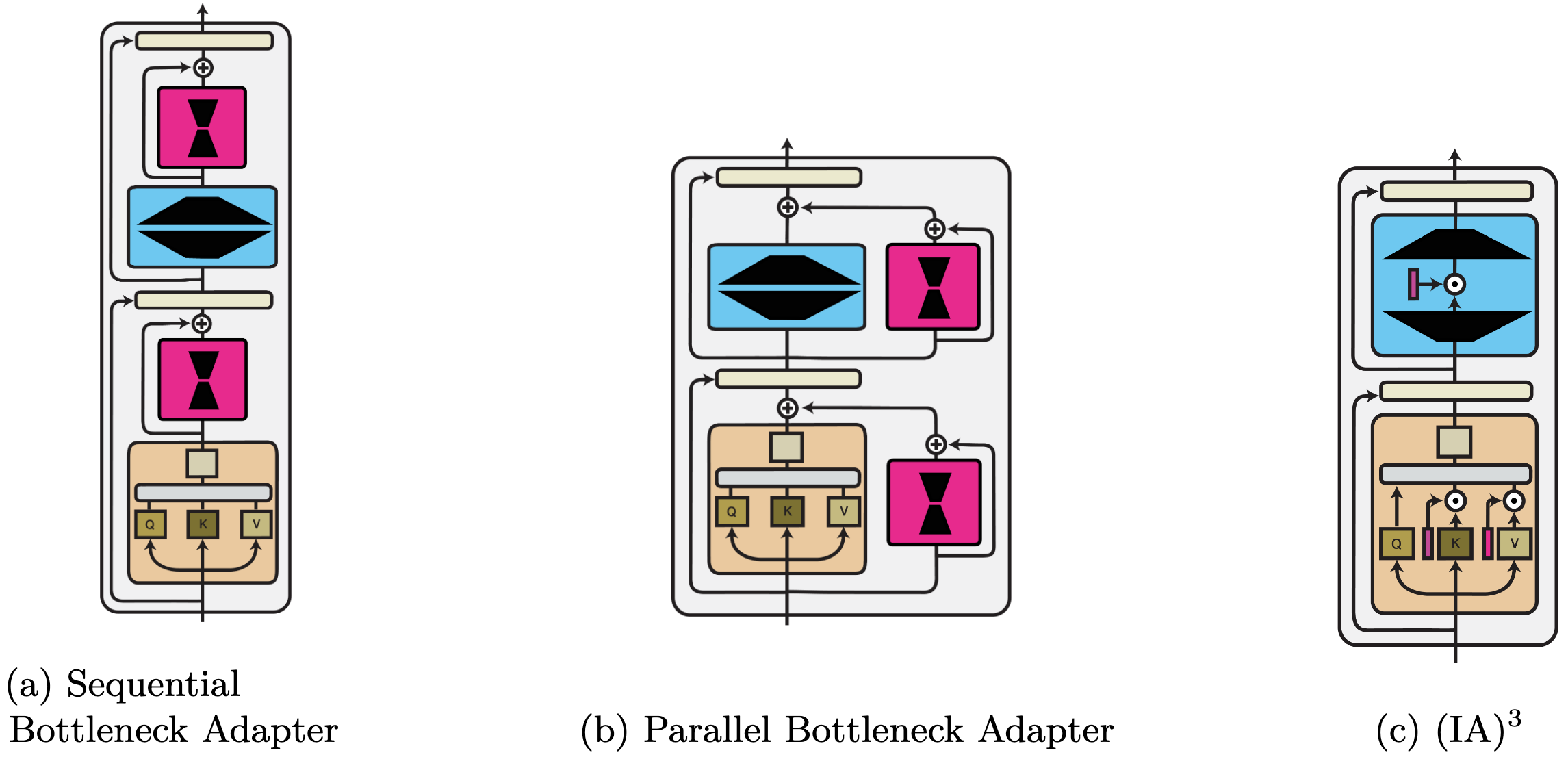
Parameter composition. We establish two fundamental methods modules are used to alter the parameters of a mannequin: a) updating a sparse subset of parameters and b) updating parameters in a low-dimensional subspace. Sparse strategies are intently associated to pruning and the lottery ticket speculation. Sparse strategies could be structured and solely utilized to particular parameter teams.
Enter composition. Immediate-based studying could be seen as discovering a task-specific textual content immediate whose embedding $phi$ elicits the specified behaviour. Alternatively, steady prompts could be discovered instantly—within the enter or at every layer of a mannequin.
Perform composition. That is essentially the most basic class. It subsumes customary multi-task studying strategies, modules that adapt a pre-trained mannequin (often called ‘adapters’), and rescaling strategies. As well as, parameter and enter composition strategies will also be expressed as operate composition. For illustration, we offer examples of three operate composition strategies under.
Module parameter era. As a substitute of studying module parameters instantly, they are often generated utilizing an auxiliary mannequin (a hypernetwork) conditioned on further info and metadata.
We offer a high-level overview of a number of the trade-offs of the completely different computation features under. Discuss with the tutorial slides or the survey for detailed explanations.
| Parameter effectivity | Coaching effectivity | Inference effectivity | Efficiency | Compositionality | |
|---|---|---|---|---|---|
| Parameter composition | + | – | ++ | + | + |
| Enter composition | ++ | — | — | – | + |
| Perform composition | – | + | – | ++ | + |
Routing Perform
A routing operate $r(cdot)$ determines which modules are lively primarily based on a given enter by assigning a rating $alpha_i$ to every module from a listing $M$. We give an summary of the completely different routing strategies under.
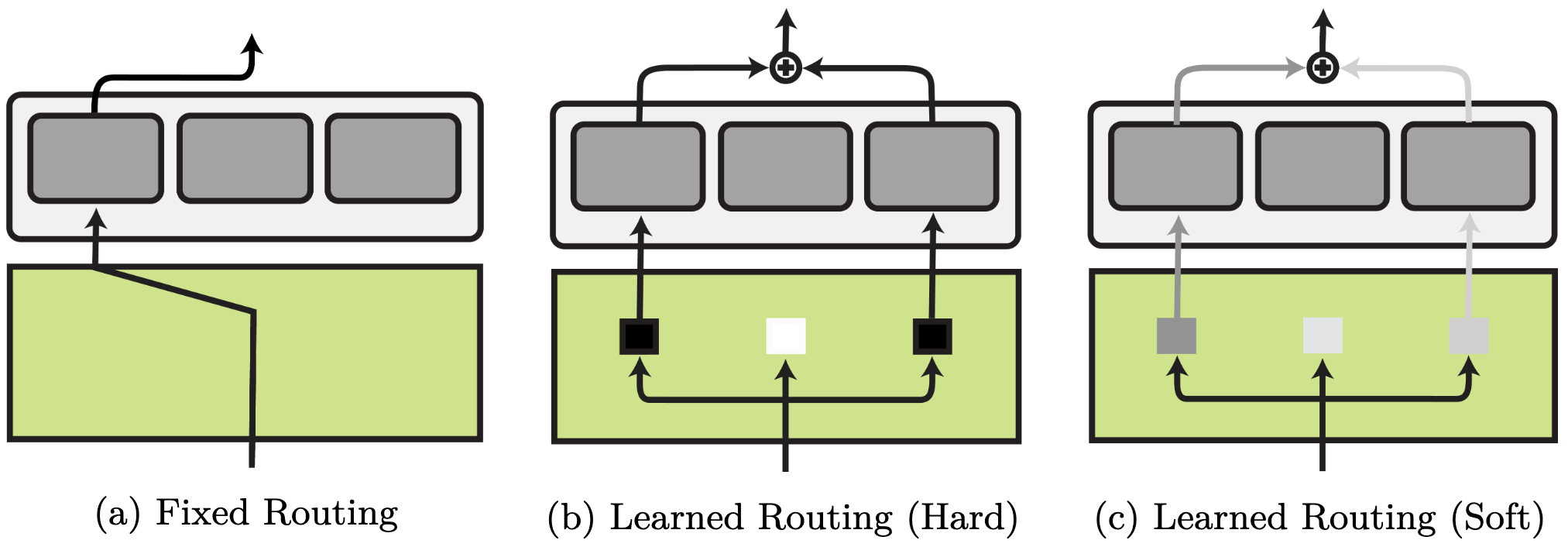
The routing operate could be mounted and every routing choice is made primarily based on prior information in regards to the process. Alternatively, routing could be discovered. Realized routing strategies differ in whether or not they be taught a arduous, binary number of modules or a smooth choice by way of a likelihood distribution over modules.
Mounted routing. Mounted routing employs metadata akin to the duty identification to make discrete routing selections earlier than coaching. Mounted routing is utilized in most operate composition strategies akin to multi-task studying and adapters. Mounted routing can choose completely different modules for various elements of the goal setting akin to process and language in NLP or robotic and process in RL, which permits generalisation to unseen situations.
Realized routing. Realized routing is often carried out by way of an MLP and introduces further challenges, together with coaching instability, module collapse, and overfitting. Present discovered routing strategies are sometimes sub-optimal as they under-utilise and under-specialise modules. Nonetheless, when there is no such thing as a one-to-one mapping between process and corresponding talent, they’re the one possibility obtainable.
Laborious discovered routing. Laborious discovered routing fashions the selection of whether or not a module is lively as a binary choice. As discrete selections can’t be discovered instantly with gradient descent, strategies be taught arduous routing by way of reinforcement studying, evolutionary algorithms, or stochastic re-parametrisation.
Tender discovered routing. Tender routing strategies sidestep a discrete number of modules by studying a weighted mixture within the type of a likelihood distribution over obtainable modules. A basic instance is combination of specialists. As activating all modules is pricey, latest strategies be taught to solely route the top-$okay$ and even top-1 modules. Routing on the token stage results in extra environment friendly coaching however limits the expressiveness of modular representations.
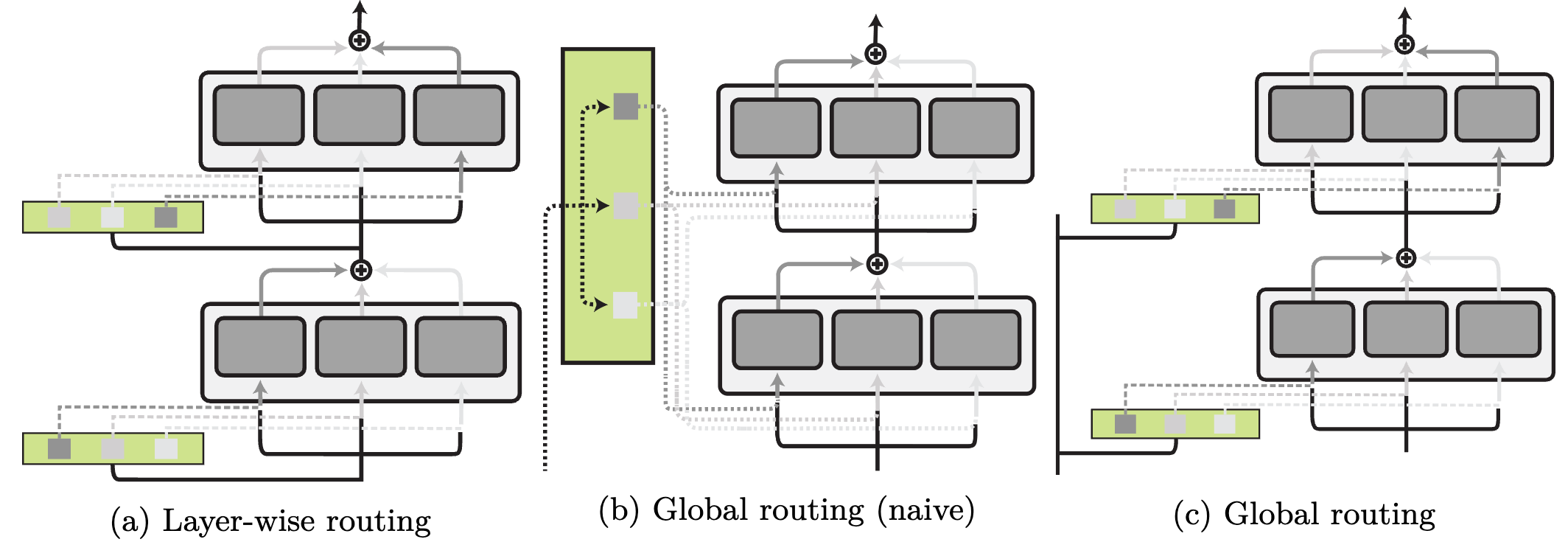
Degree of routing. Routing can choose modules globally for your entire community, make completely different allocations per layer, and even make hierarchical routing selections. We illustrate completely different routing ranges under.
Aggregation Perform
The aggregation operate determines how the outputs of modules chosen by way of routing are mixed. In observe, routing and aggregation are sometimes mixed. Aggregation features could be categorised equally to computation features; whereas computation features compose shared mannequin components with module elements, aggregation features mixture a number of module elements on completely different ranges:
- Parameter aggregation. Module parameters are aggregated: $f_i^prime(boldsymbol{x}) = f_{boldsymbol{phi_i}^{1} oplus dots oplus boldsymbol{phi}_i^M}(boldsymbol{x})$.
- Illustration aggregation. Modular representations are aggregated: $f_i^prime(boldsymbol{x}) = f_{boldsymbol{theta}_i}(boldsymbol{x}) oplus f_{boldsymbol{phi}_i^1}(boldsymbol{x}) oplus dots oplus f_{boldsymbol{phi}_i^M}(boldsymbol{x})$.
- Enter aggregation. Module parameters are concatenated on the enter stage: $f_i^prime(boldsymbol{x}) = f_{boldsymbol{theta_i}}([boldsymbol{phi_i^1}, dots, boldsymbol{phi_i^M}, boldsymbol{x}])$.
- Perform aggregation. Modular features are aggregated: $f_i^prime(boldsymbol{x}) = f_{boldsymbol{phi}_i^{1}} circ … circ f_{boldsymbol{phi}_i^M}(boldsymbol{x})$.
Parameter aggregation. Aggregating info from a number of modules by interpolating their weights is intently linked to linear mode connectivity, which reveals that below sure situations akin to the identical initialisation, two networks are linked by a linear path of non-increasing error. Primarily based on this assumption, modular edits could be carried out on a mannequin utilizing arithmetic operations as a way to take away or elicit sure info within the mannequin.
Illustration aggregation. Alternatively, the outputs of various modules could be interpolated by aggregating the modules’ hidden representations. One option to carry out this aggregation is to be taught a weighted sum of representations, just like how routing learns a rating $alpha_i$ per module. We will additionally be taught a weighting that takes into consideration the hidden representations, akin to by way of consideration.
Enter aggregation. In prompting, offering a mannequin with a number of directions or a number of exemplars by way of concatenation could be seen as a type of enter aggregation. Tender prompts could be discovered for various settings akin to process and language or attributes and objects and aggregated by way of concatenation.
Perform aggregation. Lastly, we will mixture modules on the operate stage by various the order of computation. We will mixture them sequentially the place the output of 1 module is the enter of the subsequent module, and many others. For extra complicated module configurations, we will mixture modules hierarchically primarily based on a tree construction.
Coaching Setting
The final dimension alongside which we will differentiate modular strategies is the way in which they’re educated. We establish three modular coaching methods: 1) joint coaching; 2) continuous studying, and three) post-hoc adaptation.
Joint coaching. In multi-task studying settings, modular task-specific elements are educated collectively to mitigate catastrophic interference, with mounted or discovered routing. Joint coaching may also present a helpful initialisation for modular parameters and permit for the extra of modular elements in later levels.
Continuous studying. Throughout continuous studying, new modules are launched into the mannequin over time. The parameters of earlier modules are usually frozen whereas new modules are linked to current modules in several methods.
Submit-hoc adaptation. These strategies are also referred to as parameter-efficient fine-tuning as they’re usually used to adapt a big pre-trained mannequin to a goal setting. We cowl such strategies for NLP in our EMNLP 2022 tutorial.
Functions of Modularity
Most of the above strategies are evaluated primarily based on their skill to scale giant fashions or allow few-shot switch. Modularity can be essential for different purposes involving planning and systematic generalisation, together with 1) hierarchical reinforcement studying; 2) neural programme induction; and three) neural causal inference. We illustrate them under.
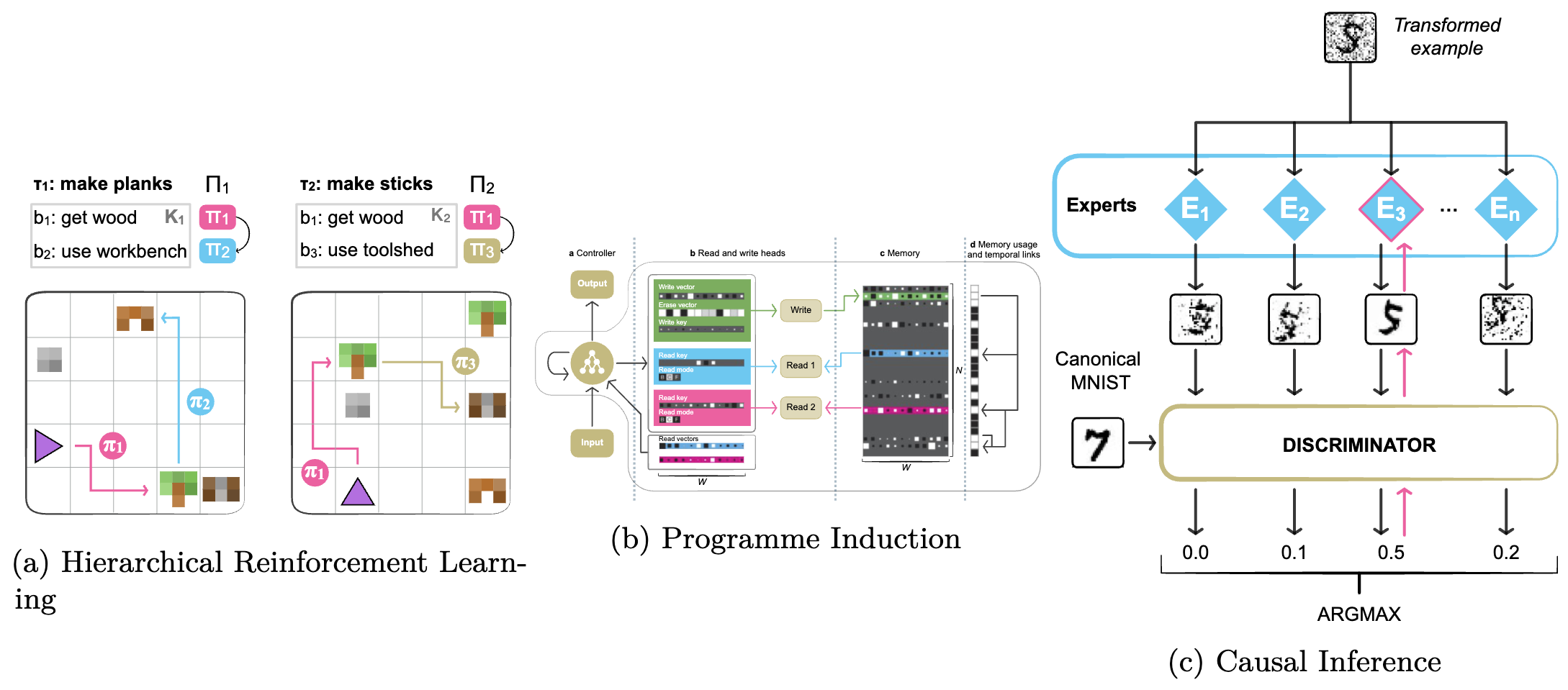
Hierarchical reinforcement studying. With the intention to be taught over giant time spans or with very sparse and delayed rewards in RL, it’s typically helpful to be taught intermediate abstractions, often called choices or expertise, within the type of transferable sub-policies. Studying sub-policies introduces challenges associated to specialisation and supervision and the area of actions and choices. Methods used to deal with them contain intrinsic rewards, sub-goals, and language as an intermediate area.
Programme simulation. Modularity will also be used to simulate programmes by establishing a programme graph dynamically primarily based on an enter or globally primarily based on a process description. Along with routing and computation features, such architectures could be prolonged with an exterior reminiscence. Programme simulation is beneficial when duties depend on performing the right sequence of sub-tasks.
Causal inference. Modularity in causal inference strategies displays the modularity within the (bodily) mechanisms of the world. As modules are assumed to be impartial and reusable, ML fashions mirroring this construction are extra sturdy to interventions and native distribution shifts. Challenges embrace specialising every module in direction of a selected mechanism in addition to collectively studying summary representations and their interplay in a causal graph.
Purposes in Switch Studying
The offered strategies are utilized in a wide range of purposes. We first spotlight widespread purposes in NLP after which draw analogies to purposes in speech, pc imaginative and prescient, and different areas of machine studying.
Machine translation. In MT, bilingual adapters have been used to adapt a massively multilingual NMT mannequin to a selected supply–goal translation route. Such work has been prolonged to extra environment friendly monolingual adapters. Hypernetworks have been used to allow constructive switch between languages. Different approaches akin to language and domain-specific subnetworks and mixture-of-experts have additionally been utilized.
Cross-lingual switch. Language modules are mixed with process modules to allow switch of huge fashions fine-tuned on a process in a supply language to a unique goal language. Inside this framework, many variations have been proposed that be taught adapters for language pairs or language households, be taught language and process subnetworks, or use a hypernetwork for the era of assorted elements.
Area adaptation. Area-specific modular representations have been discovered utilizing adapters or subnetworks. A typical design is to make use of a set of shared modules and area modules which can be discovered collectively, with further regularisation or loss phrases on the module parameters.
Information injection. Modules will also be used to retailer and inject exterior information, which could be mixed with language, area, or process information. A typical technique is to coach modules on artificial information created primarily based on the data in a information base.
Speech processing. In speech, related strategies have been explored as in NLP. The primary variations are that the underlying mannequin is often a wav2vec variant and modular representations are optimised primarily based on the CTC goal. The most typical setting is to be taught adapters for ASR.
Pc imaginative and prescient and cross-modal studying. In pc imaginative and prescient, widespread module selections are adapters and subnetworks primarily based on ResNet or Imaginative and prescient Transformer fashions. For multi-modal studying, process and modality info are captured in separate modules for various purposes. The latest Flamingo mannequin, as an illustration, makes use of frozen pretrained imaginative and prescient and language fashions and learns new adapter layers to situation the language representations on visible inputs.
Future Instructions
Future instructions embrace combining completely different computation features, gaining a greater understanding of the character and variations of various modular representations, integrating discovered routing in pre-training, benchmarking routing strategies, composing subnetwork info instantly, creating discovered aggregation strategies, and creating extensible modular multi-task fashions, amongst others.
Conclusion
We now have offered a categorisation of modularity in deep studying throughout 4 core dimensions. Given the development of pre-training bigger and bigger fashions, we imagine modularity can be essential. It’ll allow extra sustainable mannequin improvement by modularising components and creating modular strategies that handle present limitations and could be shared throughout completely different architectures. However modularity may facilitate a shift away from a focus of mannequin improvement in a number of establishments and to distributing the event of modular elements throughout the group.
Quotation
For attribution in educational contexts or books, please cite our survey as:
Jonas Pfeiffer and Sebastian Ruder and Ivan Vulić and Edoardo M. Ponti, "Modular Deep Studying". arXiv preprint arXiv:2302.11529, 2023.
BibTeX quotation
@article{pfeiffer2023modulardeeplearning,
creator = {Pfeiffer, Jonas and Ruder, Sebastian and Vuli{'c}, Ivan and Ponti, Edoardo M.},
title = {{Modular Deep Studying}},
yr = {2023},
journal = {CoRR},
quantity = {abs/2302.11529},
url = {https://arxiv.org/abs/2302.11529},
}Please cite our tutorial as:
Sebastian Ruder and Jonas Pfeiffer and Ivan Vulić. "Modular and Parameter-Environment friendly High quality-Tuning for {NLP} Fashions". Proceedings of the 2022 Convention on Empirical Strategies in Pure Language Processing: Tutorial Abstracts, 2022.
BibTeX quotation:
@inproceedings{ruder-etal-2022-modular,
title = "Modular and Parameter-Environment friendly High quality-Tuning for {NLP} Fashions",
creator = "Ruder, Sebastian and
Pfeiffer, Jonas and
Vuli{'c}, Ivan",
booktitle = "Proceedings of the 2022 Convention on Empirical Strategies in Pure Language Processing: Tutorial Abstracts",
month = dec,
yr = "2022",
handle = "Abu Dubai, UAE",
writer = "Affiliation for Computational Linguistics",
url = "https://aclanthology.org/2022.emnlp-tutorials.5",
pages = "23--29",
}