A easy venture walkthrough in becoming Generalised Linear Fashions in Python
Regardless of writing a number of articles on the subject and dealing within the insurance coverage business, I’ve truly by no means fitted a Generalised Linear Mannequin (GLM) from scratch.
Surprising I do know.
So, I’ve determined to unfold my wings and perform a small venture the place I can put all my theoretical information into practise!
On this article, I wish to stroll you thru a easy venture utilizing GLMs to mannequin the bicycle crossing volumes in New York Metropolis. We may even briefly cowl the principle technical particulars behind GLMs and the motivations for his or her use.
The information used for this venture was from the New York Metropolis Division of Transportation and is offered right here on Kaggle with a CC0 licence. Kaggle truly sourced this dataset fron NYC Open Information which you discover right here.
For the aim of completeness, I’ll talk about the principle ideas behind GLMs on this submit. Nonetheless, for a extra in-depth understanding, I extremely advocate you take a look at my earlier articles that basically deep-dive into their technical particulars:
Motivation
Generalised Linear Fashions actually ‘generalise’ Linear Regression to a goal variable that’s non-normal.
For instance, right here we’re going to be modelling the bicycle crossing volumes in New York Metropolis. If we have been going to mannequin this as a Linear Regression downside, we’d be assuming that the bicycle rely towards our options would observe a Regular distribution.
There are two points with this:
- Regular distribution is steady, whereas bicycle rely is discrete.
- Regular distribution may be unfavourable, however bicycle rely is optimistic.
Therefore, we use GLMs to beat these points and limitations of normal Linear Regression.
Arithmetic
The overall formulation for Linear Regression is:

The place X are the options, β are the coefficients with β_0 being the intercept and E[Y | X] is the anticipated worth (imply) of Y given our information X.
To rework this Linear Regression formulation to include non-normal distributions, we connect one thing referred to as the hyperlink perform, g():

The hyperlink perform actually ‘hyperlinks’ your linear mixture enter to your required goal distribution.
The hyperlink perform can both be discovered empirically or mathematically for every distribution. Within the articles I’ve linked above, I am going by way of deriving the hyperlink capabilities for some distributions.
Not each distibution is roofed underneath the GLM umbrella. The distributions should be a part of the exponential household. Nonetheless, most of your frequent distributions: Gamma, Poisson, Binomial and Bernoulli are all a part of this household.
The hyperlink perform for the Regular distribution (Linear Regression) is named the identification.
Poisson Regression
To mannequin our bicycle volumes we are going to use the Poisson distribution. This distribution describes the likelihood of a sure variety of occasions occurring in a given timeframe with a imply prevalence price.
To study extra concerning the Poisson distribution take a look at my article about it right here.
For Poisson Regression, the hyperlink perform is the pure log:
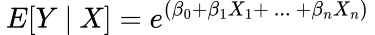
As you’ll be able to see, our output will now at all times be optimistic as we’re utilizing the exponential. This implies we are going to keep away from any doable non-sensical outcomes, in contrast to if we used Linear Regression the place the output might have been unfavourable.
Once more, I haven’t performed a full thorough evaluation of GLMs as it might be exhaustive and I’ve beforehand coated these matters. If you’re curious about studying extra about GLMs, be certain that to take a look at my articles I linked above or any of the hyperlinks I’ve supplied all through!
Packages
We’ll first obtain the fundamental Information Science packages and likewise the statsmodels package deal for GLM modelling.
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import statsmodels.api as sm
from statsmodels.formulation.api import glm
Information
Learn in and print the info:
information = pd.read_csv('nyc-east-river-bicycle-counts.csv')
information.head()

Right here we now have the bike volumes throughout the 4 bridges: Brooklyn, Manhattan, Williamsburg and Queensboro with their sum underneath the ‘Complete’ function.
There are duplicate columns for ‘Date’ and the index, so lets clear that up:
information.drop(['Unnamed: 0', 'Day'], axis=1, inplace=True)
information.head()

Discover there are two columns for temperature: excessive and low. Lets make {that a} single column by taking their imply:
information['Mean_Temp'] = (information['High Temp (°F)'] + information['Low Temp (°F)'])/2
information.head()

The precipitation column comprises some strings, so lets take away these:
information['Precipitation'].exchange(to_replace='0.47 (S)', worth=0.47, inplace=True)
information['Precipitation'].exchange(to_replace='T', worth=0, inplace=True)
information['Precipitation'] = information['Precipitation'].astype(np.float16)
information.head()

Visualisations
The 2 most important impartial variables that have an effect on bicycle volumes are temperature and precipitation. We will plot these two variables towards the goal variable ‘Complete’:
fig = plt.determine(figsize=(22,7))
ax = fig.add_subplot(121)
ax.scatter(information['Mean_Temp'], information['Total'], linewidth=4, colour='blue')
ax.tick_params(axis="x", labelsize=22)
ax.tick_params(axis="y", labelsize=22)
ax.set_xlabel('Imply Temperature', fontsize=22)
ax.set_ylabel('Complete Bikes', fontsize=22)
ax2 = fig.add_subplot(122)
ax2.scatter(information['Precipitation'], information['Total'], linewidth=4, colour='crimson')
ax2.tick_params(axis="x", labelsize=22)
ax2.tick_params(axis="y", labelsize=22)
ax2.set_xlabel('Precipitation', fontsize=22)
ax2.set_ylabel('Complete Bikes', fontsize=22)

Modelling
We will now construct a mannequin to foretell ‘Complete’ utilizing the imply temperature function by way of the statsmodel package deal. As this relationship is Poisson, we are going to use the pure log hyperlink perform:
mannequin = glm('Complete ~ Mean_Temp', information = information[['Total','Mean_Temp']], household = sm.households.Poisson())
outcomes = mannequin.match()
outcomes.abstract()

We used the R-style formulation for the GLM as that offers higher efficiency within the backend.
Evaluation
From the output above, we see that the coefficient for the imply temperature is 0.0263 and the intercept is 8.1461.
Utilizing the Poisson Regression formulation we introduced above, the equation of our line is then:

x = np.linspace(information['Mean_Temp'].min(),information['Mean_Temp'].max(),100)
y = np.exp(x*outcomes.params[1] + outcomes.params[0])plt.determine(figsize=(10,6))
plt.scatter(information['Mean_Temp'], information['Total'], linewidth=3, colour='blue')
plt.plot(x, y, label = 'Poisson Regression', colour='crimson', linewidth=3)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.xlabel('Imply Temperature', fontsize=18)
plt.ylabel('Complete Depend', fontsize=18 )
plt.legend(fontsize=18)
plt.present()

Eureka! We’ve got fitted a GLM!
For the reader, the algorithm utilized by statsmodels to suit the GLM is named iteratively reweighted least squares.
The complete code/pocket book is offered at my GitHub right here:
On this article we had a brief dialogue of the short-comings of Linear Regression and the way GLMs clear up this challenge by offering a wider and generic framework for regression fashions. We then match a primary Poisson Regression line to mannequin the variety of bicycles in New York Metropolis as a perform of each day common temperature.

