Introduction to Department and Certain – Knowledge Buildings and Algorithms Tutorial

Department and certain algorithms are used to search out the optimum answer for combinatory, discrete, and normal mathematical optimization issues.

A department and certain algorithm present an optimum answer to an NP-Laborious drawback by exploring the whole search area. By means of the exploration of the whole search area, a department and certain algorithm establish attainable candidates for options step-by-step.

There are numerous optimization issues in pc science, a lot of which have a finite variety of the possible shortest path in a graph or minimal spanning tree that may be solved in polynomial time. Usually, these issues require a worst-case state of affairs of all attainable permutations. The department and certain algorithm create branches and bounds for one of the best answer.

On this tutorial, we’ll focus on the department and certain methodology intimately.

Introduction to Department and Certain

When to use Department and Certain Algorithm?

Department and certain is an efficient answer to some issues, which we’ve got already mentioned. We’ll focus on all such instances the place branching and binding are applicable on this part.

• It’s applicable to make use of a department and certain method if the given drawback is discrete optimization. Discrete optimization refers to issues during which the variables belong to the discrete set. Examples of such issues embrace 0-1 Integer Programming and Community Move issues.
• Relating to combinatory optimization issues, department and certain work effectively. An optimization drawback is optimized by combinatory optimization by discovering its most or minimal based mostly on its goal operate. The combinatory optimization issues embrace Boolean Satisfiability and Integer Linear Programming.

Forms of Department and Certain Options:

The answer of the Department and the certain drawback might be represented in two methods:

• Variable measurement answer: Utilizing this answer, we will discover the subset of the given set that provides the optimized answer to the given drawback. For instance, if we’ve got to pick out a mixture of parts from {A, B, C, D} that optimizes the given drawback, and it’s discovered that A and B collectively give one of the best answer, then the answer will likely be {A, B}.
• Fastened-size answer: There are 0s and 1s on this answer, with the digit on the ith place indicating whether or not the ith component ought to be included, for the above instance, the answer will likely be given by {1, 1, 0, 0}, right here 1 characterize that we’ve got choose the component which at ith place and 0 characterize we don’t choose the component at ith place.

Classification of Department and Certain Issues:

The Department and Certain methodology might be labeled into three sorts based mostly on the order during which the state area tree is searched. 

1. FIFO Department and Certain
2. LIFO Department and Certain
3. Least Price-Department and Certain

We are going to now focus on every of those strategies in additional element. To indicate the options in these strategies, we’ll use the variable answer methodology.

1. FIFO Department and Certain

First-In-First-Out is an method to the department and certain drawback that makes use of the queue method to create a state-space tree. On this case, the breadth-first search is carried out, that’s, the weather at a sure stage are all searched, after which the weather on the subsequent stage are searched, beginning with the primary little one of the primary node on the earlier stage.

For a given set {A, B, C, D}, the state area tree will likely be constructed as follows :

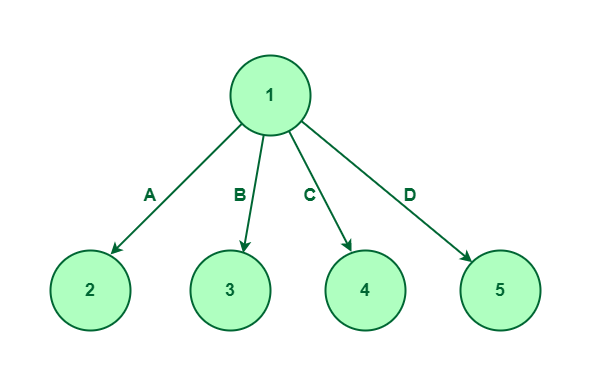
State House tree for set {A, B, C, D}

The above diagram exhibits that we first take into account component A, then component B, then component C and eventually we’ll take into account the final component which is D. We’re performing BFS whereas exploring the nodes.

So, as soon as the primary stage is accomplished. We’ll take into account the primary component, then we will take into account both B, C, or D. If we observe the route then it says that we’re doing parts A and D so we won’t take into account parts B and C. If we choose the weather A and D solely, then it says that we’re deciding on parts A and D and we aren’t contemplating parts B and C.

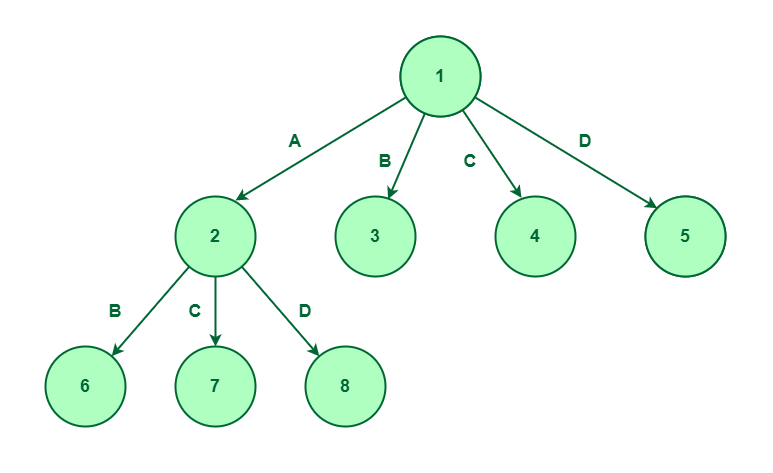
Choosing component A

Now, we’ll increase node 3, as we’ve got thought of component B and never thought of component A, so, we’ve got two choices to discover that’s parts C and D. Let’s create nodes 9 and 10 for parts C and D respectively.

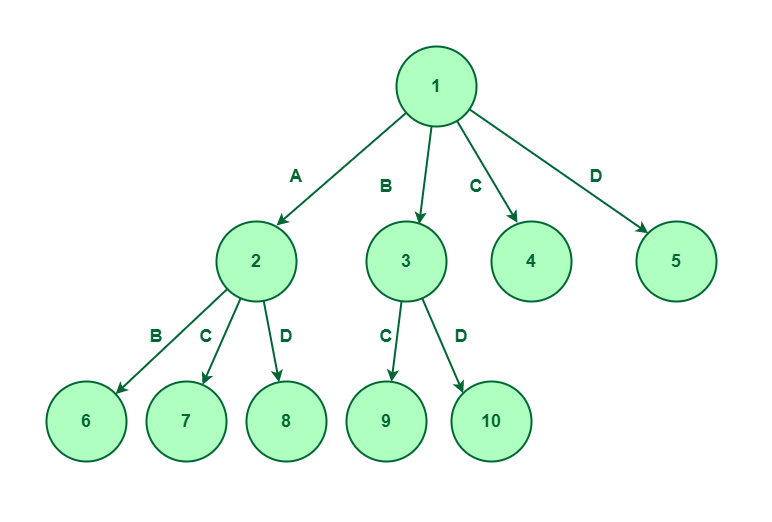
Thought of component B and never thought of component A

Now, we’ll increase node 4 as we’ve got solely thought of parts C and never thought of parts A and B, so, we’ve got just one choice to discover which is component  D. Let’s create node 11 for D.

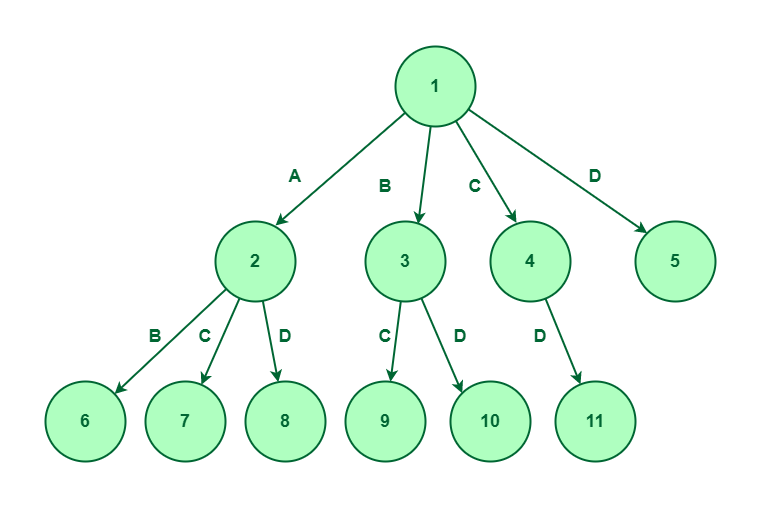
 Thought of parts C and never thought of parts A and B

Until node 5, we’ve got solely thought of parts D, and never chosen parts A, B, and C. So, We now have no extra parts to discover, Due to this fact on node 5, there received’t be any enlargement.

Now, we’ll increase node 6 as we’ve got thought of parts A and B, so, we’ve got solely two choice to discover that’s component C and D. Let’s create node 12 and 13 for C and D respectively.

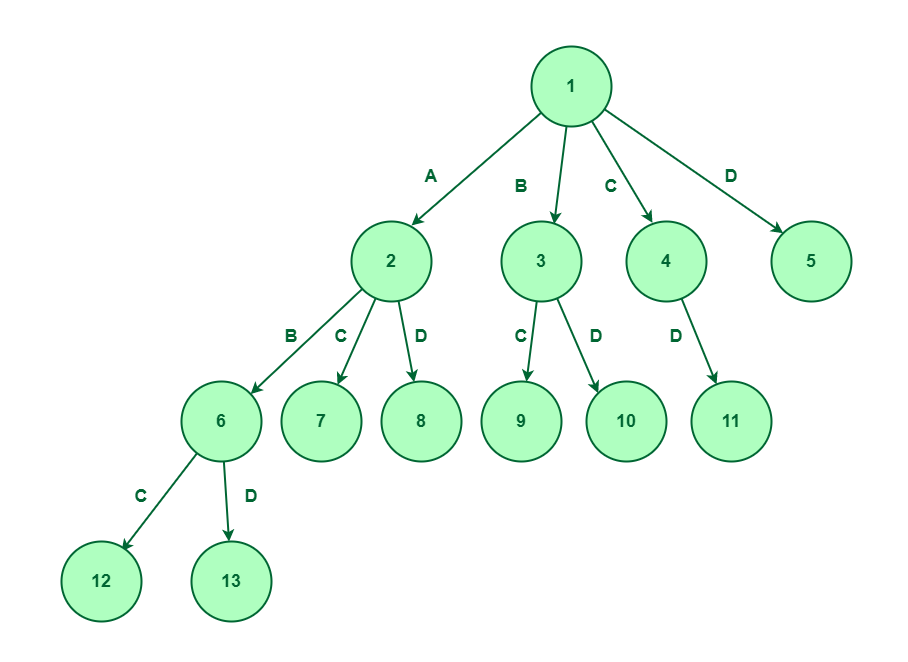
Develop node 6

Now, we’ll increase node 7 as we’ve got thought of parts A and C and never take into account component B, so, we’ve got just one choice to discover which is component  D. Let’s create node 14 for D.

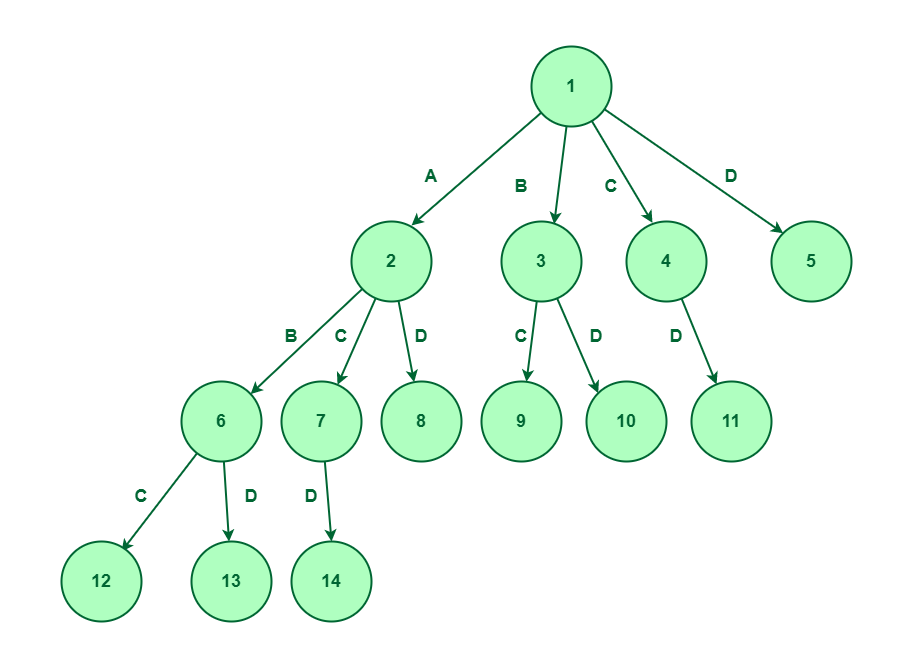
Develop node 7

Until node 8, we’ve got thought of parts A and D, and never chosen parts B and C, So, We now have no extra parts to discover, Due to this fact on node 8, there received’t be any enlargement.

Now, we’ll increase node 9 as we’ve got thought of parts B and C and never thought of component A, so, we’ve got just one choice to discover which is component  D. Let’s create node 15 for D.

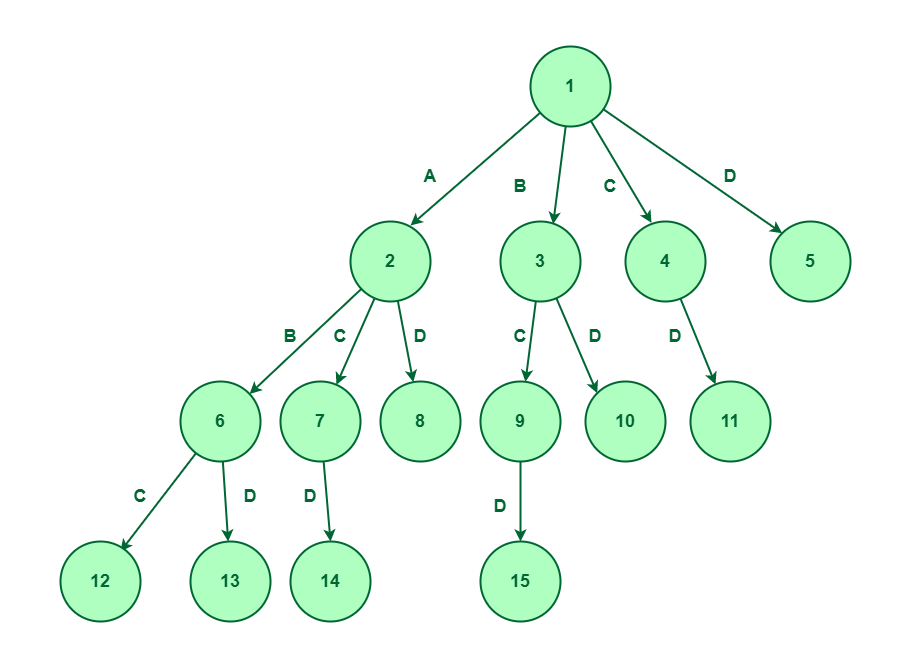
Develop node 9

2. LIFO Department and Certain

The Final-In-First-Out method for this drawback makes use of stack in creating the state area tree. When nodes are added to a state area tree, they’re added to a stack. In any case nodes of a stage have been added, we pop the topmost component from the stack and discover it.

For a given set {A, B, C, D}, the state area tree will likely be constructed as follows :

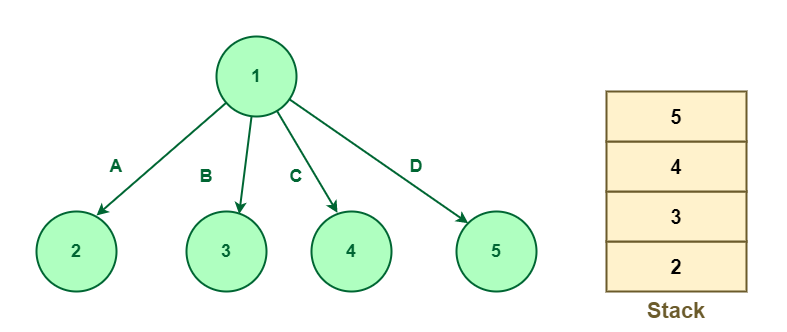
State area tree for component {A, B, C, D}

Now the enlargement can be based mostly on the node that seems on the highest of the stack. Since node 5 seems on the highest of the stack, so we’ll increase node 5. We are going to come out node 5 from the stack. Since node 5 is within the final component, i.e., D so there isn’t a additional scope for enlargement.

The following node that seems on the highest of the stack is node 4. Pop-out node 4 and increase. On enlargement, component D will likely be thought of and node 6 will likely be added to the stack proven beneath:

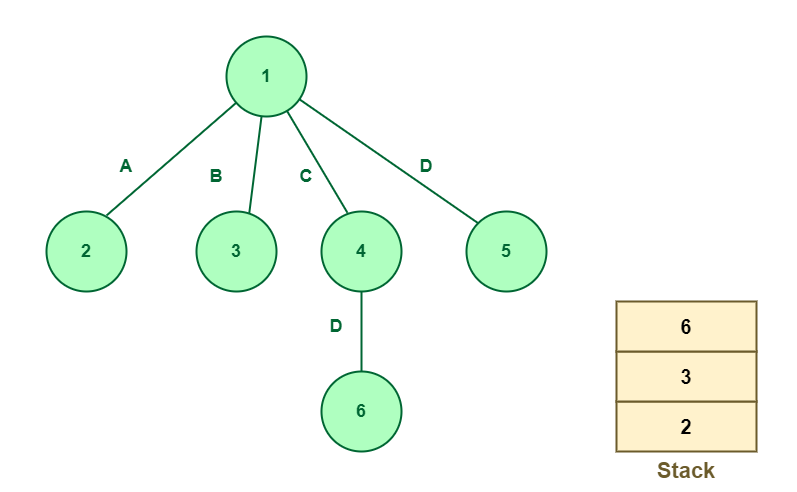
Develop node 4

The following node is 6 which is to be expanded. Pop-out node 6 and increase. Since node 6 is within the final component, i.e., D so there isn’t a additional scope for enlargement.

The following node to be expanded is node 3. Since node 3 works on component B so node 3 will likely be expanded to 2 nodes, i.e., 7 and eight engaged on parts C and D respectively. Nodes 7 and eight will likely be pushed into the stack.

The following node that seems on the highest of the stack is node 8. Pop-out node 8 and increase. Since node 8 works on component D so there isn’t a additional scope for the enlargement.

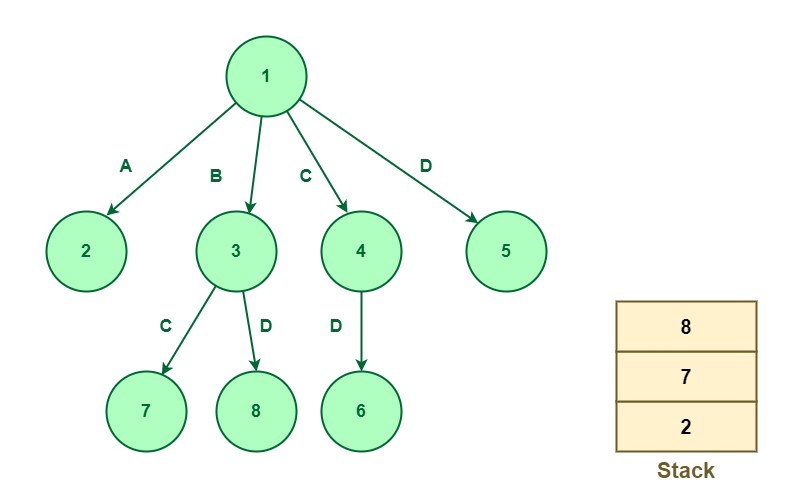
Develop node 3

The following node that seems on the highest of the stack is node 7. Pop-out node 7 and increase. Since node 7 works on component C so node 7 will likely be additional expanded to node 9 which works on component D and node 9 will likely be pushed into the stack.

The following node is 6 which is to be expanded. Pop-out node 6 and increase. Since node 6 is within the final component, i.e., D so there isn’t a additional scope for enlargement.

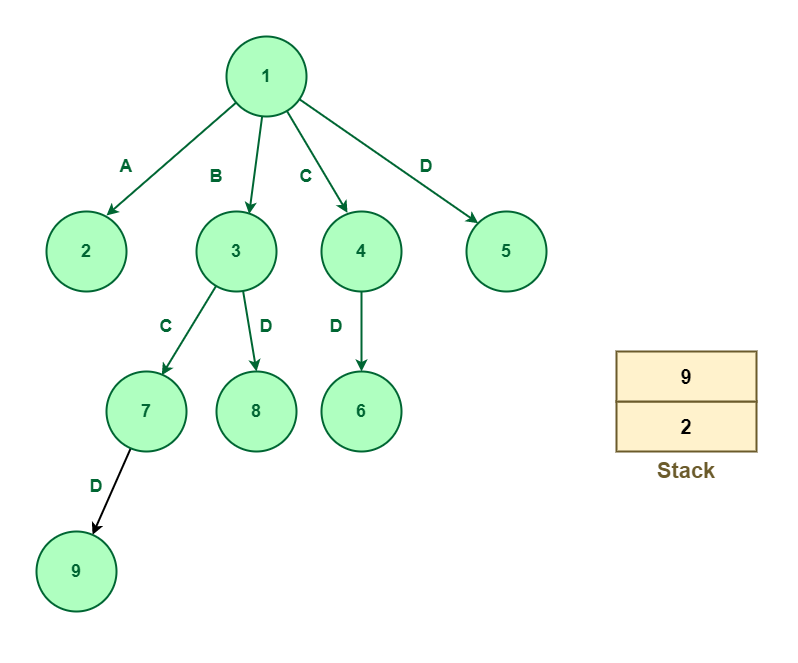
Develop node 7

The following node that seems on the highest of the stack is node 9. Since node 9 works on component D, there isn’t a additional scope for enlargement.

The following node that seems on the highest of the stack is node 2. Since node 2 works on the component A so it signifies that node 2 might be additional expanded. It may be expanded as much as three nodes named 10, 11, 12 engaged on parts B, C, and D respectively. There new nodes will likely be pushed into the stack proven as beneath:

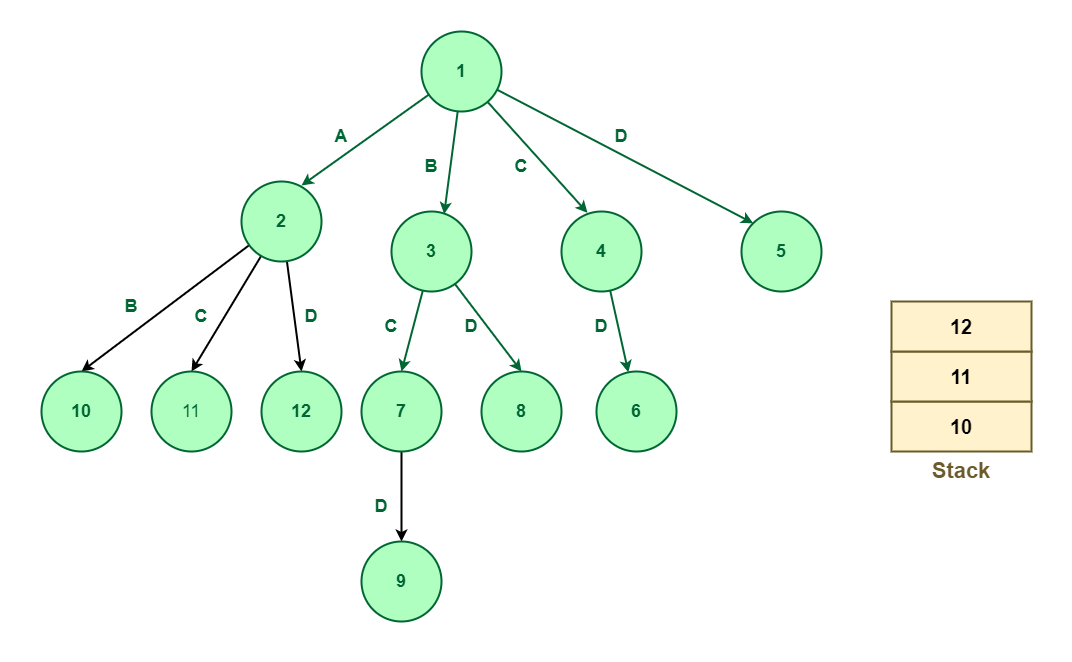
Develop node 2

Within the above methodology, we explored all of the nodes utilizing the stack that follows the LIFO precept.

3. Least Price-Department and Certain

To discover the state area tree, this methodology makes use of the fee operate. The earlier two strategies additionally calculate the fee operate at every node however the fee shouldn’t be been used for additional exploration.

On this approach, nodes are explored based mostly on their prices, the price of the node might be outlined utilizing the issue and with the assistance of the given drawback, we will outline the fee operate. As soon as the fee operate is outlined, we will outline the price of the node.
Now, Think about a node whose value has been decided. If this worth is bigger than U0, this node or its kids will be unable to provide an answer. Because of this, we will kill this node and never discover its additional branches. Because of this, this methodology prevents us from exploring instances that aren’t price it, which makes it extra environment friendly for us. 

Let’s first take into account node 1 having value infinity proven beneath:

Within the following diagram, node 1 is expanded into 4 nodes named 2, 3, 4, and 5.

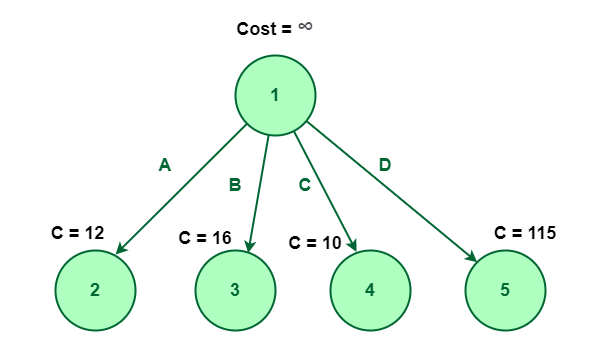
Node 1 is expanded into 4 nodes named 2, 3, 4, and 5

Assume that value of the nodes 2, 3, 4, and 5 are 12, 16, 10, and 315 respectively.
On this methodology, we’ll discover the node which is having the least value. Within the above determine, we will observe that the node with a minimal value is node 4. So, we’ll discover node 4 having a price of 10.

Throughout exploring node 4 which is component C, we will discover that there’s just one attainable component that is still unexplored which is D (i.e, we already determined to not choose parts A, and B). So, it can get expanded to at least one single component D, let’s say this node quantity is 6.

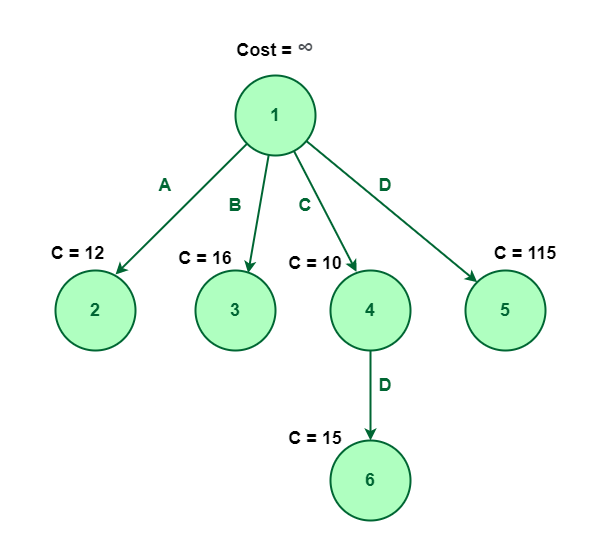
Exploring node 4 which is component C

Now, Node 6 has no component left to discover. So, there isn’t a additional scope for enlargement. Therefore the component {C, D} is the optimum approach to decide on for the least value.

Issues that may be solved utilizing Department and Certain Algorithm:

The Department and Certain methodology can be utilized for fixing most combinatorial issues. A few of these issues are given beneath: