Introduction to Bitwise Algorithms – Information Buildings and Algorithms Tutorial

October 11, 2022

1

Bit stands for binary digit. A bit is the essential unit of data and might solely have considered one of two potential values that’s 0 or 1.

In our world, we often with numbers utilizing the decimal base. In different phrases. we use the digit 0 to 9 Nonetheless, there are different quantity representations that may be fairly helpful such because the binary quantity techniques.

Introduction to Bitwise Algorithms - Data Structures and Algorithms Tutorial

Introduction to Bitwise Algorithms – Information Buildings and Algorithms Tutorial

Not like people, computer systems don’t have any ideas of phrases and numbers. They obtain information encoded on the lowest stage as a sequence of zeros and ones (0 and 1). These are known as bits, and they’re the foundation for all of the instructions they obtain. We’ll start by studying about bits after which discover a number of algorithms for manipulating bits. We’ll then discover a number of algorithms for manipulating bits. The tutorial is supposed to be an introduction to bit algorithms for programmers.

Fundamentals of Bit manipulation (Bitwise Operators)

An algorithmic operation referred to as bit manipulation entails the manipulation of bits on the bit stage (bitwise). Bit manipulation is all about these bitwise operations. They enhance the effectivity of packages by being primitive, quick actions.

The pc makes use of this bit manipulation to carry out operations like addition, subtraction, multiplication, and division are all executed on the bit stage. This operation is carried out within the arithmetic logic unit (ALU) which is part of a pc’s CPU. Contained in the ALU, all such mathematical operations are carried out.

There are completely different bitwise operations used within the bit manipulation. These bit operations function on the person bits of the bit patterns. Bit operations are quick and can be utilized in optimizing time complexity. Some widespread bit operators are:

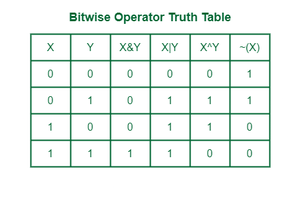
Bitwise Operator Reality Desk

1. Bitwise AND Operator (&)

The bitwise AND operator is denoted utilizing a single ampersand image, i.e. &. The & operator takes two equal-length bit patterns as parameters. The 2-bit integers are in contrast. If the bits within the in contrast positions of the bit patterns are 1, then the ensuing bit is 1. If not, it’s 0.

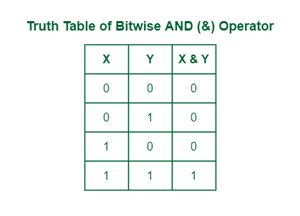
Reality desk of AND operator

Instance:

Take two bit values X and Y, the place X = 7= (111)₂ and Y = 4 = (100)₂. Take Bitwise and of each X & y

Bitwise ANDof (7 & 4)

Implementation of AND operator:

C++

#embody <bits/stdc++.h>

utilizing namespace std;

int predominant()

{

int a = 7, b = 4;

int outcome = a & b;

cout << outcome << endl;

return 0;

}

2 Bitwise OR Operator (|)

The | Operator takes two equal size bit designs as boundaries; if the 2 bits within the looked-at place are 0, the following bit is zero. If not, it’s 1.

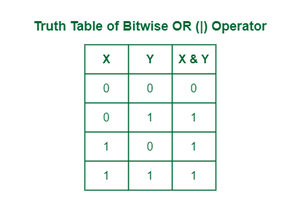
Reality desk of OR operator

Instance:

Take two bit values X and Y, the place X = 7= (111)₂ and Y = 4 = (100)₂. Take Bitwise and of each X & y

Bitwise OR of (7 | 4)

Explaination: On the premise of reality desk of bitwise OR operator we are able to conclude that the results of

1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0

We used the same idea of bitwise operator which might be present within the picture.

Implementation of OR operator:

C++

#embody <bits/stdc++.h>

utilizing namespace std;

int predominant()

b;

cout << outcome;

return 0;

3. Bitwise XOR Operator (^)

The ^ operator (also called the XOR operator) stands for Unique Or. Right here, if bits within the in contrast place don’t match their ensuing bit is 1. i.e, The results of the bitwise XOR operator is 1 if the corresponding bits of two operands are reverse, in any other case 0.

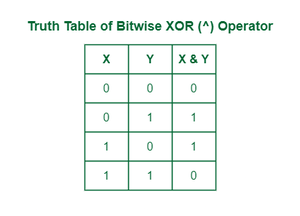
Reality Desk of Bitwise Operator XOR

Instance:

Take two bit values X and Y, the place X = 7= (111)₂ and Y = 4 = (100)₂. Take Bitwise and of each X & y

Bitwise OR of (7 ^ 4)

Explaination: On the premise of reality desk of bitwise XOR operator we are able to conclude that the results of

1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0

We used the same idea of bitwise operator which might be present within the picture.

Implementation of XOR operator:

C++

#embody <iostream>

utilizing namespace std;

int predominant()

{

int a = 12, b = 25;

cout << (a ^ b);

return 0;

}

4. Bitwise NOT Operator (!~)

All of the above three bitwise operators are binary operators (i.e, requiring two operands to be able to function). Not like different bitwise operators, this one requires just one operand to function.

The bitwise Not Operator takes a single worth and returns its one’s complement. The one’s complement of a binary quantity is obtained by toggling all bits in it, i.e, reworking the 0 bit to 1 and the 1 bit to 0.

Reality Desk of Bitwise Operator NOT

Instance:

Take two bit values X and Y, the place X = 5= (101)₂. Take Bitwise NOT of X.

Explaination: On the premise of reality desk of bitwise NOT operator we are able to conclude that the results of

~1 = 0
~0 = 1

We used the same idea of bitwise operator which might be present within the picture.

Implementation of NOT operator:

C++

#embody <iostream>

utilizing namespace std;

int predominant()

{

int a = 0;

cout << "Worth of a with out utilizing NOT operator: " << a;

cout << "nInverting utilizing NOT operator (with signal bit): " << (~a);

cout << "nInverting utilizing NOT operator (with out signal bit): " << (!a);

return 0;

}

Output

Worth of a with out utilizing NOT operator: 0
Inverting utilizing NOT operator (with signal bit): -1
Inverting utilizing NOT operator (with out signal bit): 1

5. Left-Shift (<<)

The left shift operator is denoted by the double left arrow key (<<). The overall syntax for left shift is shift-expression << okay. The left-shift operator causes the bits in shift expression to be shifted to the left by the variety of positions specified by okay. The bit positions that the shift operation has vacated are zero-filled.

Word: Each time we shift a quantity in direction of the left by 1 bit it multiply that quantity by 2.

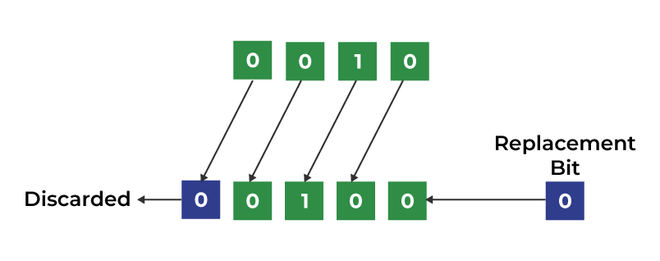
Left-Shift Bitwise Operator

Instance:

Enter: Left shift of 5 by 1.
Binary illustration of 5 = 00101 and Left shift of 00101₂ by 1 (i.e, 00101 << 1)

Left shif of 5 by 1

Output: 10
Explaination: All little bit of 5 will likely be shifted by 1 to left facet and this end in 01010_2,Which is equal to 10

Enter: Left shift of 5 by 2.
Binary illustration of 5 = 00101 and Left shift of 00101₂ by 1 (i.e, 00101 << 2)

Left shif of 5 by 2

Output: 20
Explaination: All little bit of 5 will likely be shifted by 1 to left facet and this end in 10100_2,Which is equal to twenty

Enter: Left shift of 5 by 3.
Binary illustration of 5 = 00101 and Left shift of 00101₂ by 1 (i.e, 00101 << 3)

Left shif of 5 by 3

Output: 40
Explaination: All little bit of 5 will likely be shifted by 1 to left facet and this end in 01000_2,Which is equal to 40

Implementation of Left shift operator:

C++

#embody <bits/stdc++.h>

utilizing namespace std;

int predominant()

{

unsigned int num1 = 1024;

bitset<32> bt1(num1);

cout << bt1 << endl;

unsigned int num2 = num1 << 1;

bitset<32> bt2(num2);

cout << bt2 << endl;

unsigned int num3 = num1 << 2;

bitset<16> bitset13{ num3 };

cout << bitset13 << endl;

}

Output

00000000000000000000010000000000
00000000000000000000100000000000
0001000000000000

6. Proper-Shift (>>)

The correct shift operator is denoted by the double proper arrow key (>>). The overall syntax for the proper shift is “shift-expression >> okay”. The correct-shift operator causes the bits in shift expression to be shifted to the proper by the variety of positions specified by okay. For unsigned numbers, the bit positions that the shift operation has vacated are zero-filled. For signed numbers, the signal bit is used to fill the vacated bit positions. In different phrases, if the quantity is constructive, 0 is used, and if the quantity is destructive, 1 is used.

Word: Each time we shift a quantity in direction of the proper by 1 bit it divides that quantity by 2.

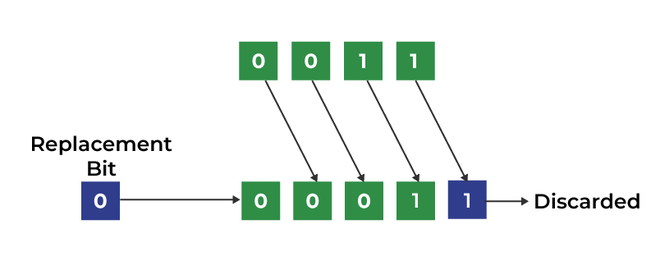
Proper-Shift Operator

Instance:

Enter: Left shift of 5 by 1.
Binary illustration of 5 = 00101 and Left shift of 00101₂ by 1 (i.e, 00101 << 1)

Rightshif of 5 by 1

Output: 10
Explaination: All little bit of 5 will likely be shifted by 1 to left facet and this end in 01010_2,Which is equal to 10

Enter: Left shift of 5 by 2.
Binary illustration of 5 = 00101 and Left shift of 00101₂ by 1 (i.e, 00101 << 2)

Proper shif of 5 by 2

Output: 20
Explaination: All little bit of 5 will likely be shifted by 1 to left facet and this end in 10100_2,Which is equal to twenty

Enter: Left shift of 5 by 3.
Binary illustration of 5 = 00101 and Left shift of 00101₂ by 1 (i.e, 00101 << 3)

Proper shif of 5 by 3

Output: 40
Explaination: All little bit of 5 will likely be shifted by 1 to left facet and this end in 01000_2,Which is equal to 40

Implementation of Proper shift operator:

C++

#embody <bitset>

#embody <iostream>

utilizing namespace std;

int predominant()

{

unsigned int num1 = 1024;

bitset<32> bt1(num1);

cout << bt1 << endl;

unsigned int num2 = num1 >> 1;

bitset<32> bt2(num2);

cout << bt2 << endl;

unsigned int num3 = num1 >> 2;

bitset<16> bitset13{ num3 };

cout << bitset13 << endl;

}

Output

00000000000000000000010000000000
00000000000000000000001000000000
0000000100000000

Software of BIT Operators

Bit operations are used for the optimization of embedded techniques.
The Unique-or operator can be utilized to verify the integrity of a file, ensuring it has not been corrupted, particularly after it has been in transit.
Bitwise operations are utilized in Information encryption and compression.
Bits are used within the space of networking, framing the packets of quite a few bits that are despatched to a different system usually via any sort of serial interface.
Digital Picture Processors use bitwise operations to boost picture pixels and to extract completely different sections of a microscopic picture.

Necessary Apply Issues on Bitwise Algorithm:

1. The way to Set a bit within the quantity?

If we wish to set a bit at nth place within the quantity ‘num’, it may be executed utilizing the ‘OR’ operator( | ).

First, we left shift 1 to n place by way of (1<<n)
Then, use the “OR” operator to set the bit at that place. “OR” operator is used as a result of it is going to set the bit even when the bit is unset beforehand within the binary illustration of the quantity ‘num’.

Word: If the bit can be already set then it might stay unchanged.

Under is the implementation:

C++

#embody <iostream>

utilizing namespace std;

void set(int& num, int pos)

= (1 << pos);

int predominant()

{

int num = 4, pos = 1;

set(num, pos);

cout << (int)(num) << endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static void predominant(String[] args)

{

int num = 4, pos = 1;

num = set(num, pos);

System.out.println(num);

}

public static int set(int num, int pos)

= (1 << pos);

return num;

}

Python3

def set(num, pos):

num |= (1 << pos)

print(num)

num, pos = 4, 1

set(num, pos)

C#

utilizing System;

public class GFG {

static public void Important()

{

int num = 4, pos = 1;

set(num, pos);

}

static public void set(int num, int pos)

= (1 << pos);

Console.WriteLine(num);

}

Javascript

<script>

perform set(num,pos)

= (1 << pos);

console.log(parseInt(num));

let num = 4;

let pos = 1;

set(num, pos);

</script>

2. The way to unset/clear a bit at n’th place within the quantity

Suppose we wish to unset a bit at nth place in quantity ‘num’ then we’ve got to do that with the assistance of “AND” (&) operator.

First, we left shift ‘1’ to n place by way of (1<<n) then we use bitwise NOT operator ‘~’ to unset this shifted ‘1’.
Now after clearing this left shifted ‘1’ i.e making it to ‘0’ we are going to ‘AND'(&) with the quantity ‘num’ that may unset bit at nth place.

Under is the implementation:

C++

#embody <iostream>

utilizing namespace std;

void unset(int& num, int pos)

{

num &= (~(1 << pos));

}

int predominant()

{

int num = 7;

int pos = 1;

unset(num, pos);

cout << num << endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static void predominant(String[] args)

{

int num = 7, pos = 1;

num = unset(num, pos);

System.out.println(num);

}

public static int unset(int num, int pos)

{

num = num & (~(1 << pos));

return num;

}

Python3

def unset(num, pos):

num &= (~(1 << pos))

print(num)

num, pos = 7, 1

unset(num, pos)

C#

utilizing System;

public class GFG {

static public void Important()

{

int num = 7, pos = 1;

unset(num, pos);

}

static public void unset(int num, int pos)

{

num &= (~(1 << pos));

Console.WriteLine(num);

}

3. Toggling a bit at nth place

Toggling means to show bit ‘on'(1) if it was ‘off'(0) and to show ‘off'(0) if it was ‘on'(1) beforehand. We will likely be utilizing the ‘XOR’ operator right here which is that this ‘^’. The explanation behind the ‘XOR’ operator is due to its properties.

Properties of ‘XOR’ operator.
- 1^1 = 0
- 0^0 = 0
- 1^0 = 1
- 0^1 = 1
If two bits are completely different then the ‘XOR’ operator returns a set bit(1) else it returns an unset bit(0).

Under is the implementation:

C++

#embody <iostream>

utilizing namespace std;

void toggle(int& num, int pos) { num ^= (1 << pos); }

int predominant()

{

int num = 4;

int pos = 1;

toggle(num, pos);

cout << num << endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static void predominant(String[] args)

{

int num = 4, pos = 1;

num = toggle(num, pos);

System.out.println(num);

}

public static int toggle(int num, int pos)

{

num ^= (1 << pos);

return num;

}

Python3

def toggle(num, pos):

num ^= (1 << pos)

print(num)

num, pos = 4, 1

toggle(num, pos)

C#

utilizing System;

public class GFG {

static public void Important()

{

int num = 4, pos = 1;

toggle(num, pos);

}

static public void toggle(int num, int pos)

{

num ^= (1 << pos);

Console.WriteLine(num);

}

4. Checking if the bit at nth place is Set or Unset

We used the left shift (<<) operation on 1 to shift the bits to nth place after which use the & operation with quantity given quantity, and verify whether it is not-equals to 0.

Under is the implementation:

C++

#embody <iostream>

utilizing namespace std;

bool at_position(int num, int pos)

{

bool bit = num & (1 << pos);

return bit;

}

int predominant()

{

int num = 5;

int pos = 2;

bool bit = at_position(num, pos);

cout << bit << endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static void predominant(String[] args)

{

int num = 5;

int pos = 0;

int bit = at_position(num, pos);

System.out.println(bit);

}

public static int at_position(int num, int pos)

{

int bit = num & (1 << pos);

return bit;

}

Python3

def at_position(num, pos):

bit = num & (1 << pos)

return bit

num = 5

pos = 0

bit = at_position(num, pos)

print(bit)

Javascript

<script>

perform at_position(num,pos)

{

return num & (1<<pos);

}

let num = 5;

let pos = 0;

console.log(at_position(num, pos));

</script>

5. Multiply a quantity by 2 utilizing the left shift operator

Under is the implementation:

C++

#embody <iostream>

utilizing namespace std;

int predominant()

{

int num = 12;

int ans = num << 1;

cout << ans << endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static void predominant(String[] args)

{

int num = 12;

int ans = num << 1;

System.out.println(ans);

}

C#

utilizing System;

public class GFG {

static public void Important()

{

int num = 12;

Console.WriteLine(num << 1);

}

Python3

num = 12

ans = num << 1

print(ans)

Javascript

<script>

var num = 12;

var ans = num<<1;

doc.write(ans);

</script>

6. Divide a quantity 2 utilizing the proper shift operator

Under is the implementation:

C++

#embody <iostream>

utilizing namespace std;

int predominant()

{

int num = 12;

int ans = num >> 1;

cout << ans << endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static void predominant(String[] args)

{

int num = 12;

int ans = num >> 1;

System.out.println(ans);

}

C#

utilizing System;

public class GFG {

static public void Important()

{

int num = 12;

Console.WriteLine(num >> 1);

}

Python3

num = 12

ans = num >> 1

print(ans)

Javascript

<script>

var num = 12;

var ans = num>>1;

doc.write(ans);

</script>

7. Compute XOR from 1 to n (direct technique)

The drawback may be solved based mostly on the next observations:

Say x = n % 4. The XOR worth depends upon the worth if x.

If, x = 0, then the reply is n.
x = 1, then reply is 1.
x = 2, then reply is n+1.
x = 3, then reply is 0.

Under is the implementation of the above strategy.

C++

int computeXOR(int n)

{

if (n % 4 == 0)

return n;

if (n % 4 == 1)

return 1;

if (n % 4 == 2)

return n + 1;

else

return 0;

}

Java

import java.io.*;

class GFG {

public static int computeXOR(int n)

{

if (n % 4 == 0)

return n;

if (n % 4 == 1)

return 1;

if (n % 4 == 2)

return n + 1;

else

return 0;

}

public static void predominant(String[] args) {}

}

Python

def set(num, pos):

num |= (1 << pos)

print(num)

num, pos = 4, 1

set(num, pos)

C#

utilizing System;

public class GFG {

public static int computeXOR(int n)

{

if (n % 4 == 0)

return n;

if (n % 4 == 1)

return 1;

if (n % 4 == 2)

return n + 1;

else

return 0;

}

public static void Important() {}

}

Javascript

<script>

perform computeXOR(n)

{

if (n % 4 == 0)

return n;

if (n % 4 == 1)

return 1;

if (n % 4 == 2)

return n + 1;

else

return 0;

}

</script>

8. The way to know if a quantity is an influence of two?

This may be solved based mostly on the next reality:

If a quantity N is an influence of two, then the bitwise AND of N and N-1 will likely be 0. However this is not going to work if N is 0. So simply verify these two circumstances, if any of those two circumstances is true.

Under is the implementation of the above strategy.

C++

bool isPowerOfTwo(int x)

{

return x && (!(x & (x - 1)));

}

Python

def isPowerOfTwo(x):

return x and (not(x & (x - 1)))

C#

utilizing System;

public class GFG {

static public bool isPowerOfTwo(int x)

{

return (x != 0) && ((x & (x - 1)) == 0);

}

static public void Important() {}

}

9. Rely Set bits in an integer

Counting set bits means, counting whole variety of 1’s within the binary illustration of an integer. For this drawback we undergo all of the bits of given quantity and verify whether or not it’s set or not by performing AND operation (with 1).

Under is the implementation:

C++

int countBits(int n)

{

int rely = 0;

whereas (n) {

rely += n & 1;

n >>= 1;

}

return rely;

}

10. Place of rightmost set bit

The concept is to unset the rightmost little bit of quantity n and XOR the outcome with n. Then the rightmost set bit in n would be the place of the one set bit within the outcome. Word that if n is odd, we are able to instantly return 1 as the primary bit is all the time set for odd numbers.

Instance:
The quantity 20 in binary is 00010100, and the place of the rightmost set bit is 3.

00010100 & (n = 20)
00010011 (n-1 = 19)
——————-
00010000 ^ (XOR outcome quantity with n)
00010100
——————-
00000100 ——-> rightmost set bit will inform us the place

Under is the implementation:

C++

int positionOfRightmostSetBit(int n)

{

if (n & 1) {

return 1;

}

n = n ^ (n & (n - 1));

int pos = 0;

whereas (n) {

n = n >> 1;

pos++;

}

return pos;

}

Java

public static int positionOfRightmostSetBit(int n)

{

if ((n & 1) != 0) {

return 1;

}

n = n ^ (n & (n - 1));

int pos = 0;

whereas (n != 0) {

n = n >> 1;

pos++;

}

return pos;

}

Python

def positionOfRightmostSetBit(n):

if n & 1:

return 1

n = n ^ (n & (n - 1))

pos = 0

whereas n:

n = n >> 1

pos = pos + 1

return pos

Associated article:

Previous articleHow Xdebug Can Assist You Grow to be a Higher WordPress Developer

Introduction to Bitwise Algorithms – Information Buildings and Algorithms Tutorial

Fundamentals of Bit manipulation (Bitwise Operators)

1. Bitwise AND Operator (&)

C++

2 ​Bitwise OR Operator (|)

C++

3. ​Bitwise XOR Operator (^)

C++

4. ​Bitwise NOT Operator (!~)

C++

5. Left-Shift (<<)

C++

6. Proper-Shift (>>)

C++

Software of BIT Operators

Necessary Apply Issues on Bitwise Algorithm:

1. The way to Set a bit within the quantity?

C++

Java

Python3

C#

Javascript

2. The way to unset/clear a bit at n’th place within the quantity

C++

Java

Python3

C#

3. Toggling a bit at nth place

C++

Java

Python3

C#

4. Checking if the bit at nth place is Set or Unset

C++

Java

Python3

Javascript

5. Multiply a quantity by 2 utilizing the left shift operator

C++

Java

C#

Python3

Javascript

6. Divide a quantity 2 utilizing the proper shift operator

C++

Java

C#

Python3

Javascript

7. Compute XOR from 1 to n (direct technique)

C++

Java

Python

C#

Javascript

8. The way to know if a quantity is an influence of two?

C++

Python

C#

9. Rely Set bits in an integer

C++

10. Place of rightmost set bit

C++

Java

Python

LEAVE A REPLY Cancel reply

Most Popular

Recent Comments

ABOUT US

POPULAR POSTS

POPULAR CATEGORY

2 Bitwise OR Operator (|)

3. Bitwise XOR Operator (^)

4. Bitwise NOT Operator (!~)