An introduction and a case research

As defined in my earlier put up, the framework of SHAP values, broadly used for machine studying explainability has sadly did not replicate the informal construction in its outcomes. Researchers have been proposing attainable options to take away such a limitation. Within the article, I can be reviewing one of many proposed alternate options, the Causal SHAP values (CSVs), and provides a easy instance with detailed computation as an example the distinction between CSVs and the “conventional” SHAP values.
Allow us to begin by recalling the definition of SHAP values, a way primarily based on cooperative sport idea, aiming to interpret a machine studying mannequin, attributing characteristic significance because the payoff {that a} characteristic has contributed to the ultimate output. For a given mannequin f, the SHAP worth of a characteristic x_j with j∈{1,2,…n}:=N in consideration is given by

the place π is a permutation of N which is chosen to be a uniform distribution and the image <π and ≤π characterize the indices that precede and precede or equal to a given index within the permutation.
We are able to discover instantly that the above computation is predicated on a marginal expectation, which, explains why SHAP values can’t replicate the causal relation of the mannequin.
Definition of CSVs
Think about a quite simple case the place characteristic 1 is the direct reason for characteristic 2 and we wish to argue that we can’t give the 2 options the identical weight when evaluating their contributions to the output of the mannequin. By instinct, the trigger must be thought of extra necessary than the impact when attributing characteristic significance. Such instinct results in the causal SHAP values (CSVs) framework, proposed by Heskes et al., aiming to change the present SHAP values framework with out breaking its fascinating properties, i.e. effectivity, symmetry, dummy, and additivity.
The CSVs has the next definition:

and we discover instantly the distinction from the previous definition (as much as a continuing in line with authors’ desire): the marginal expectation is changed by an interventional expectation realized by Pearl’s do-calculus. For individuals who should not accustomed to the idea, merely notice that the do(.) is a mathematical operator that enables us to conduct interventions in an off-the-cuff mannequin, often represented by a directed acyclic graph (DAG) and this “do” might be understood actually as “do it”. Based mostly on the definition of the CSVs, allow us to look again on the instance above: doing characteristic 1, the worth of characteristic 2 is now not free and the cause-and-effect could be taken into consideration by the interventional expectation.
Distinction from SHAP
Omitting particulars of computation, we wish to point out that the CSVs of a characteristic x_i might be decomposed into two elements: the direct contribution and the oblique contribution. The direct contribution is the change in prediction when the characteristic variable X_i takes the worth of the characteristic x_i whereas the oblique contribution is the change as a result of intervention do(X_i=x_i). On this sense, the distinction between CSVs from conventional is this extra info of oblique contribution.
The next plot offers the SHAP values and CSVs in a motorcycle rental mannequin: taking the cos worth of the time of the 12 months and temperature as enter, the mannequin predicts the bike lease counts. We are able to see that the cos_year worth is attributed to extra significance by CSVs in contemplating the impact of the time of a 12 months on the temperature.

To finish this part, allow us to resume that the Informal SHAP values might be thought to be a generalization of the present SHAP values by changing the marginal expectation of the mannequin with the interventional expectation in order that the oblique contribution of a characteristic is taken into consideration together with its direct contribution.
Allow us to illustrate how CSVs works by contemplating the next easy mannequin with solely three variables:

Allow us to suppose that the variables observe the informal mannequin given by the next DAG through which we suppose that x_1 is the mum or dad of x_2 and x_3 is unbiased of the 2 others.

Furthermore, we suppose that:

Initially, it’s straightforward to get the SHAP values of all options:
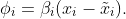
Allow us to transfer to CSVs now. Take the primary characteristic for instance. In line with the definition, a CSVs is given because the sum of the interventional expectation all of permutations of {1,2,3}. For instance, we are going to compute Φ_1(1,2,3). Plugging the linear perform into the definition of Φ, we get:

In line with the informal mannequin, we now have the truth that E[X_2|do(x_1)]=α_1x_1 whereas E[X_3|do(x_1)]=E[X_3] and this results in:

Comparable computation offers the CSVs of all three options:

We observe from the outcomes that CSVs find yourself with completely different characteristic attributions when the mannequin has a sure informal construction. Since X_1 is the mum or dad node of X_2 within the DAG plot proven above, there may be yet one more time period added to the SHAP worth of x_1 as its oblique impact whereas we take away a time period from that of x_2 as it’s attributable to x_1 as an alternative of by x_2 itself.
We wish to say ultimately that whether it is too early to switch SHAP with CSVs. Regardless of the sensible design, CSVs’ limitation is apparent as properly. Basically, we, information scientists are enthusiastic about SHAP for its potential to interpret any black field mannequin whose informal construction could be exhausting to acquire in apply and we’d by no means have an excellent estimation of the do-calculus with the absence of such info. Nonetheless, it will nonetheless assist to get a greater understanding of the mannequin even when solely part of the informal info is offered.


