A simplified clarification and implementation of Rank Biased Overlap
Think about you and your good friend have each watched all 8 Harry Potter films.
However there’s a catch — you’ve got watched every film the day it was launched, with out lacking a single premier.
Your good friend, nonetheless, watched the 2nd film first, then the 4th and fifth, after which binge-watched the remaining when it was out there on Netflix.
Theoretically, you and your good friend are on an equal footing — each have watched all the films of the collection.
Is it actually equal although?
You being a real fan, can by no means take into account it equal.
How may somebody not watch the films of a e book collection, In. A. Sequence?!
You take into account it a sacrilege!
The excellent news is — the maths is in your facet. You’ll be able to boil this drawback down right into a ranked listing comparability.
There are a number of strategies to check lists.
On this submit, you’ll:
- Perceive why we really need a ranked listing comparability
- See the necessities a comparability measure ought to fulfill
- Get an summary of a technique referred to as Rank Biased Overlap
- Perceive the mathematical strategy behind it
- Create a easy implementation in python
On the finish of it, you’ll lastly settle the disagreement together with your good friend as soon as and for all:
You != Your Pal
Aside from the above film viewing order disagreement, we’re surrounded by examples of evaluating lists!
In truth, all of us do such comparisons on a regular basis.
- Which ends are higher for a similar question on Google vs. Bing?
- How related is the New York Occasions bestseller listing to that from USA At the moment?
- How totally different are the highest 10 film rankings on Rotten Tomatoes as in comparison with IMDB?
Within the area of pure language processing and machine studying:
- How related are two paragraphs as soon as they’re transformed to tokenized phrase lists?
- How one can evaluate the ranked outputs generated by two totally different learning-to-rank / machine-learned rating (MLR)¹ fashions?
In manufacturing/manufacturing and logistics:
- Evaluating the sequence of incoming components to the outgoing components (FIFO). A really perfect FIFO sequence appears just like the one under. A 1 goes in first and a 1 comes out first.
However this will not at all times occur in the true world. Perhaps a 1 goes in first however a 3 comes out first?
Yeah, whole chaos can ensue as a result of this.
Then, how are you imagined to measure the standard of the sequences?
You want some sort of measure.
Are there any necessities such a measure should fulfill?
Ideally, a comparability measure must be within the type of a rating that signifies how related the rankings are.
Consider the above examples once more.
You’ll be able to already get clues about what such a measure ought to inform us:
- The ranked lists could also be indefinite and presumably of various lengths — therefore the measure ought to be capable to deal with two totally different listing sizes
- There must be a capability to check at a selected intersecting size — which implies the measure ought to deal with the intersection size of the lists
- The highest components have extra significance (like in search outcomes, film order, and so forth.) than the underside ones — therefore there must be a chance to offer weights at any time when wanted
Now let’s go take a look at one thing that satisfies these situations.
Because the title itself implies, this methodology is rank-biased.
It means you’ll be able to prioritize the highest few components within the listing with a better weight.
It was proposed in a paper titled — A Similarity Measure for Infinite Rankings, by W. Weber et al²
You don’t should undergo the complete complexities within the analysis paper, I simplify many of the components under so we will attempt a fast implementation in Python.
Nevertheless, fasten your seatbelts and put in your math glasses, as we navigate by a couple of labyrinthine formulae!
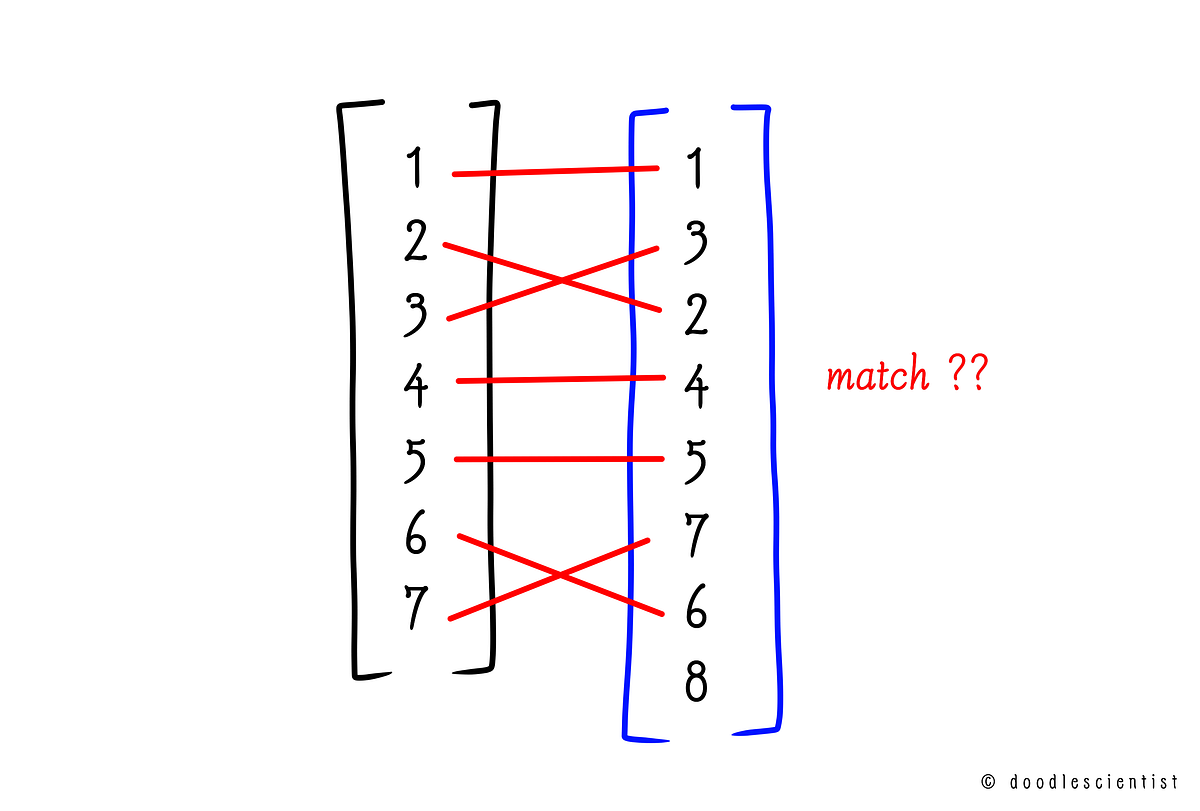
Contemplate S and T because the names of the two ranked lists from our title picture:
Let’s now outline the intersection of those two lists, at a depth (d).
What does this really imply?
It’s the listing of frequent components from S and T, at a given size (referred to as depth d). It is going to be clear from this:
The depth is taken as at most the size of the smaller listing, in any other case, the intersection doesn’t make sense.
The size of this new intersecting listing is known as the Overlap, which on this case is 7.
Subsequent, we outline one thing referred to as the Settlement of the lists. It’s merely the overlap by the depth.
The Common Overlap (AO) is the typical settlement for all of the depths of the lists, starting from 1 to an integer okay.
When okay = 1, the depth ranges from 1 to 1, which implies evaluating solely the primary factor.
For the reason that components match, the intersection X is 1 and so is Settlement A.
Let’s take a look at okay = 2.
On this case, d ranges from 1 to 2, that’s we evaluate the primary 2 components from the lists. The overlap, on this case, is 1 as solely the primary factor is frequent. Therefore, the Settlement is 1/2 or 0.5.
Equally, we will proceed for okay = 3.
Properly, now that you just perceive the way it works, you’ll be able to proceed the method till okay = 7.
You’re going to get the Common Overlap (AO) as:
This could work for any variety of components within the two lists.
We are able to generalize the above summation as:
That is the muse for the similarity measures.
The Common Overlap is a similarity measure, evaluating the 2 lists at a given depth.
Take a household of such similarity measures (SIM):
It’s a geometric collection the place the d’th time period is of type 1/(1-p) the place 0 < p < 1.
Plugging this within the components above and rearranging the phrases, we will get the Rank Based mostly Overlap for the lists S and T as:
The variable p lies within the vary (0, 1) and can be utilized to find out the affect of the primary d components on the ultimate similarity rating.
To get a single RBO rating, the above components might be extrapolated. Assuming that the Settlement until the depth okay is sustained indefinitely among the many two lists, it may be generalized as:
The RBO rating lies between 0 and 1.
- 0 means fully disjoint and 1 means precisely the identical ranked lists.
We’ll use this components for the python implementation of an RBO perform!
The paper additionally exhibits how we will select p for giving a weightage (Wrbo) to the highest d components beneath comparability (I can’t get into the derivation right here):
We’ll use this components to implement the burden calculator perform.
Phew, that was loads to course of!
However don’t fear, the formulae look much more difficult than they really are — you will note how easy it’s with python.
So I hope you might be nonetheless right here as a result of the enjoyable half begins now!
I exploit the above formulae to write down a easy implementation of the Rank Biased Overlap and a weightage calculator perform in python.
Now that you just perceive how RBO is derived, it’s simple to implement.
import mathdef rbo(S,T, p= 0.9):
""" Takes two lists S and T of any lengths and offers out the RBO Rating
Parameters
----------
S, T : Lists (str, integers)
p : Weight parameter, giving the affect of the primary d
components on the ultimate rating. p<0<1. Default 0.9 give the highest 10
components 86% of the contribution within the closing rating.
Returns
-------
Float of RBO rating
"""
# Mounted Phrases
okay = max(len(S), len(T))
x_k = len(set(S).intersection(set(T)))
summation_term = 0
# Loop for summation
# okay+1 for the loop to achieve the final factor (at okay) within the larger listing
for d in vary (1, okay+1):
# Create units from the lists
set1 = set(S[:d]) if d < len(S) else set(S)
set2 = set(T[:d]) if d < len(T) else set(T)
# Intersection at depth d
x_d = len(set1.intersection(set2))
# Settlement at depth d
a_d = x_d/d
# Summation
summation_term = summation_term + math.pow(p, d) * a_d
# Rank Biased Overlap - extrapolated
rbo_ext = (x_k/okay) * math.pow(p, okay) + ((1-p)/p * summation_term)
return rbo_ext
Let’s verify on our instance lists S and T.
S = [1,2,3,4,5,6,7]
T = [1,3,2,4,5,7,6,8]print (rbo(S,T))
>> 0.8853713875
The RBO rating of 0.88 signifies that the lists are almost 90% related (which we noticed additionally within the common overlap calculation earlier than).
That is by no means a strong python implementation.
Nevertheless, it’s clearly adequate to get began!
Now let’s additionally implement the burden calculator perform to assist us select p.
import numpy as np
import mathdef weightage_calculator(p,d):
""" Takes values of p and d
----------
p : Weight parameter, giving the affect of the primary d
components on the ultimate rating. p<0<1.
d : depth at which the burden needs to be calculated
Returns
-------
Float of Weightage Wrbo at depth d
"""
summation_term = 0
for i in vary (1, d): # taking d right here will loop upto the worth d-1
summation_term = summation_term + math.pow(p,i)/i
Wrbo_1_d = 1 - math.pow(p, d-1) +
(((1-p)/p) * d *(np.log(1/(1-p)) - summation_term))
return Wrbo_1_d
Let’s verify if it really works.
As per the analysis paper, p of 0.9 provides the highest 10 components a weightage of 86% within the closing similarity score¹.
Utilizing our above perform:
weightage_calculator(0.9,10)>> 0.8555854467473518
Yay, it really works effectively — it provides 86% as indicated within the paper!
We now have our arsenal prepared.
Let’s settle the rating between you and your good friend!
Let’s check it out by creating lists of Harry Potter films within the order of the way you and your good friend watched them.
After which run your RBO perform on it!
you = ['''Harry Potter and the Philosopher's Stone''',
'Harry Potter and the Chamber of Secrets',
'Harry Potter and the Prisoner of Azkaban',
'Harry Potter and the Goblet of Fire',
'Harry Potter and the Order of Phoenix',
'Harry Potter and the Half Blood Prince',
'Harry Potter and the Deathly Hallows - Part_1'
'Harry Potter and the Deathly Hallows - Part_2']your_friend = ['Harry Potter and the Chamber of Secrets',
'Harry Potter and the Goblet of Fire',
'Harry Potter and the Order of Phoenix',
'''Harry Potter and the Philosopher's Stone''',
'Harry Potter and the Prisoner of Azkaban',
'Harry Potter and the Half Blood Prince',
'Harry Potter and the Deathly Hallows - Part_1'
'Harry Potter and the Deathly Hallows - Part_2']
rbo (you, your_friend)
>> 0.782775
0.78!
So, watching the films out of sequence is certainly totally different, else the rating could be 1!
However you’ll be able to go even additional.
Normally, the primary few films introduce the characters and construct the fictional world — therefore it’s qualitatively extra essential that you just watch them first and within the appropriate order.
Let’s use the burden calculator and provides the primary 4 films extra weightage (86%).
With some trials within the weight calculator perform, we get a weight of 86% for p = 0.75 and d = 4.
weightage_calculator(0.75,4)>> 0.8555854467473518
Therefore, utilizing p as 0.75 within the RBO perform will give the primary 4 films extra affect within the rating comparability:
rbo (you, your_friend, 0.75)
>> 0.5361328125
The ensuing comparability rating is 0.53!
This implies in case you skip the primary few films, or watch them out of sequence, it’s objectively dangerous.
In truth, your good friend’s viewing order is simply half pretty much as good (53%) as in comparison with yours!
And now you’ve got the maths to show it!
Rank-biased overlap shouldn’t be the one methodology for evaluating lists — the opposite strategies are:
- Kendall Tau³
- Pearson’s Correlation⁴
Nevertheless, RBO has a number of benefits over them:
- RBO is appropriate for various lengths of the comparability lists (disjoint or nonsimilar)
- It has a weight measure — you can provide extra significance to the highest or the underside of the comparability
Resulting from these advantages, I made a decision to clarify RBO intimately on this submit.
Nevertheless, be at liberty to take a look at the opposite two as I linked within the sources — they’re additionally utilized in totally different conditions!
To summarize, on this submit you realized one of many measures for evaluating ranked lists — the Rank Biased Overlap.
- You ventured by the arithmetic of it
- Did a easy implementation in python
- Used the features to do a sensible comparability of the film viewing order
- Understood its advantages!
Now anytime there’s a disagreement about evaluating film rankings, viewing order, or principally any sequences, you’ll be able to settle it like a professional!