Most synthetic intelligence at the moment is applied utilizing some type of neural community. In my final two articles, I launched neural networks and confirmed you how one can construct a neural community in Java. The facility of a neural community derives largely from its capability for deep studying, and that capability is constructed on the idea and execution of backpropagation with gradient descent. I will conclude this quick collection of articles with a fast dive into backpropagation and gradient descent in Java.
Backpropagation in machine studying
It’s been mentioned that AI isn’t all that clever, that it’s largely simply backpropagation. So, what is that this keystone of contemporary machine studying?
To know backpropagation, you should first perceive how a neural community works. Principally, a neural community is a directed graph of nodes known as neurons. Neurons have a particular construction that takes inputs, multiplies them with weights, provides a bias worth, and runs all that via an activation operate. Neurons feed their output into different neurons till the output neurons are reached. The output neurons produce the output of the community. (See Types of machine studying: Intro to neural networks for a extra full introduction.)
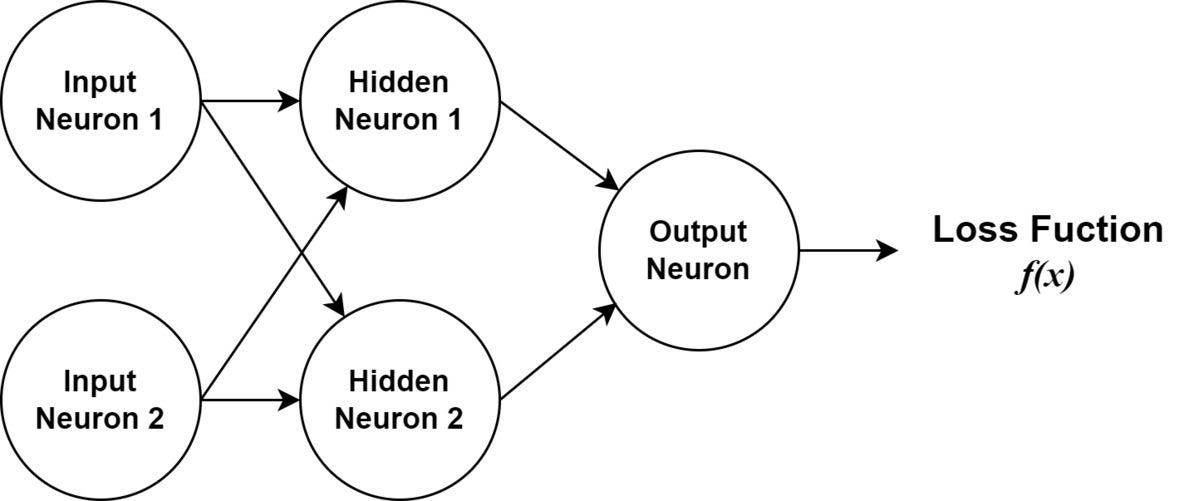
I will assume from right here that you just perceive how a community and its neurons are structured, together with feedforward. The instance and dialogue will concentrate on backpropagation with gradient descent. Our neural community could have a single output node, two “hidden” nodes, and two enter nodes. Utilizing a comparatively easy instance will make it simpler to see the mathematics concerned with the algorithm. Determine 1 reveals a diagram of the instance neural community.
 IDG
IDGDetermine 1. A diagram of the neural community we’ll use for our instance.
The thought in backpropagation with gradient descent is to think about your entire community as a multivariate operate that gives enter to a loss operate. The loss operate calculates a quantity representing how properly the community is performing by evaluating the community output in opposition to recognized good outcomes. The set of enter information paired with good outcomes is called the coaching set. The loss operate is designed to extend the quantity worth because the community’s habits strikes additional away from right.
Gradient descent algorithms take the loss operate and use partial derivatives to find out what every variable (weights and biases) within the community contributed to the loss worth. It then strikes backward, visiting every variable and adjusting it to lower the loss worth.
The calculus of gradient descent
Understanding gradient descent includes just a few ideas from calculus. The primary is the notion of a by-product. MathsIsFun.com has an incredible introduction to derivatives. Briefly, a by-product offers you the slope (or fee of change) for a operate at a single level. Put one other manner, the by-product of a operate offers us the speed of change on the given enter. (The great thing about calculus is that it lets us discover the change with out one other level of reference—or somewhat, it permits us to imagine an infinitesimally small change to the enter.)
The following essential notion is the partial by-product. A partial by-product lets us take a multidimensional (often known as a multivariable) operate and isolate simply one of many variables to seek out the slope for the given dimension.
Derivatives reply the query: What’s the fee of change (or slope) of a operate at a particular level? Partial derivatives reply the query: Given a number of enter variables to the equation, what’s the fee of change for simply this one variable?
Gradient descent makes use of these concepts to go to every variable in an equation and modify it to reduce the output of the equation. That’s precisely what we would like in coaching our community. If we consider the loss operate as being plotted on the graph, we need to transfer in increments towards the minimal of a operate. That’s, we need to discover the worldwide minimal.
Word that the dimensions of an increment is called the “studying fee” in machine studying.
Gradient descent in code
We’re going to stay near the code as we discover the arithmetic of backpropagation with gradient descent. When the mathematics will get too summary, trying on the code will assist hold us grounded. Let’s begin by taking a look at our Neuron class, proven in Itemizing 1.
Itemizing 1. A Neuron class
class Neuron {
Random random = new Random();
non-public Double bias = random.nextGaussian();
non-public Double weight1 = random.nextGaussian();
non-public Double weight2 = random.nextGaussian();
public double compute(double input1, double input2){
return Util.sigmoid(this.getSum(input1, input2));
}
public Double getWeight1() { return this.weight1; }
public Double getWeight2() { return this.weight2; }
public Double getSum(double input1, double input2){ return (this.weight1 * input1) + (this.weight2 * input2) + this.bias; }
public Double getDerivedOutput(double input1, double input2){ return Util.sigmoidDeriv(this.getSum(input1, input2)); }
public void modify(Double w1, Double w2, Double b){
this.weight1 -= w1; this.weight2 -= w2; this.bias -= b;
}
}
The Neuron class has solely three Double members: weight1, weight2, and bias. It additionally has just a few strategies. The tactic used for feedforward is compute(). It accepts two inputs and performs the job of the neuron: multiply every by the suitable weight, add within the bias, and run it via a sigmoid operate.
Earlier than we transfer on, let’s revisit the idea of the sigmoid activation, which I additionally mentioned in my introduction to neural networks. Itemizing 2 reveals a Java-based sigmoid activation operate.
Itemizing 2. Util.sigmoid()
public static double sigmoid(double in){
return 1 / (1 + Math.exp(-in));
}
The sigmoid operate takes the enter and raises Euler’s quantity (Math.exp) to its adverse, including 1 and dividing that by 1. The impact is to compress the output between 0 and 1, with bigger and smaller numbers approaching the boundaries asymptotically.
Returning to the Neuron class in Itemizing 1, past the compute() technique we’ve got getSum() and getDerivedOutput(). getSum() simply does the weights * inputs + bias calculation. Discover that compute() takes getSum() and runs it via sigmoid(). The getDerivedOutput() technique runs getSum() via a special operate: the by-product of the sigmoid operate.
By-product in motion
Now check out Itemizing 3, which reveals a sigmoid by-product operate in Java. We’ve talked about derivatives conceptually, here is one in motion.
Itemizing 3. Sigmoid by-product
public static double sigmoidDeriv(double in){
double sigmoid = Util.sigmoid(in);
return sigmoid * (1 - sigmoid);
}
Remembering {that a} by-product tells us what the change of a operate is for a single level in its graph, we are able to get a really feel for what this by-product is saying: Inform me the speed of change to the sigmoid operate for the given enter. You may say it tells us what influence the preactivated neuron from Itemizing 1 has on the ultimate, activated consequence.
By-product guidelines
You would possibly marvel how we all know the sigmoid by-product operate in Itemizing 3 is right. The reply is that we’ll know the by-product operate is right if it has been verified by others and if we all know the correctly differentiated capabilities are correct primarily based on particular guidelines. We don’t have to return to first rules and rediscover these guidelines as soon as we perceive what they’re saying and belief that they’re correct—very similar to we settle for and apply the foundations for simplifying algebraic equations.
So, in apply, we discover derivatives by following the by-product guidelines. When you take a look at the sigmoid operate and its by-product, you’ll see the latter might be arrived at by following these guidelines. For the needs of gradient descent, we have to find out about by-product guidelines, belief that they work, and perceive how they apply. We’ll use them to seek out the function every of the weights and biases performs within the remaining loss consequence of the community.
Notation
The notation f prime f’(x) is a technique of claiming “the by-product of f of x”. One other is:
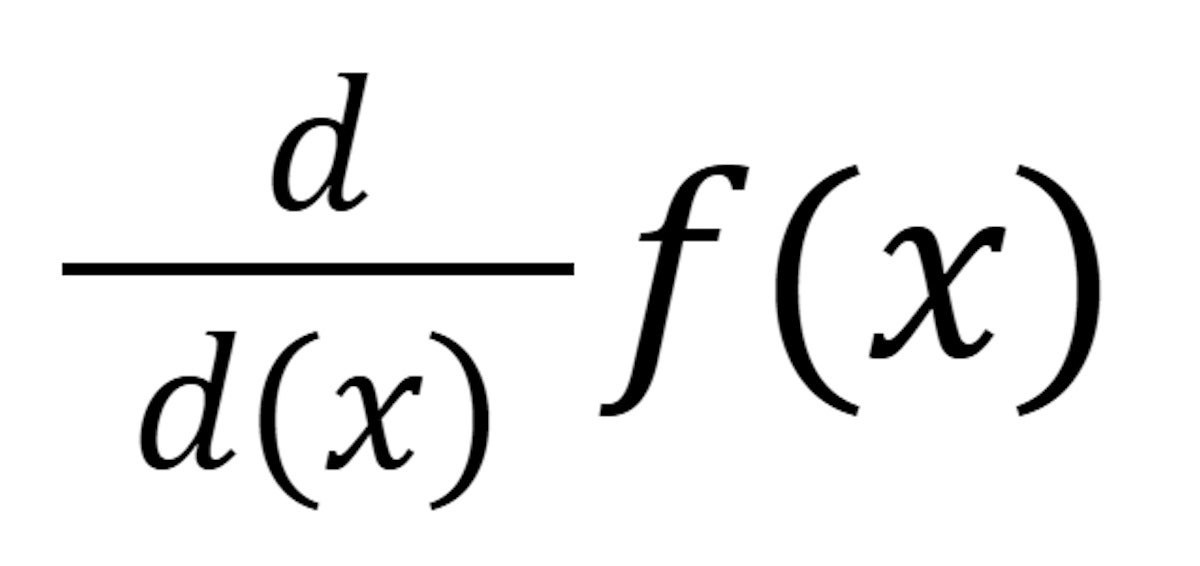 IDG
IDGThe 2 are equal:
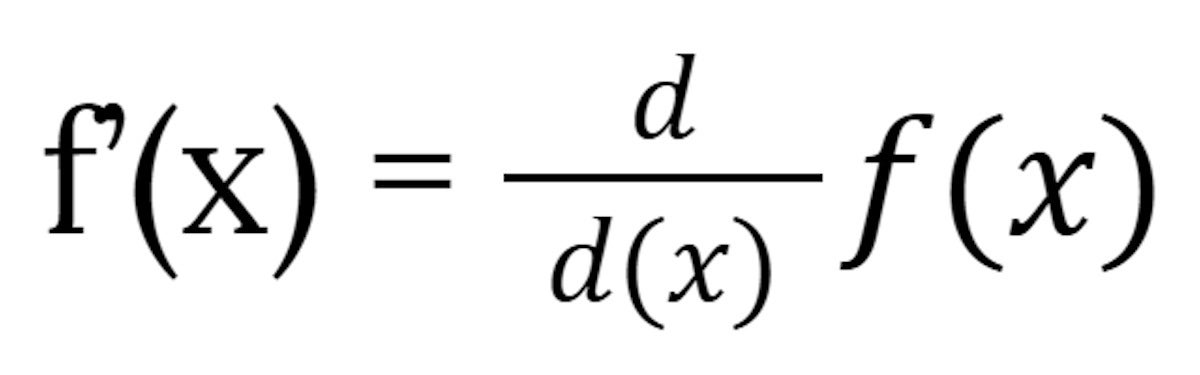 IDG
IDGOne other notation you’ll see shortly is the partial by-product notation:
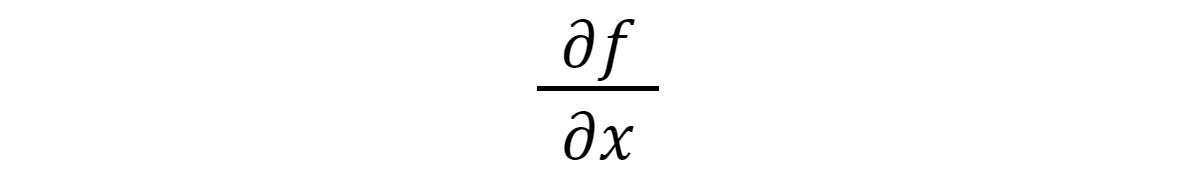 IDG
IDGThis says, give me the by-product of f for the variable x.
The chain rule
Essentially the most curious of the by-product guidelines is the chain rule. It says that when a operate is compound (a operate inside a operate, aka a higher-order operate) you’ll be able to broaden it like so:
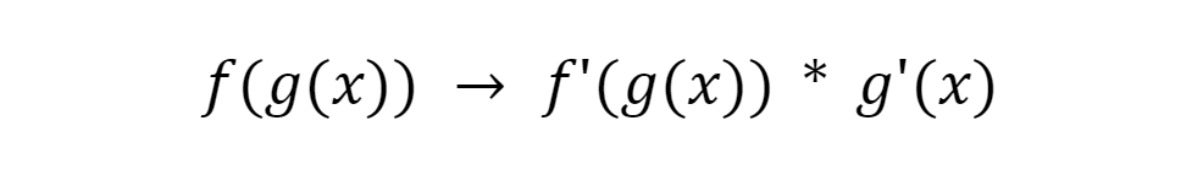 IDG
IDGWe’ll use the chain rule to unpack our community and get partial derivatives for every weight and bias.


