
Puzzles, mixtures and answer gifs.
On this put up, a strategy to resolve Nonograms with none errors is proven by calculating the choices for each line. It’s not essentially the most environment friendly strategy to come to an answer, in the long run you could find extra details about the quickest method. In my view, that is essentially the most enjoyable method as a result of it leaves no room for errors. And as a bonus, you’ll study a bit extra about counting issues! Let’s leap in!
A Nonogram (aka Griddler, Paint By Numbers, Hanjie or Picross) is a puzzle during which you attempt to reveal an image. It’s a logic puzzle with easy guidelines. You have got a grid with squares, and each sq. ought to grow to be black or white. Numbers on the facet and prime of the grid reveal the teams of black squares that ought to be in each row and column.
Fixing Course of
Let’s begin with an empty Nonogram:
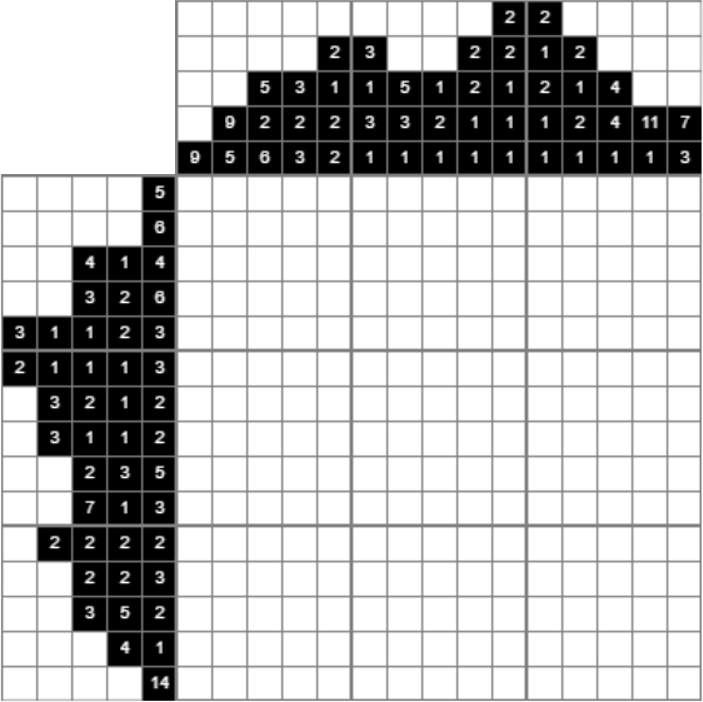
The third column has the values 5, 2 and 6. This means there are units of 5, two, and 6 stuffed squares, in that order, with no less than one clean sq. between successive units. As a result of 5 + 1 (white sq.) + 2 + 1 (white sq.)+ 6 is the same as 15, this line is simple to unravel, there is just one doable answer:

The dots are serving to marks to point that these squares ought to be empty.
Let’s proceed. The bottom line comprises a gaggle of 14 black squares, and since the entire line is 15 squares lengthy, we are able to fill all squares in addition to the primary and the final one:

We are able to use these stuffed squares, as a result of they correspond with the column values on the underside:

Received it? Through the use of some logic it’s fairly simple to unravel this Nonogram! You’ll be able to do that one by your self or proceed studying and let the pc resolve it for you.
Spoiler alert: a gif will present the fixing means of this Nonogram on the finish.
After understanding the foundations of the sport, how can we let the pc resolve Nonograms utilizing math?
This system consists of three steps. Step one solely occurs originally and is essentially the most difficult one, whereas step 2 and step 3 are simple to grasp and shall be repeated till the puzzle is solved.
Step 1. Calculate all choices for each row and column
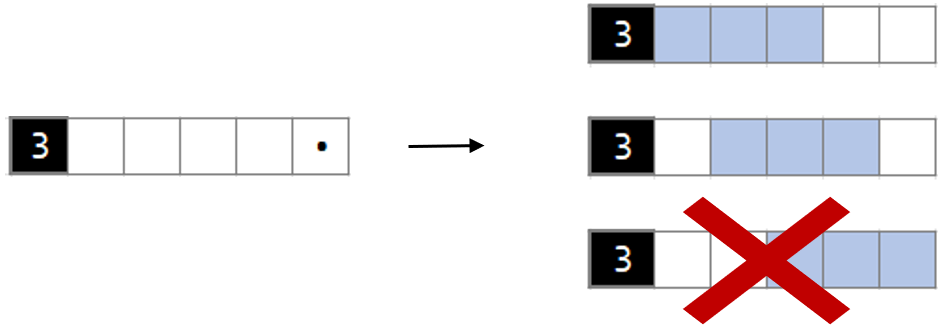
We begin by calculating all choices to pick out black squares for each row and column (the following part explains how to do that if issues get extra difficult). This solely occurs originally of the sport. Let’s say we’ve got a row of 5 squares and we wish to fill it with one group of three:

This provides us the three choices on the suitable.
Step 2. Fill squares which have just one chance
When you have a look at the choices for one row and also you uncover that there’s just one chance for a sure sq., as a result of in all choices the sq. is black or in all choices the sq. is white, the sq. can solely be stuffed with this colour. This instance illustrates this:

Step 3. Take away choices from the corresponding row or column
After filling a sq. (or making it white), we are able to have a look at the corresponding row or column and take away all choices during which this sq. is the opposite colour. As a result of these choices aren’t doable anymore. Instance:
The way to calculate all choices for each row and column?
The calculation of choices was simple within the instance above, we slide the group of three to the left till we attain the tip of the row. However what occurs if we take a extra difficult checklist with values and attempt to discover all doable choices? One other instance:

Within the instance above we place the teams 3, 2 and 6 in a row with 15 squares. We want no less than 13 squares for this mixture of teams:
6 + 1 white sq. + 3 + 1 white sq. + 2 = 13
This implies we’ve got 2 empty squares left (15 minus 13 = 2).
An attention-grabbing factor to note is that for the variety of whole choices you solely must know the variety of empty squares left and the variety of teams you bought. An intuitive proof:

Okay, we’re making progress! On this instance we see that if we acquired three teams with values (6, 2, 3 on the left and 1, 1, 1 on the suitable), and two empty squares left, the entire variety of doable choices is 10.
If we overlook concerning the white squares between teams (these ought to be there it doesn’t matter what), we are able to calculate the variety of choices utilizing mixtures. We acquired 5 locations (3 teams + 2 empty squares) and wish to pick out 3 out of 5 (we wish to place 3 teams). Right here you could find a bit extra about mixtures. It’s simple to calculate all mixtures utilizing python and itertools.
from itertools import mixturesopts = mixtures(vary(n_groups+n_empty), n_groups)

This additionally works for the three, 2, 6 values, besides we now place extra ones on the locations:

That’s it! This works for all teams of values. We solely want the variety of empty squares left and the variety of teams to create all doable choices utilizing mixtures.
There’s no want to unravel a Nonogram by hand after the creation of this program. Let’s resolve some Nonograms!
Let’s begin with a small one:

Can it resolve the Nonogram we began with?

Sure, after all!
And the ultimate one, what a couple of actually giant Nonogram?

Works fairly quick too!
Wish to resolve Nonograms utilizing this program? Beneath you could find a gist with python code. You solely must specify the row values as a listing of lists and the column values as a listing of lists. When you name the NonogramSolver class it can begin fixing your Nonogram. You’ll be able to select to avoid wasting all of the steps by specifying the savepath variable.
The Nonogram solver we created has some advantages: it can by no means fill a sq. it’s not utterly sure about. The draw back of this strategy is computation time. If the puzzles grow to be bigger, extra choices can be found for the rows and columns and the time it takes to unravel the puzzle will grow to be longer. One other draw back is that it will probably’t resolve Nonograms with a number of options.
Fortunately, some folks already solved these issues. So if you’re searching for an excellent quick Nonogram solver that may deal with Nonograms with extra options, you may discover this text attention-grabbing.
Don’t overlook to subscribe in the event you’d wish to get an e-mail at any time when I publish a brand new article.





