Logistic Regression is among the supervised machine studying methods which might be used for classification duties. Classification datasets more often than not may have a category imbalance with a sure class with extra samples and sure lessons with a really much less variety of samples. Utilizing an imbalanced dataset for the mannequin constructing would account for the unsuitable prediction and can be extra favorable to lessons with extra samples. So on this article allow us to attempt to perceive the significance of sophistication weights in logistic regression and why a steadiness of sophistication weights is critical to yield a dependable mannequin.
Desk of Contents
- What are class weights?
- Issues related to imbalanced class weights
- Understanding the significance of sophistication weights
- Steps to computing class weight
- Abstract
What are class weights?
Class weights are terminology used for classification duties the place every class of the dataset can be supplied with sure weights in accordance with the frequency of prevalence of every class. So class weights can be chargeable for giving equal weights for all classes on gradient updates. The utilization of unbalanced class weights can be chargeable for bias in the direction of probably the most occurring classes within the information. To acquire a extra dependable and unbiased classification mannequin you will need to have a uniform distribution of sophistication weights. Uniform distribution of sophistication weights will even yield numerous parameters like precision, recall, and F1 rating as the category weights can be balanced.
Now allow us to attempt to perceive the issues related to an imbalance in school weights.
Are you on the lookout for an entire repository of Python libraries utilized in information science, take a look at right here.
Issues related to imbalanced class weights
The principle drawback related to imbalanced class weights is accuracy. The accuracy produced on this planet is excessive however what issues is the rightness of accuracy. For imbalance class weights the accuracy yielded can be excessive usually as it might be biased in the direction of probably the most occurring class as it might account for larger class weights.
Say suppose healthcare information or business-driven information is in use and there may be an imbalance of sophistication weights. So if the category imbalance within the information is just not addressed it might account for misinterpretations from the mannequin. Furthermore, sure parameters like False-positive and False negatives would transform 0 because the mannequin will be predisposed extra towards the regularly occurring class.
Understanding the significance of sophistication weights
To grasp the significance of sophistication weights allow us to contemplate a classification dataset which is having an imbalance within the goal variable distribution.
Right here a healthcare dataset is getting used and let’s analyze the uneven distribution of the goal variable by a depend plot.
sns.countplot(y)

Right here we will see that the goal variable is vastly imbalanced the place class 0 is having larger class weights when in comparison with class 1. So allow us to construct a logistic regression with the imbalance goal variable and attempt to consider sure parameters from the mannequin.
X=df.drop('stroke',axis=1)
y=df['stroke']
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.2,random_state=42)
from sklearn.linear_model import LogisticRegression
lr_imb=LogisticRegression(random_state=42)
lr_imb_model=lr_imb.match(X_train,Y_train)
y_pred=lr_imb_model.predict(X_test)
print('Classification report of imbalanced logistic regression n',classification_report(Y_test,y_pred))

plot_confusion_matrix(lr_imb_model,X_test,Y_test)

From the classification report, we will observe that the harmonic imply (F1-score) is extra for the category with extra weightage, and for the category with lesser weightage the harmonic imply and different parameters are 0. Furthermore, the mannequin has yielded an accuracy rating of 94% which signifies that the mannequin would make unsuitable predictions and can be extra inclined to the regularly occurring lessons. So that is the main drawback related to imbalanced class weights and it seems to steadiness the category weights to yield an unbiased and extra dependable mannequin.
Balancing class weights
The category weights could be balanced utilizing the logistic regression mannequin by simply declaring the class_weight parameter as balanced within the logistic regression mannequin. The category weights could be balanced robotically bypassing the usual parameter as balanced in school weights or random weights to every of the lessons could be offered to every of the classes within the information.
Now allow us to look into steadiness the weights utilizing the predefined “balanced parameter” of the scikit study library.
Utilizing the “balanced” parameter for sophistication weights
Now the logistic regression mannequin is being fitted with class weights as a typical parameter as “balanced”. The parameter is quickly made accessible in scikit-learn fashions. Allow us to see use this parameter and procure a logistic regression mannequin and consider sure parameters.
lr_bal=LogisticRegression(random_state=42,class_weight="balanced")
lr_bal_model=lr_bal.match(X_train,Y_train)
y_pred_bal=lr_bal_model.predict(X_test)
print('Classification report for balanced lessons n',classification_report(Y_test,y_pred_bal))

plot_confusion_matrix(lr_bal_model,X_test,Y_test)
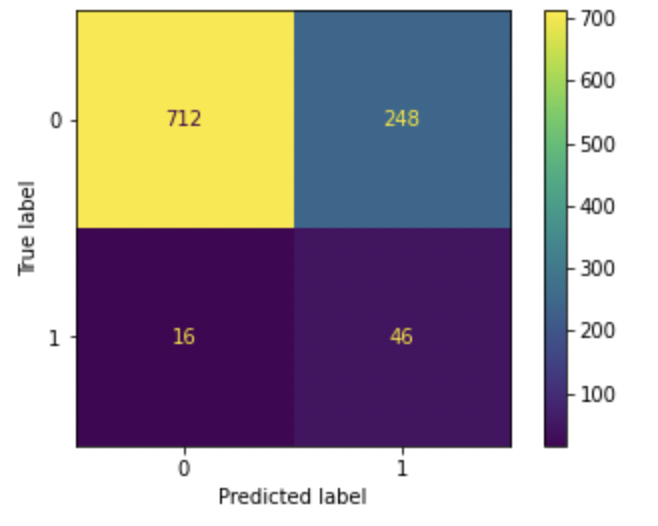
Right here we will see that after utilizing the category weights as balanced whereas becoming the logistic regression mannequin we will see that the accuracy has decreased when in comparison with the imbalance mannequin however the harmonic imply for the decrease occurring class has seen a rise. Different parameters like precision, recall, and F1-score have additionally seen a rise which helps machine studying engineers to suitably make interpretations from the mannequin.
This mannequin could be additional hyper tuned to yield even higher parameters and efficiency. Furthermore, if the confusion matrix can be evaluated we will see that we’re capable of yield the correct parameters like False optimistic and false unfavorable which reveals that the mannequin is just not inclined or biased in the direction of the regularly occurring class.
Balancing class weights utilizing the dictionary as a parameter
Class weights can be balanced utilizing a dictionary the place the dictionary keys are the lessons of the dataset and the keys of the dictionary can be the share of weights that may be assigned to every of the lessons of the info. So allow us to look into use a dictionary as a parameter for sophistication weights and consider sure parameters of the mannequin.
lr_bal2=LogisticRegression(random_state=42,class_weight={0: 0.2,1: 0.8}).match(X_train,Y_train)
y_pred_bal2=lr_bal2.predict(X_test)
print(classification_report(Y_test,y_pred_bal2))

plot_confusion_matrix(lr_bal2,X_test,Y_test)

So after utilizing a random distribution of weights among the many lessons within the information we’ve seen a rise within the mannequin accuracy when in comparison with utilizing the “balanced” parameter however right here a steadiness of sophistication weights with a share of 80 and 20 is proven. So if the lessons are balanced equally or close to to equal the mannequin will yield efficiency much like the mannequin obtained by utilizing the “balanced” parameter.
So that is how imbalance and steadiness of sophistication weights account for the mannequin efficiency. On the whole, it’s a good apply to make use of balanced information to yield a dependable mannequin and procure the correct predictions from the mannequin. Now allow us to attempt to perceive that class weights are being calculated for various class weight parameters.
Steps to compute the category weights
The category weights for any classification issues could be obtained utilizing commonplace libraries of scikit-learn. However you will need to perceive how scikit-learn internally computes the category weights. The category weights are usually calculated utilizing the system proven beneath.
w(j)=n/Kn(j)
w(j) = weights of the lessons
n = variety of observations
Ok = Whole variety of lessons
n(j) = Variety of observations in every class
So the scikit-learn utils library internally makes use of this system to compute the category weights with totally different units of parameters getting used for sophistication weights. Now allow us to look into use the scikit- study utils library for calculating the category weights at totally different situations.
Calculating imbalance class weights
For calculating the category weights the “compute_class_weight” inbuilt operate is getting used as proven beneath and correspondingly the category weights for minority and majority lessons could be computed as proven beneath.
# Calculate weights utilizing sklearn
sklearn_weights1 = class_weight.compute_class_weight(class_weight=None,y=df['stroke'],lessons=np.distinctive(y)) sklearn_weights1

Right here the weights assigned to each the lessons are equal. Allow us to compute the weights for every of the lessons.
# Evaluate the values
print(f'The weights for almost all class is {sklearn_weights1[0]*2:.3f}')
print(f'The weights for the minority class is {sklearn_weights1[1]*2:.3f}')

Right here we will see that for imbalanced lessons the weights assigned to each minority and majority lessons are the identical which accounts for the bias of the mannequin towards the bulk lessons.
Calculating class weights after utilizing the “balanced” parameter
The category weights could be calculated after utilizing the “balanced” parameter as proven beneath.
sklearn_weights2 = class_weight.compute_class_weight(class_weight="balanced",y=df['stroke'],lessons=np.distinctive(y)) Sklearn_weights2

Right here we will see that extra weightage is given to class 1 because it has a lesser variety of samples when in comparison with class 0. So allow us to attempt to receive the weights which could be simply interpreted as proven beneath.
# Evaluate the values
print(f'The weights for almost all class is {sklearn_weights2[0]*2:.3f}')
print(f'The weights for the minority class is {sklearn_weights2[1]*2:.3f}')

So right here we will see that the “balanced” parameter has offered extra weightage to the minority class when in comparison with the bulk class which helps us to yield a greater dependable mannequin.
Calculating class weights by utilizing the dictionary as a parameter
Right here the category weights can be calculated by offering random percentages of distribution of weights to every class of the info as proven beneath.
# Calculate weights utilizing sklearn
dict1={0: 0.2,1: 0.8}
sklearn_weights3 = class_weight.compute_class_weight(class_weight=dict1,y=df['stroke'],lessons=np.distinctive(y))
sklearn_weights3

Right here we will see that as specified 20% of the weights is utilized to class 0 and 80% of weightage is utilized to class 1 of the dataset. Now allow us to attempt to interpret the category weights as proven beneath for straightforward understanding.
print(f'The weights for almost all class is {sklearn_weights3[0]*2:.3f}')
print(f'The weights for the minority class is {sklearn_weights3[1]*2:.3f}')

So that is how class weights for various lessons within the dataset are enforced by utilizing the weightage that’s offered within the dictionary for every of the lessons.
Abstract
Class weights play an important position in any of the classification machine studying fashions. So on this article, we’ve seen how class weights and the steadiness of sophistication weights are essential to acquire a dependable mannequin. Class weight steadiness may be very important to acquire a bias-free mannequin that may be taken up for the correct predictions. The imbalance of sophistication weights accounts for defective predictions and false interpretations from the mannequin. So it is vitally essential to steadiness the category weights to acquire a dependable mannequin that can be utilized for predictions in real-time.
Reference


