How Okay-Means can be utilized to considerably scale back the file dimension of a picture.
On this information, I describe and implement the k-means algorithm from scratch and apply it to picture compression. I exploit totally different visualizations to assist the reader develop a stronger understanding of the k-means algorithm and the way it may be used for picture compression. I additionally talk about varied benefits and limitations of this strategy in direction of the tip.
All photos except in any other case famous are by the writer, out there right here.
The k-means algorithm is an unsupervised algorithm that partitions a dataset into okay distinct clusters. It’s unsupervised, which means there are not any labels for the info factors. In different phrases, we don’t have prior data of how the dataset needs to be clustered. We merely present the dataset as is, and use k-means to partition it into okay clusters.
Large Image Thought
Okay-means seeks to divide a dataset into okay clusters the place members of every cluster share traits and are totally different from different clusters. Due to this fact, the purpose is for k-means to divide the dataset meaningfully into okay totally different clusters.
Purposes
Cluster evaluation teams related knowledge collectively by abstracting the underlying construction of a dataset, which might present significant perception. “Clustering has been successfully utilized in a wide range of engineering and scientific disciplines comparable to psychology, biology, medication, pc imaginative and prescient, communications, and distant sensing” [1].
The Okay-means algorithm is damaged into a number of steps:
- Initializing a set of cluster centroids
- Assigning observations to clusters
- Updating the clusters
Steps 2 and three are repeated for both a set variety of iterations or till convergence, which happens when the cluster centroids not change.
Allow us to dive deeper into every of those steps.
1. Initializing the set of cluster centroids
Step one to initializing the set of cluster centroids is selecting what number of centroids we wish to use, which we discuss with as okay.
As soon as, we’ve got chosen the variety of clusters, we select okay samples randomly from the coaching examples, and set the cluster centroids to be equal to the values of the chosen okay examples. Alternatively, we will randomly pattern okay totally different factors within the resolution house to initialize the cluster centroids.
We discuss with the j-th centroid as μⱼ, as a result of it represents the imply of the values assigned to cluster j. That is the place the title k-means arises from. Within the determine beneath, we set okay=3 and randomly pattern 3 factors within the pattern house (represented by inexperienced, blue, and pink ‘x’) to initialize the cluster centroids.
2. Assigning Observations to Clusters
Now that we’ve got our okay centroids, we assign every statement (knowledge level) to the centroid closest to it. Sometimes, we calculate “closeness” utilizing the euclidean distance. Within the determine beneath, we illustrate the method of assigning the observations to the three centroids above.
3. Updating the Centroids
As soon as all the observations have been assigned to a cluster, we shift the centroid of every cluster to the imply of its assigned observations. We illustrate this course of beneath.
Repeat until convergence or for a sure variety of iterations
Every iteration of the k-means algorithm consists of two components: Step 2 (Assigning Observations to Clusters) and Step 3 (Updating the Clusters). This course of is repeated for both a set variety of iterations or till convergence. Convergence happens when the cluster centroids not change. That is equal to saying that the assignments of the observations don’t change anymore.
The okay means algorithm will at all times converge inside a finite variety of iterations [2] however it’s vulnerable to native minima [3].
Within the instance beneath, the okay means algorithm converges at iteration 4. It is because the cluster centroids not change after iteration 4.
The purpose of picture compression is to scale back the file dimension of a picture. We are able to use Okay-means to pick out okay colours to characterize a whole picture. This enables us to characterize a picture utilizing solely okay colours, as a substitute of your entire RGB house. This course of can also be known as picture quantization.
Why Okay-means is beneficial for picture compression
The aim of utilizing k-means for picture compression is to pick out okay colours to characterize a goal picture with the least approximation error. In different phrases, we shall be utilizing k-means to search out the finest okay colours to characterize a goal picture with.
How Okay-means supplies compression
The colour pixels in a picture are represented by their RGB values, which every vary from 0 to 255. Since every coloration band has 256=2⁸ settings, there are a complete of 256 ⋅ 256 ⋅ 256 = 256³ = 2²⁴ ~ 17 million colours. To characterize every of those colours for any pixel, computer systems want log₂(2²⁴) = 24 bits of space for storing. If we use Okay-means to pick out 16 colours that we characterize a whole picture with, we solely want log₂(16) = 4 bits. Due to this fact, by utilizing Okay-means with okay=16, we will compress the picture dimension by an element of 6!
Now that we perceive the idea, allow us to dive into some code and visualizations.
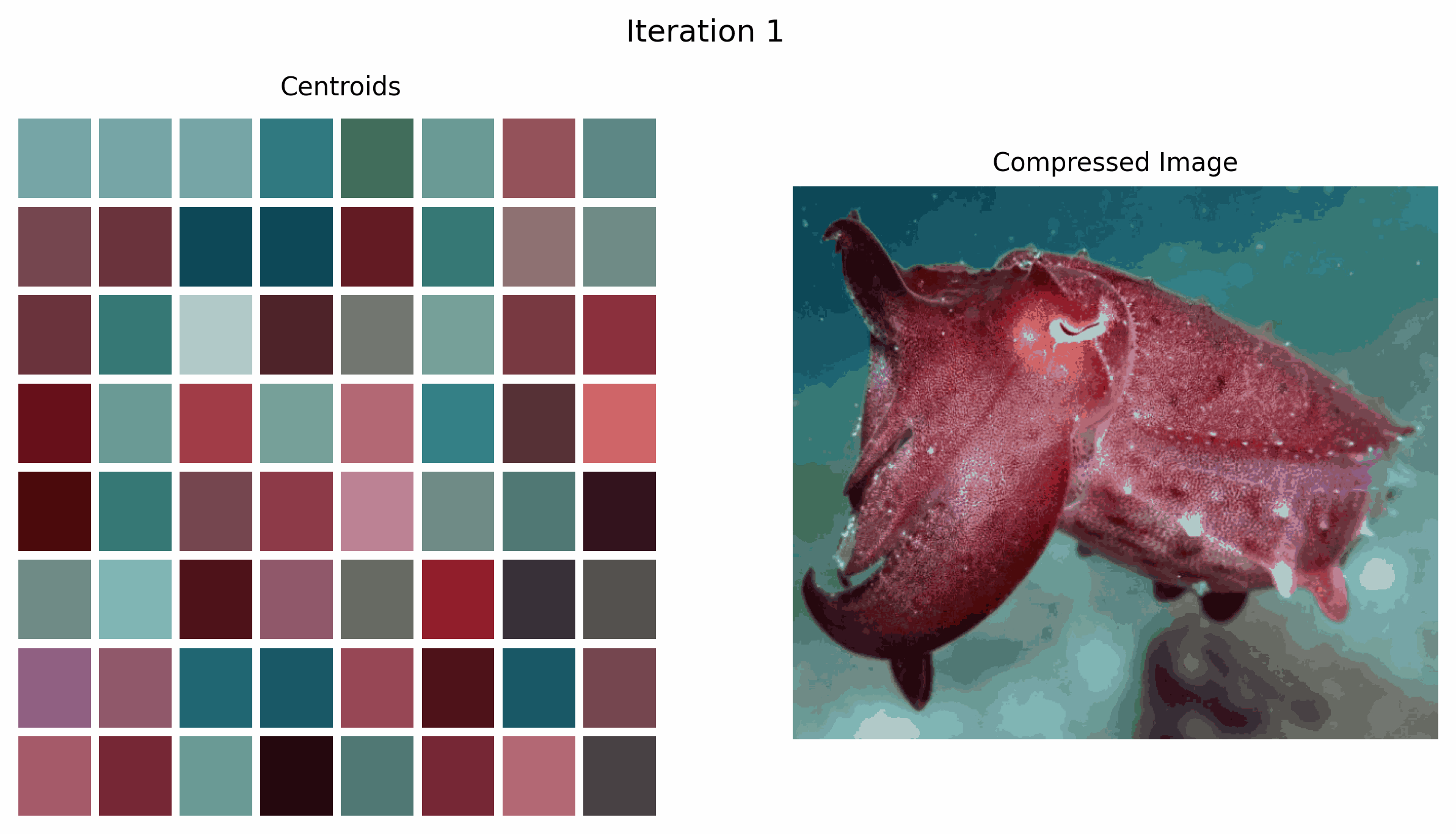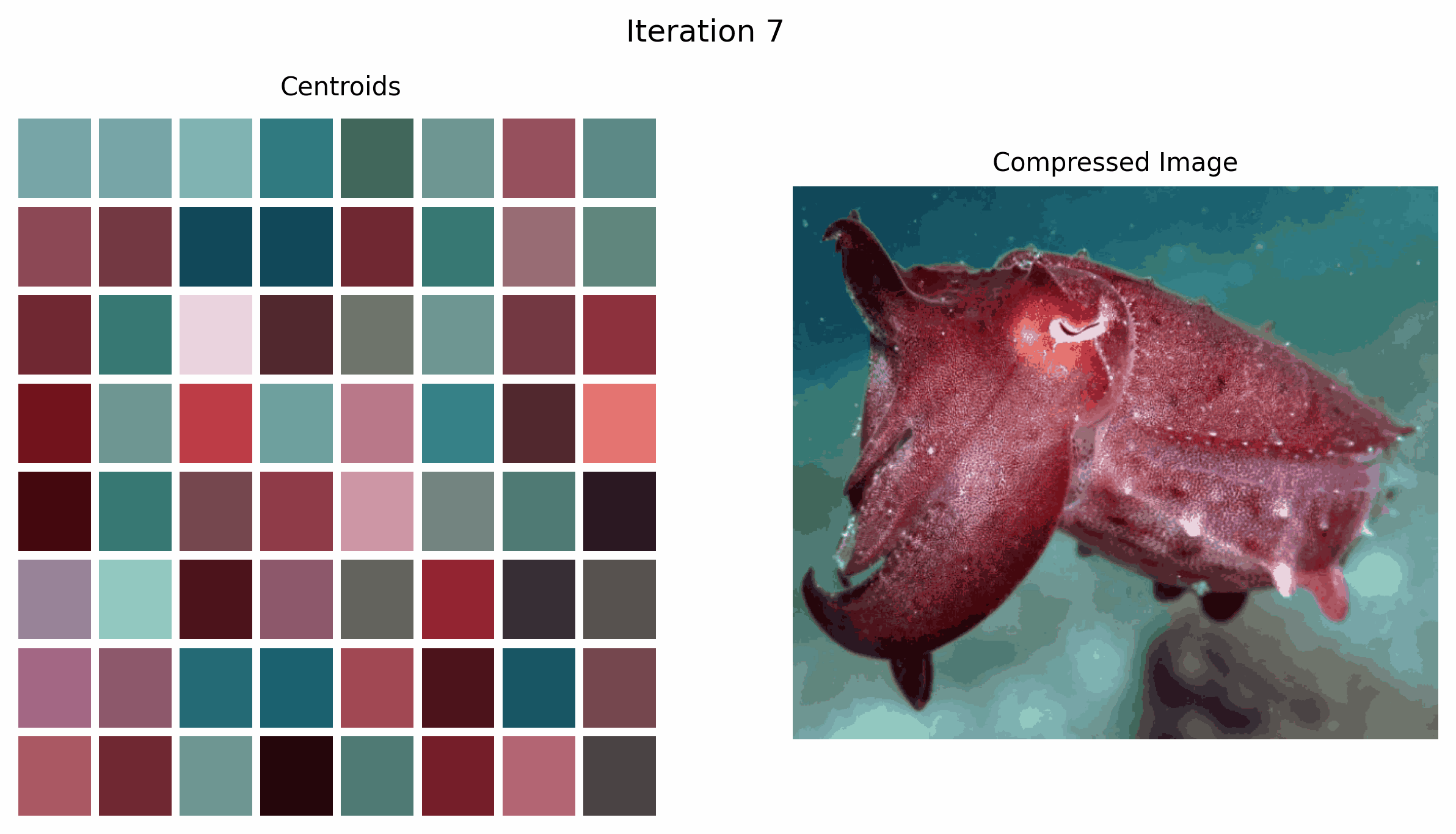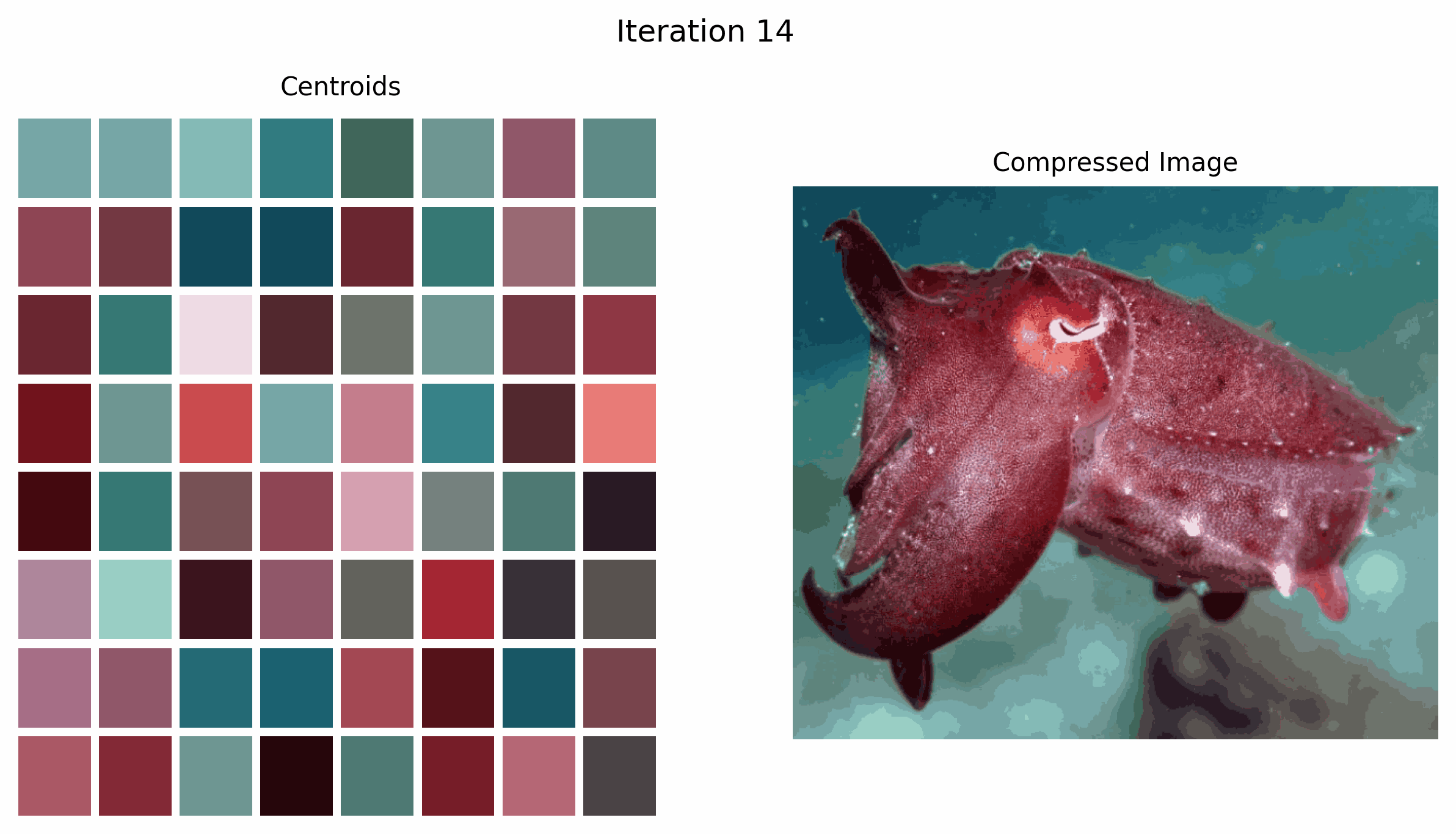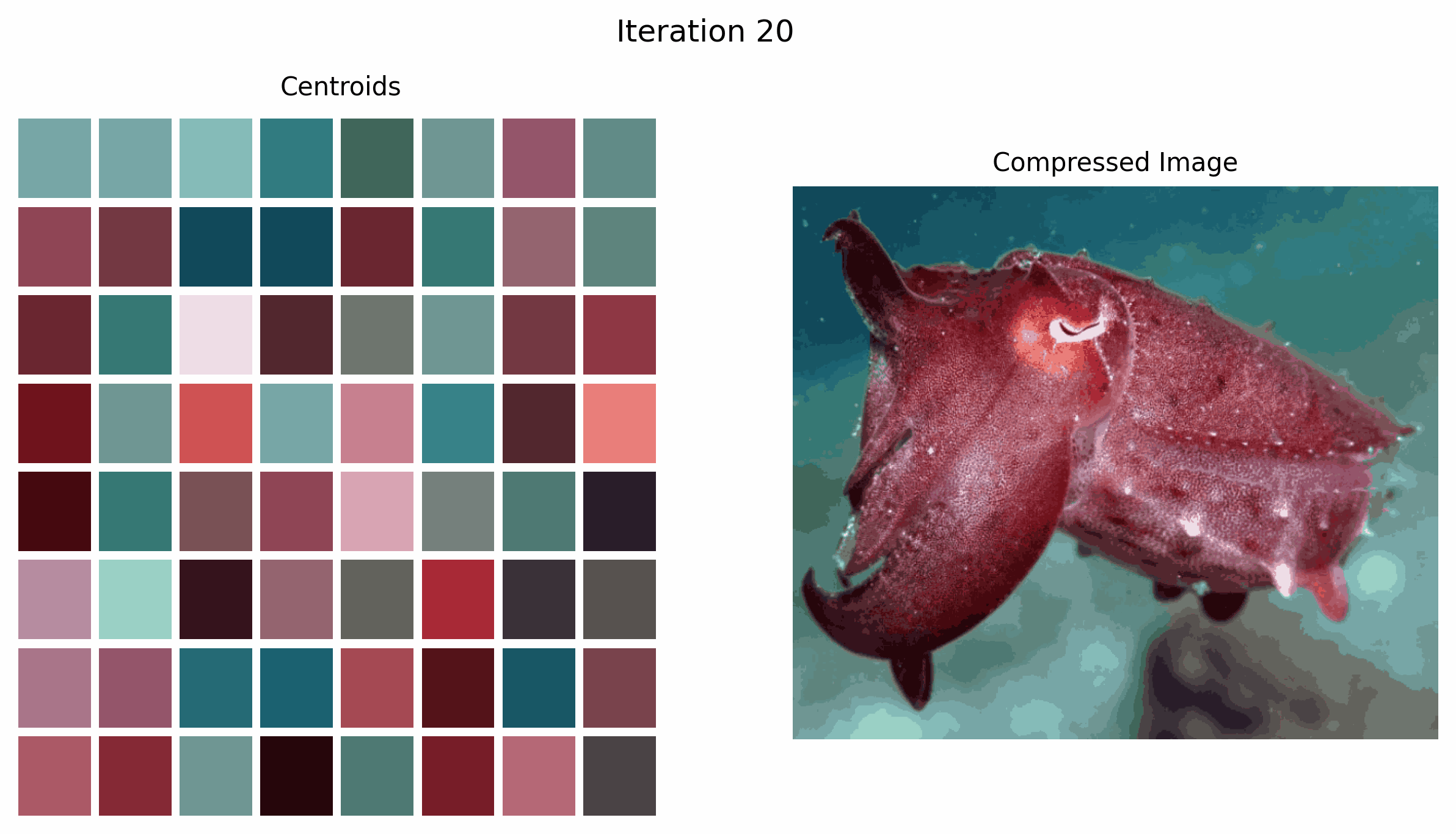
Studying within the Picture and Initializing the Centroids
Within the context of picture compression, the centroids are the colours we’re utilizing to characterize the compressed picture. Due to this fact, our first step is to learn within the picture and choose okay random colours from the picture to initialize our centroids.
In line 7, we learn within the picture utilizing numpy. This produces a 2 dimensional array the place every component is an inventory of size 3 that represents the RGB values of that pixel. Keep in mind to switch image_path to your individual.
Beginning on line 9, we outline the operate to initialize our centroids. We choose a random pixel from the picture and add its corresponding RGB worth to the centroids_init array. We do that okay = num_clusters occasions. Thus, centroids_init is an array of okay colours sampled randomly from our picture.
Assigning and Updating Centroids
To iteratively replace our centroids, we repeat the method of assigning observations to cluster centroids and updating the centroids to be the imply of the assigned observations.
Within the context of picture compression, this implies assigning every pixel of the goal picture to the centroid coloration that’s nearest to it.
In traces 11–17, we’re creating the dictionary centroid_rgbs . Every key corresponds to an index of the centroids and the values are a single numpy array that include all the colours assigned to the corresponding centroid.
The project of every pixel to a centroid is completed on line 13 utilizing linalg.normto calculate the euclidean distance to every centroid after which utilizing argminto search out the index of the closest centroid.
Creating the Compressed Picture
Now that we’ve got the finalized centroids, we will create the compressed picture. We merely iterate via every pixel and alter its coloration to the closest centroid.
Placing Every part Collectively
With the next snippet and the operate definitions above, all of the items to working k-means for picture compression are full.
To generate the GIF’s, I used plt.savefig at varied phases of the algorithm. My github repository accommodates the code for that course of, and methods to convert these frames to a GIF [4].
Within the GIF above, we see how the centroids, that are the colours we select to characterize the picture, change over time because the k-means algorithm iterates.
Now, we analyze some particulars relating to the usage of k-means for picture compression.
Outliers
Usually, photos will include outlier colours relative to the primary coloration palette of the picture. For instance, the goal picture beneath accommodates two small clown-fish which are vivid orange. Their coloration contrasts strongly from the darkish background and sea anemone, which attracts the viewers consideration to them (hopefully in an aesthetically pleasing means).
The GIF beneath illustrates what occurs once we apply k-means to this picture for okay=16. Though the clown-fish’s vivid orange is chosen as an preliminary cluster, it’s finally ‘washed out’ by the darker colours because the algorithm iterates.
Though the general high quality of the compressed picture will increase because the variety of iterations will increase, the accuracy of the outlier coloration decreases.
Some literature suggests creating clusters particularly for outliers (calculated utilizing a distance metric) to enhance general clustering accuracy [5]. The authors’ use of numerical experiments on each artificial knowledge and actual knowledge are supplied to show the effectiveness and effectivity of their proposed algorithm. I think that implementing this algorithm may assist with picture compression utilizing k-means, particularly with photos that include outlier colours.
Choosing “okay”
The selection of okay determines the quantity of compression, and is as much as the consumer to set. The next worth of okay will present for a extra trustworthy illustration of the goal picture, however comes at the price of decrease compression. Within the graphic beneath, we illustrate compressed photos with rising values of okay. The compression elements for okay=16, okay=32, okay=64, and okay=128 are 6, 4.8, 4, and 3.4 respectively.
Within the instance above, we see that selecting a okay worth higher than 32 is crucial in mitigating the outlier subject talked about within the earlier part. Since okay is giant sufficient, at the least one centroid is ready to be assigned to the intense orange coloration. Within the determine beneath, we plot the centroid colours after 30 iterations for each okay=64 and okay=256.
After 30 iterations, okay=64 has one centroid that’s assigned to orange. For okay=256, there are roughly 4 shades of orange.
This visualization additionally portrays the compression quantity vs. element trade-off for various k-values. Clearly for bigger values of okay, we’ve got extra colours and retention of element, nevertheless we require extra knowledge to characterize these colours.
It’s possible value experimenting with totally different values of okay relying on the goal picture and use case.
Lossy Compression
Utilizing the k-means algorithm to compress a picture is a type of lossy compresion. Lossy compression is a category of information compression that makes use of approximations and partial knowledge lack of a goal picture [6]. After we use k-means for picture compression, we’re approximating every pixel’s coloration utilizing the closest centroid. Since we’re shedding info on this course of, we can not revert the compressed picture again to the unique. This is the reason lossy compression can also be refered to as irreversible compression.
Then again, lossless knowledge compression doesn’t lose info. As a substitute, it makes use of strategies to characterize the unique info utilizing much less knowledge [7]. Nevertheless, the quantity of compression that’s doable utilizing lossless knowledge compression is way decrease than that of lossy compression.
Though k-means is a type of lossy compression, the lack of element may be virtually in-perceivable to the human eye for sure values of okay.
Are you able to discover many variations between the 2 photos above? Utilizing okay=256, the compressed picture on the suitable requires just one/3 the quantity of information in comparison with the complete picture on the suitable!
Randomness in Centroid Initialization
Holding every thing with reference to k-means fixed, every run will differ barely because of the randomness inherent within the centroid initialization course of.
Which means the compressed photos given the identical parameters will output barely totally different variations. Nevertheless, for bigger values of okay, this impact isn’t as obvious to the human eye.
Now that we’ve got accomplished a radical evaluation of the k-means algorithm with reference to picture compression, we are going to explicitly talk about its benefits and drawbacks.
Benefits
- Effectivity: The k-means algorithm is computationally environment friendly (linear time complexity), making it appropriate for real-time picture compression functions [8]. This additionally means it could actually deal with giant photos.
- Simplicity: The k-means algorithm is comparatively easy and simple to know.
- Nice for sure kinds of photos: k-means performs nicely on photos with distinct clusters of comparable colours.
Disadvantages
- Lossy Compression Algorithm: Okay-means is a type of lossy compression that represents a whole picture primarily based on clusters of pixels, due to this fact it loses some coloration info and will not protect tremendous particulars in a picture.
- Sensitivity to initialization: The efficiency of the k-means algorithm may be delicate to the preliminary positions of the centroids, which might result in sub-optimal or inconsistent outcomes. That is much less of an issue with bigger values of okay.
- Not appropriate for sure kinds of photos: k-means algorithm carry out poorly on photos with clean coloration gradients and pictures with excessive noise.
General, k-means could be a good selection for lossy picture compression, particularly for photos with distinct clusters of comparable colours. Nevertheless, it is probably not the only option for all sorts of photos and different strategies comparable to vector quantization or fractal compression could produce higher outcomes.
The consumer has a crucial resolution to make when choosing the worth of okay, and should take note the ‘compression quantity vs. element trade-off’ mentioned within the “Choosing ‘okay’” part. The optimum okay worth will possible fluctuate in keeping with the consumer’s wants.
Hopefully the totally different visualizations had been in a position to assist develop a stronger understanding of the k-means algorithm, and the way it can carry out picture compression.
References
[1] Krishna, Okay., and M. Narasimha Murty. “Genetic Okay-Means Algorithm.” IEEE Transactions on Programs, Man and Cybernetics, Half B (Cybernetics), vol. 29, no. 3, 1999, pp. 433–439., https://doi.org/10.1109/3477.764879.
[2] https://stats.stackexchange.com/questions/188087/proof-of-convergence-of-k-means
[3] Ng, Andrew. “CS229 Lecture Notes.” https://cs229.stanford.edu/notes2022fall/main_notes.pdf
[4] My Github Repository with the code for this mission. https://github.com/SebastianCharmot/kmeans_image_compression
[5] Gan, Guojun, and Michael Kwok-Po Ng. “Okay -Means Clustering with Outlier Elimination.” Sample Recognition Letters, vol. 90, 2017, pp. 8–14., https://doi.org/10.1016/j.patrec.2017.03.008.
[6] “Lossy Compression (Article).” Khan Academy, Khan Academy, https://www.khanacademy.org/computing/computers-and-internet/xcae6f4a7ff015e7d:digital-information/xcae6f4a7ff015e7d:data-compression/a/lossy-compression.
[7] Ming Yang, and N. Bourbakis. “An Overview of Lossless Digital Picture Compression Methods.” forty eighth Midwest Symposium on Circuits and Programs, 2005., 2005, https://doi.org/10.1109/mwscas.2005.1594297.
[8] Chiou, Paul T., et al. “A Complexity Evaluation of the JPEG Picture Compression Algorithm.” 2017 ninth Laptop Science and Digital Engineering (CEEC), 2017, https://doi.org/10.1109/ceec.2017.8101601.