Sorting algorithms are the means to kind a given set of information in an order in keeping with the requirement of the consumer. They’re primarily used to kind information in an rising or reducing method. There are two forms of sorting algorithms:
- Comparability-based sorting algorithms
- Non-comparison-based sorting algorithms
Comparability-based sorting algorithms: The weather of an array are in contrast to one another to kind the array. Such a algorithm checks if one factor is larger than or equal to a different factor within the array. It doesn’t do manipulation on a single array factor.
Examples of comparison-based algorithms: Merge kind (examine the weather and duplicate them), Quicksort (examine the weather and swap them), and Heap kind (Heapify the weather utilizing comparability).
Theorem: Each comparison-based sorting algorithm has the worst-case operating time of
Proof:
Allow us to assume a comparison-based sorting algorithm, and an array of size N. Contemplate the enter array accommodates array components like 
in some jumbled order. We are able to order these N components in N! other ways.
- Assumptions:
- Proof: By the Pigeonhole precept: If n gadgets are put into m containers, with n > m, then no less than one container should comprise a couple of merchandise.
- Right here, the pigeon is N! totally different inputs. The holes are 2Ok totally different executions.
- If
*** QuickLaTeX can not compile formulation: *** Error message: Error: Nothing to indicate, formulation is empty
, This implies the algorithm executes identically on 2 distinct inputs, and we are able to’t have a standard execution of the sorting algorithm, which is averse to our assumption of a sorting algorithm.
- For the reason that sorting methodology is appropriate, 2Ok ≥ N! ≥ (N/2)N/2, as a result of there are no less than N/2 phrases in N * (N – 1) * . . . * 2 * 1 that has a price of no less than N/2.
- Taking log base 2 on each side, Ok = (N/2)log2(N/2)
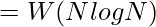
- Therefore, each comparison-based sorting algorithm has the worst-case operating time that may by no means be higher than
.
