Catching the high-level concept and implement an oracle for SAT situations
At the start of my journey in Quantum Computing, I used to be confused about what an “oracle” was. Sometimes, you learn one thing like:
“(…) then, due to the oracle, you’ll be able to determine the answer.”
In the long run, the one factor that I understood was that:
“It is ready to catch the answer of a given drawback (in some way)”.
However, I didn’t know how. Thus, questions just like the followings come up.
What does this “oracle” appear to be?
How can I determine one thing that I don’t know a priori?
These are authentic questions! We’ll discover out the reply to all these questions! Specifically:
- We’ll perceive why oracles are vital.
- We’ll catch the high-level instinct behind an oracle.
- We’ll present outline an oracle capable of clear up a Boolean Satisfiability Drawback (SAT)
- Moreover, an implementation in Qiskit shall be supplied!
Earlier than to start out, you want only a few stipulations:
- What superposition is.
- What quantum gates like H, X, CX are.
- What quantum circuits are.
The goal of this text is to offer a self-contained presentation of Grover’s Algorithm. We’ll keep away from mathematical particulars as a lot as attainable, thus offering a sensible concept of the facility of this quantum algorithm.
The “oracle” is a part of Grover’s Algorithm: one of the vital disruptive quantum algorithms and one of many the reason why quantum computing attracts lots of curiosity.
What’s the energy of Grover’s Algorithm?
Allow us to say we have to discover a particular goal factor in an unstructured set of N components.
In classical computing, since we’ve no prior information about the place this goal factor is situated, we would want to take a look at each single factor.
For instance, suppose on the lookout for the quantity 3 in an unsorted array (Determine 1).

The price is O(N) (i.e., within the worst case, we have to scan all of the N components).
In quantum computing, due to Grover’s Algorithm, it’s attainable to retrieve the answer in O(√N). We achieved a quadratic speedup with respect to classical computing (Determine 2)!

A little bit background
Sometimes, quantum computer systems should run a given quantum algorithm greater than only a single time. Generally they return the right output, and typically they don’t.
Thus, our goal is to extend (or “amplify”) the probabilities of getting the right output (Determine 3).
The purpose is that:
We wish a likelihood distribution of the outputs from quantum computer systems such that the likelihood of getting the resolution in a given run of the algorithm is increased than the considered one of getting an invalid output.
.. For the reason that likelihood of getting a flawed output is non-zero, extra runs could be required.

Grover’s Algorithm is fabricated from two elements: an Oracle and a Diffuser.
ORACLE
- The Oracle “marks” the answer(s) (Determine 4).

Because of the oracle, we’re capable of mark the right factor amongst all of the N components of an unstructured set of information. (Don’t paw! I’ll inform you shortly what the oracle seems like 
Nevertheless, the oracle alone isn’t sufficient.
In actual fact, the oracle simply marks the right factor, however it doesn’t enhance the likelihood of getting this factor because the output of the quantum algorithm. Certainly, the oracle alone could be ineffective for the reason that likelihood of getting this factor could be 1/N (i.e., at random!).
Visible Instance
Allow us to say that we’ve N=7 components, and we search for the factor “triangle rectangle” (i.e., our resolution). Thus, we apply the oracle that marks “triangle rectangle”.
Nevertheless, the likelihood of getting the triangle rectangle is 1/7 (Determine 5), which is identical as getting considered one of all the opposite components!

Right here the Diffuser involves the rescue! In actual fact, it is ready to enhance the probabilities of getting the triangle rectangle!
THE DIFFUSER
- The Diffuser “amplifies” the answer(s) (Determine 6).

Why the Diffuser works, is out of the scope of this text. For these curious, I’ll present you some references on the finish of this text.
The purpose is that it will increase the probabilities of getting the factor marked by the oracle as output (Determine 7).

Nevertheless, don’t panic! The Diffuser implementation is identical for each oracle, and I’ll present the code on the finish! Promise!
We are able to set the Diffuser apart and transfer to reply the query:
“What does an oracle appear to be”?
Behind the Oracle
I discovered the identify “oracle” somewhat deceptive. It appears that there’s somebody that may provide the resolution by simply asking: “What’s the resolution?”.
I want to image in my thoughts the picture of a filter! It’s as much as you to handcraft a filter that has the precise form of the factor you search for (Determine 8)!

Why a filter?
Properly, earlier than operating Grover’s Algorithm, in some sense, you possess all the weather (I’ll clarify how later, however it’s fairly easy), and also you wish to filter out those that aren’t your resolution.
Nonetheless, take into account that you, and solely you, rigorously outline this filter.
Now, a query could come up:
I’ve to design a filter that is ready to catch the answer and reject all the opposite components. However to have the ability to catch the answer, I have to know the answer, proper?
Thus, which means I already know the answer. So…
What’s the purpose of this algorithm?
That may be a authentic concern!
One Step again
Grover’s Algorithm’s unique identify is “A quick quantum mechanical algorithm for database search.” Thus, the examples I discovered had been on on the lookout for a quantity in a set of numbers.
If you wish to discover quantity 3 in a dataset, you already know the answer a priori. You had been defining an oracle that caught for quantity 3, and the output was 3. Nothing too thrilling within the first occasion, proper?
[Small Note 1] In Grover’s algorithm, you’ll want to know a priori {that a} resolution exists (truly, you’ll want to know the precise variety of options).
[Small Note 2] There are different quantum algorithms that discover out the variety of options to a given drawback. Then, you should utilize Grover’s algorithms.
Two Step forward
The turning level is that the oracle generally is a perform, not only a quantity! On this case, we discuss with the Amplitude Amplification algorithm, which we are able to think about as a generalized Grover’s Algorithm.
What do you plan for “an oracle generally is a perform”?
For instance, we are able to ask our quantum pc: “What’s that factor better than 5 and fewer than 6”?
x > 5 ∧ x < 6
The psychological step is small, however the level is that we don’t have to know the answer, which shall be your oracle! Therefore, acquiring a quadratic pace up with respect to the classical brute pressure algorithm! Now It’s time to cease merely speaking and begin appearing.
A SAT drawback consists to find an project of variables such that it satisfies a given Boolean method. (I recall you that SAT belongs to the NP-complete class, a really attention-grabbing drawback!)
For instance, in (¬ x1 ∧ x2), the project that satisfies the boolean method is:
x1=False, x2=True
Specifically, we deal with a specific type of Boolean method, the Conjunctive Regular Kind (CNF) or Clausal Regular Kind.
CNF Refresh
The CNF consists of conjunctions of a number of clauses.
- Every clause incorporates a number of literals (boolean variables).
- A CNF incorporates solely the operators: ¬(not), ∨ (or), ∧ (and).
- The conjunctions of clauses are obtained via the ∧ operator.
- The literals of every clause are associated by the ∨ operator
- The ¬ operator can solely be used as a part of a literal.
Instance of a CNF:
(x ∨ y) ∧ ¬y
The answer project is: x=True, y=False
We’ll outline the quantum circuit that solves the above CNF.
Earlier than beginning, allow us to rewrite the CNF occasion above when it comes to AND utilizing De Morgan guidelines (Determine 9). Why? Simply because it is going to be simpler to explain the oracle later

Thus, we rewrite (x ∨ y) ∧ ¬y as ¬(¬x ∧¬y) ∧ ¬y.
Specifically, we’ll outline an oracle that marks the answer of:
¬(¬x ∧¬y) ∧ ¬y
For simplicity, allow us to assume that we already know that the above occasion has a single resolution. On the finish of the article, I’ll clarify why we make this assumption.
- 1) Generate all of the attainable assignments for the boolean method: ¬(¬x ∧¬y) ∧ ¬y.
- 2) Apply the Oracle.
- 3) Apply the Diffuser.
- 4) Carry out measurements.
NOTE
Sometimes, we have to repeat steps 2) and three) various occasions in accordance with the method:
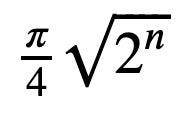
the place n is the variety of variables.
In our instance, n=2 (i.e., x and y). Thus, the variety of repetitions is 1. That’s, we apply only one time the oracle and the diffuser.
If you wish to study extra about how this method is obtained, I’ll go away you some references on the backside of the article.
STEP 1: Generate all of the attainable assignments for the boolean method
We put into superposition all of our qubits via Hadamard gates (Determine 10)! That’s, we generate all the attainable assignments for our boolean method.

Since we all know {that a} resolution exists, then our resolution is inside the assignments (Determine 11) we generated by placing into equal superposition all of the qubits.

STEP 2: Apply the Oracle
I wish to stress that, on this instance, we have no idea the answer like within the instance “Search for quantity 3”.
Typically, by defining the SAT occasion, we simply outlined the situation that the enter has to fulfill to be our resolution (i.e., your oracle/your perform!)
Follows the oracle circuit (Determine 12).

Don’t panic! We’re going to analyze intimately the entire circuit
DETAILS
We observe 3 extra qubits within the oracle circuit, respectively:
- 2 working qubits w.
- a qubit checker.
Working qubits
We add as many working qubits w because the variety of clauses of the CNF occasion. The scope of working qubits is to retailer the output of a given clause quickly.
In our instance, ¬(¬x ∧¬y) ∧ ¬y, we’ve 2 clauses then 2 working qubits w are wanted.
Checker qubit
The aim of the qubit checker is to mark the right resolution. That’s, when a variables project satisfies the oracle circumstances, then the checker is flipped to 1.
CLAUSES
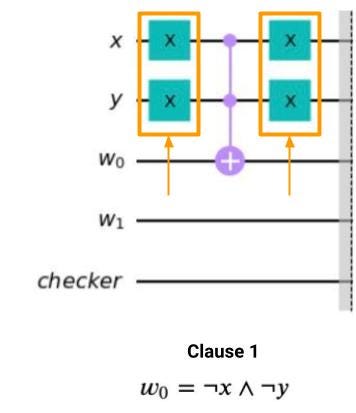
We break down ¬(¬x ∧¬y) ∧ ¬y into three elements (Determine 13):
- Clause 1. w0 = ¬x ∧¬y
- Clause 2. w1 = ¬y
- Consequence. ¬w0 ∧ w1
Observe that w0 corresponds to ¬x ∧¬y and to not ¬(¬x ∧¬y)!
We postponed the primary ¬ to ¬w0 ∧ w1.

Clause 1. w0 = ¬x ∧¬y
Clause 1 checks the situation ¬x ∧¬y (Determine 14). It’s applied via a MultiControlled-X gate the place:
- x and y are the management qubits,
- w0 is the goal qubit that shops the results of the situation ¬x ∧¬y.
Please word that the MultiControlled-X gate should set off when ¬x and ¬y. To take action, we prepend and append two X gates respectively to x and y, thus negating them.
Clause 2. w1 = ¬y
Clause 2 checks the situation ¬y (Determine 15). It’s applied via a Managed-X gate the place:
- y is the management qubit,
- w1 is the goal qubit that shops the results of the situation ¬y.
As earlier than, since we search for the clause ¬y, thus we negate the qubit y within the Managed-X gate.

Consequence. ¬w0 ∧ w1
Consequence checks the situation ¬w0 ∧ w1 which corresponds to our CNF occasion ¬(¬x ∧¬y) ∧ ¬y (Determine 16). The situation ¬w0 ∧ w1 is applied via a MultiControlled-X gate the place:
- w0 and w1 are the management qubits,
- checker is the goal qubit that flips to 1 if ¬w0 ∧ w1 is glad.
We recall that w0 corresponds to ¬x ∧¬y and to not ¬(¬x ∧¬y).
Subsequently, we have to negate w0: ¬(¬x ∧¬y) = ¬w0.

UNCOMPUTATION
The oracle’s final step frees the working qubits w0 and w1. That is achieved by performing uncomputation (Determine 17).
To uncompute w0 and w1 it’s enough to use the gates implementing Clause 1 and Clause 2 in reversed order.

Finally, we handcrafted our oracle! The magic has been revealed!
STEP 3: Apply the Diffuser
Final, we apply the Diffuser operator, which amplifies the right resolution (Determine 18).

STEP 4: Measurement
Finally, we measure qubits x and y (Determine 20).

The output distribution comply with in Determine 21.

The very best likelihood corresponds to the project y=0 (False), x=1(True) (i.e., 01).
Specifically, the project 01 satisfies our CNF occasion ¬(¬x ∧¬y) ∧ ¬y!
The primary goal of this text is to present a self-contained presentation of oracles and implement them utilizing Qiskit. Specifically:
- We catch the concept of what Oracles are.
- The aim of the Diffuser.
- Easy methods to successfully implement an Oracle and a Diffuser in Qiskit.
Within the references under, you’ll find my Github repository with the Qiskit implementation in an effort to play with it
AH! Within the offered instance, the variety of options was precisely 1. Nevertheless, we are able to have a couple of resolution for a given drawback! In these instances, we have to make a small change within the method that computes the variety of repetitions of the couple Oracle-Diffuser. Specifically, the method turns into:

Within the Github repository, additionally, you will discover an instance of a CNF occasion with a couple of resolution to play with it.




