A computationally efficient approach of finishing up Bayesian statistics
In Bayesian statistics, the conjugate prior is when the posterior and prior distributions belong to the identical distribution. This phenomenon permits for less complicated calculations of the posterior making Bayesian inference so much simpler.
On this article, we are going to achieve an in-depth view of the conjugate prior. We’ll present the necessity for it, derive an instance from first ideas and at last apply it to an actual world drawback.
Bayes’ Theorem
Lets have a fast recap over Bayes’ theorem:

- P(H): The prior. The chance of the speculation, H.
- P(D|H): The probability. The chance of the information, D, given our present speculation, H.
- P(H|D): The posterior. The chance of the present speculation, H, given the information, D.
- P(D): The normalising fixed. This is the sum of the merchandise of the likelihoods and priors which is named the Regulation of complete chance:

If you would like a extra in-depth derivation and understanding of Bayes’ theorem, take a look at my earlier article right here:
Bayesian Updating
We use Bayes’ theorem to replace our perception a few sure occasion once we obtain extra information about it.
Basically we supply out the replace as follows:

Then when new information arrives, the posterior turns into the brand new prior. This course of is consistently repeated with new information, therefore it’s referred to as Bayesian updating. That is in essence what Bayesian inference is.
You possibly can learn extra about Bayesian updating right here:
Nevertheless, if we need to acquire legitimate possibilities we have to compute P(D). As displayed above, that is the sum of the merchandise of the likelihoods and priors. One other approach of describing the summation is thru an integral:

This integral is commonly intractable. This principally means it is vitally computationally costly or it doesnt have a closed type resolution. I’ve linked right here a StatExchange thread that explains why it’s intractable.
Background
Conjugate priors is a technique of getting across the intractable integral problem in Bayesian inference. That is when each the prior and posterior are of the identical distribution. This permits us to simplify the expression of calculating the posterior. Within the subsequent part we are going to present this phenomenan mathematically.
Binomial and Beta Contingency
One of many easiest and customary conjugate distribution pair is the Beta (prior) and Binomial (probability).
Beta Distribution:
- Known as the distribution of possibilities as a result of its area is bounded between 0 and 1.
- Conveys the essentially the most possible possibilities concerning the success of an occasion.
Its chance density operate (PDF) is written as:

Right here x is bounded as 0 ≤ x ≤ 1, so it will possibly simply be interpreted as chance and B(α, β) is the Beta operate.
If you would like a full run down on the Beta distribution, you must skim over my earlier article on it:
Binomial Distribution:
- Conveys the chance of a sure variety of successes ok from n trials the place the chance of success is x.
PDF:
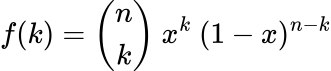
Essential Level
- The important thing distinction between the Binomial and Beta distributions is that for the Beta distribution the chance, x, is a random variable, nonetheless for the Binomial distribution the chance, x, is a hard and fast parameter.
Relation To Bayes
Now let’s undergo some enjoyable maths!
We are able to rewrite Bayes’ theorem utilizing the chance of success, x, for an occasion and the information, ok, which is the variety of successes we observe:
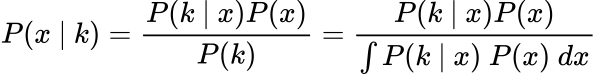
Our posterior is principally the chance distribution over all of the attainable possibilities of the success charge. In other-words, the posterior is a Beta distribution.
We are able to specific the above equation utilizing the Binomial distribution as our probability and the Beta distribution as our prior:

Yeah, doesn’t look that good. Nonetheless, we are actually going to simplify it:

A few of you could discover one thing particular about that integral. It’s the definition of the Beta operate!

Due to this fact, the ultimate type of our posterior is:

A Beta Distribution!
Voilà, we have now simply gone from a Beta previous to a Beta posterior, therefore we have now a conjugate prior!
In case you are extra concerning the Beta-Binomial conjugate prior, there’s a nice on-line ebook that describes their relationship in depth right here.
Why Is It Helpful?
You could be scratching your head questioning why I’ve taken you thru this terrible derivation simply to get one other model of a Beta distribution?
What this lovely consequence reveals us, is that to do a Bayesian replace we not have to compute the product of the probability and prior. That is computationally costly and generally not possible as I mentioned earlier. We are able to now simply use easy addition!
Downside Background
In Main League Baseball (MLB), the speed the batters hit the ball divided by the variety of balls they’re pitched is named batting common. The batting common in 2021 within the MLB was 0.244 (24.4%).
A participant begins the season very effectively and hits his first 3 balls. What would his batting common be? A frequentist would say it’s 100%, nonetheless us Bayesians would come to a distinct conclusion.
Prior
We all know that the batting common is 0.244, however what concerning the attainable vary of values? A good common is taken into account to be round 0.3, which is the higher vary and one under 0.2 is taken into account to be fairly dangerous.
Utilizing these values we will assemble an appropriate Beta prior distribution:
from scipy.stats import beta as beta_dist
import matplotlib.pyplot as plt
import numpy as npalpha = 49
beta = 151
chance = np.arange (0, 1, 0.001)
prior = beta_dist.pdf(chance, alpha, beta)plt.determine(figsize=(12,6))
plt.plot(chance, prior, linewidth=3)
plt.xlabel('Batting Common', fontsize=20)
plt.ylabel('PDF', fontsize=20)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.axvline(0.244, linestyle = 'dashed', shade='black', label='Common')
plt.legend(fontsize=18)
plt.present()

This appears affordable as our vary is fairly confined between 0.2 and 0.3. There was no specific cause why I selected the values of α=49 and β=151, they simply satisify what we all know concerning the prior distribution.
Nevertheless, that is usually the argument made towards Bayesian statistics. Because the prior is subjective, then so is the posterior. This implies chance is not goal, however moderately a private perception.
Chance and Posterior
The probability of the information is that the brand new participant has hit 3 from 3, subsequently they’ve have an additional 3 successes and 0 failures.
Utilizing our information of the conjugate prior, we will merely add an further 3 to the worth of α and 0 to β:
alpha = 49
beta = 151
new_alpha = 49+3
new_beta = 151
chance = np.arange (0, 1, 0.001)
prior = beta_dist.pdf(chance, alpha, beta)
posterior = beta_dist.pdf(chance, new_alpha, new_beta)plt.determine(figsize=(12,6))
plt.plot(chance, prior, linewidth=3, label='Prior')
plt.plot(chance, posterior, linewidth=3, label='Posterior')
plt.xlabel('Batting Common', fontsize=20)
plt.ylabel('PDF', fontsize=20)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.axvline(0.244, linestyle = 'dashed', shade='black', label='Common')
plt.legend(fontsize=18)
plt.present()

It is smart why the common has barely shifted as three balls shouldn’t be that many. What if we now stated the participant hit 40 out of 50 balls, what would the posterior now appear like?
alpha = 49
beta = 151
new_alpha = 49+40
new_beta = 151+10
chance = np.arange (0, 1, 0.001)
prior = beta_dist.pdf(chance, alpha, beta)
posterior = beta_dist.pdf(chance, new_alpha, new_beta)plt.determine(figsize=(12,6))
plt.plot(chance, prior, linewidth=3, label='Prior')
plt.plot(chance, posterior, linewidth=3, label='Posterior')
plt.xlabel('Batting Common', fontsize=20)
plt.ylabel('PDF', fontsize=20)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.axvline(0.244, linestyle = 'dashed', shade='black', label='Common')
plt.legend(fontsize=18)
plt.present()

We see a better change as we now have extra information.
With out Conjugate Priors
With out conjugate priors, we must compute the posterior utilizing the merchandise of the likelihoods and priors. Lets undergo this course of for the aim of completeness.
We’ll use the instance the place the participant hit 40 out of fifty balls. Our probability on this case is:

The place we have now used the Binomial chance mass operate (PMF).
Peforming the Bayesian replace and plotting the posterior:
alpha = 49
beta = 151chance = np.arange(0, 1, 0.001)
prior = beta_dist.pdf(x, alpha, beta)
probability = 10272278170*chance**40*(1-probability)**10
posterior = prior*probability
posterior = posterior/sum(posterior)plt.determine(figsize=(12,6))
plt.plot(chance, posterior, linewidth=3, label='Posterior')
plt.xlabel('Batting Common', fontsize=20)
plt.ylabel('Likelihood', fontsize=20)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.axvline(0.244, linestyle = 'dashed', shade='black', label='Common')
plt.legend(fontsize=18)
plt.present()

We arrive on the identical distribution as earlier than!
The eager eyed of you could discover one distinction, the y-scale is totally different. That is associated to the SciPy Beta operate returning the PDF, whereas right here we’re working with the PMF.
Beta-Binomial aren’t the one conjugate distributions on the market:
Simply to call a couple of.
The unhappy half is that not all issues, in reality only a few, may be solved utilizing Conjugate priors.
Nevertheless, there are extra normal alternate options akin to Markov Chain Monte Carlo, which offer one other resolution to the intractable integral.
On this article, we described how conjugate priors permit us to simply compute the posterior with easy addition. That is very helpful, because it removes the necessity in calculating the product of the likelihoods and priors which may result in intractable integrals.
The total code used on this article may be discovered on my GitHub:

