A easy information from concept to implementation in Pytorch.

The trendy companies rely an increasing number of on the advances within the progressive fields like Synthetic Intelligence to ship one of the best product and providers to its prospects. Lots of manufacturing AI methods is predicated on varied Neural Networks skilled usually utilizing an amazing quantity of knowledge. For growth groups one of many largest challenges is learn how to practice their fashions in a constrained timeframe. There are numerous strategies and algorithms to do it however the most well-liked are these utilizing some sort of gradient descent methodology.
The coaching of Neural Networks (NN) based mostly on gradient-based optimization algorithms is organized in two main steps:
- Ahead Propagation — right here we calculate the output of the NN given inputs
- Backward Propagation — right here we calculate the gradients of the output with reference to inputs to replace the weights
Step one is normally simple to know and to calculate. The overall thought behind the second step can also be clear — we’d like gradients to know the course to make steps in gradient descent optimization algorithm. If you’re not acquainted with this methodology you’ll be able to verify my different article (Gradient Descent Algorithm — a deep dive).
Though the backpropagation just isn’t a brand new thought (developed in Nineteen Seventies), answering the query “how” these gradients are calculated offers some folks a tough time. One has to succeed in for some calculus, particularly partial derivatives and the chain rule, to totally perceive back-propagation working rules.
Initially backpropagation was developed to distinguish advanced nested features. Nevertheless, it turned extremely common because of the machine studying group and is now the cornerstone of Neural Networks.
On this article we’ll go to the roots and resolve an exemplary downside step-by-step by hand, then we’ll implement it in python utilizing PyTorch, and at last we’re going to check each outcomes to ensure all the things works tremendous.
- Computational Graph
Let’s assume we need to carry out the next set of operations to get our consequence r:
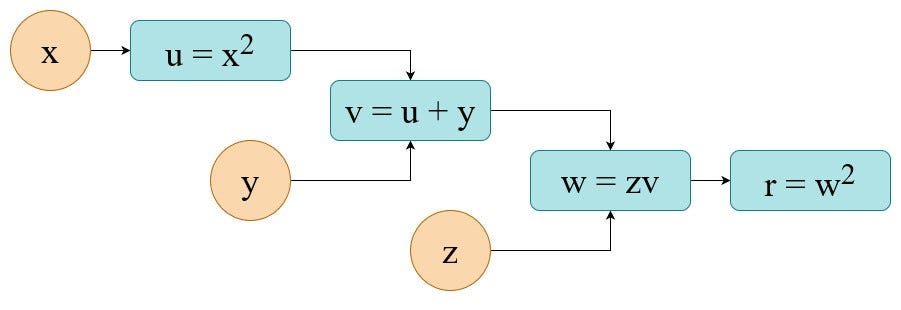
When you substitute all particular person node-equations into the ultimate one you’ll discover that we’re fixing the next equation. Being extra particular we need to calculate its worth and its partial derivatives. So on this use case it’s a pure mathematical job.

2. Ahead Move
To make this idea extra tangible let’s take some numbers for our calculation. For instance:
Right here we merely substitute our inputs into equations. The outcomes of particular person node-steps are proven beneath. The ultimate output is r=144.

3. Backward Move
Now it’s time to carry out a backpropagation, identified additionally underneath a extra fancy identify “backward propagation of errors” and even “reverse mode of computerized differentiation”.
To calculate gradients with reference to every of three variables now we have to calculate partial derivatives at every node within the graph (native gradients). Beneath I present you learn how to do it for the 2 final nodes/steps (I’ll go away the remainder as an train).
After finishing the calculations of native gradients a computation graph for the back-propagation is like beneath.

Now, to calculate the ultimate gradients (in orange circles) now we have to make use of the chain rule. In observe this implies now we have to multiply all partial derivatives alongside the trail from the output to the variable of curiosity:
Now we are able to use these gradient for no matter we would like — e.g. optimization with a gradient descent (SGD, Adam, and so on.).
4. Implementation in PyTorch
There are quite a few Neural Community frameworks in varied languages the place you’ll be able to implement such computations and make a pc to calculate gradients for you. Beneath, I’ll reveal learn how to use the python PyTorch library to resolve our exemplary job.
The output of this code is:
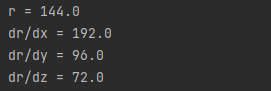
Outcomes from PyTorch are similar to those we calculated by hand.
Couple of notes:
- In PyTorch all the things is a tensor — even when it comprises solely a single worth
- In PyTorch if you specify a variable which is a topic of gradient-based optimization it’s a must to specify argument
requires_grad = True. In any other case, will probably be handled as mounted enter - With this implementation, all back-propagation calculations are merely carried out by utilizing methodology
r.backward()
5. Abstract
On this article we used backpropagation to resolve a particular mathematical downside — to calculate partial derivatives of a posh operate. Nevertheless, if you outline the structure of a Neural Community you might be de facto making a calculation graph and all of the rules seen right here nonetheless maintain.
In NNs the ultimate equation is then a loss operate of your selection, e.g. MSE, MAE and the node equations are principally weights/arguments multiplications adopted by varied activation features (ReLu, tanh, softmax, and so on.)
Hopefully, now you are feeling extra assured in answering the query of how the back-propagation works, why do we’d like it and learn how to implement it in PyTorch.
Completely satisfied coding!


