One tip to seek out common patterns like sine waves from randomness.
Anomaly detection in time sequence knowledge is a typical job in knowledge science. We deal with anomalies as knowledge patterns that exist not as anticipated. As we speak, let’s deal with detecting anomalies in a particular univariate time sequence generated by a stochastic course of.
The information ought to look noisy, chaotic, and random in these stochastic time sequence. Surprising adjustments must be taking place on a regular basis. If the worth will not be altering or altering with a deterministic sample, one thing is improper with the info.
Let’s check out the next plot and you will notice the labelled suspicious sections and perceive why they need to be detected as anomalies.

The above plot makes use of artificial knowledge generated by the code I’ll present subsequent. For patrons’ privateness, I received’t disclose the precise use case that impressed this method. I can attempt to give an instance:
The trail of a column of rising smoke might look weird and random relying on the various wind circumstances. It’s not possible you see repeating patterns like zigzags or lengthy straight strains except folks manipulate the ambiance.
I believe you bought the concept: we’re looking for certainties and patterns from a bunch of chaos and randomness, then these detected exceptions might be labelled as anomalies.
Generate artificial knowledge
The time-series knowledge above is generated by a random stroll course of. Then I randomly add three sections of a sine wave with Gaussian noise and one space with a relentless worth.
First, generate the time sequence.
Then, add 4 anomaly areas randomly.
Anomaly detection with spectral entropy
The anomaly sections have totally different lengths, frequencies and amplitudes. Can we discover these sections simply?
The reply is sure.
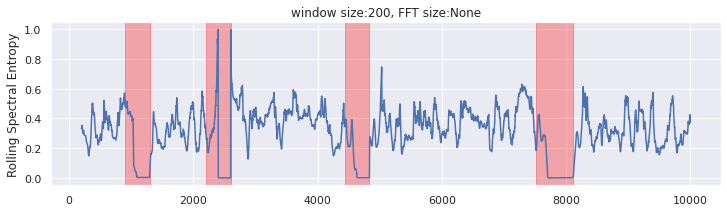
Merely computing a rolling spectral entropy might be a fast resolution. As you possibly can see within the plot, the rolling spectral entropy might be closed to zero for all of the anomaly areas. We are able to use the rolling entropy as a steady anomaly rating indicating the chance of anomaly.
Why spectral entropy works?
The concept is to compute spectral density first, normalize it, and at last compute the Shannon Entropy.
Right here I evaluate two examples of observations with the rolling window of 200. Above is a window in a single anomaly area, and beneath is a window in regular areas.


First, calculate the spectral density for every window and get the outcomes proven on the precise aspect.
Then chances are you’ll assume the frequency is a discrete variable with bins and deal with the normalized density because the likelihood for every frequency bin worth. As a result of the density is normalized, their sum must be equal to 1.
Now Shannon entropy can come to play.
“the Shannon entropy of a distribution is the anticipated quantity of data in an occasion drawn from that distribution. It provides a decrease sure on the variety of bits wanted on common to encode symbols drawn from a distribution P.”
Within the above anomaly window, the sign might be “lively” on the frequency bin of 1Hz solely (1Hz’s likelihood is sort of 1, others are practically 0). There aren’t any surprises, no uncertainties; subsequently, the entropy might be about 0 for this case.
The sign could also be “lively” at a number of frequency bins with totally different chances for the great area. Now we have extra uncertainties or unknown info, so increased entropy might be.
Rolling window measurement and FFT measurement
You don’t at all times see the spectral entropies extraordinarily near zero for these sine-wave-like anomalies. The rationale behind that is how we compute the spectral. There’s a probability that the height frequency might unfold into two neighbouring frequency bins (spectral leakage resulting from frequency decision). Then the Shannon entropy is not going to be near zero however will nonetheless be smaller than the instances in a traditional window.
The sampling charge and FFT measurement decide the frequency bins. If the FFT measurement will not be specified, we’ll use the window measurement.
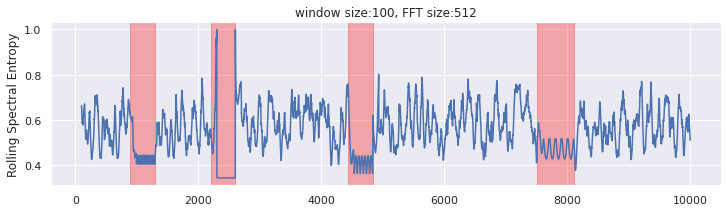
Above is the consequence with an FFT measurement of 512 and a window measurement of 100. We are able to nonetheless see the separation utilizing the rolling spectral entropy; though the anomaly areas’ scores are smaller, they aren’t 0. We might must do postprocessing like calculating the shifting common to phase the time sequence into the anomaly and commonplace sections. With a smaller window measurement, we are able to detect the anomaly earlier.
Within the precise utility, it’s best to discover and analysis the anomaly anticipated. Then you’ll choose the rolling window measurement or FFT measurement relying in your anomaly detection requirement.
Conclusion
Spectral entropy combines the concept of FFT, spectral density, and Shannon entropy. We are able to use it to test how a lot information comprises in a window of time sequence knowledge. Larger entropy implies uncertainty and randomness. Decrease entropy signifies common and deterministic patterns.
Subsequently we are able to detect patterns from randomness utilizing spectral entropy. In fact, spectral entropy works oppositely: detecting randomness from a sequence of patterned knowledge. However frequency evaluation perhaps performs effectively sufficient for these instances already.
Thanks for studying.
Have enjoyable together with your time sequence.


