The right way to discover time sequence correlation anomalies with practical examples

Entropy can separate randomness and certainties. In my earlier submit on Anomaly detection in univariate stochastic time sequence with spectral entropy, I present the magic of spectrum entropy. Now we are going to change the subject to anomaly detections in multivariate time sequence, and we’re nonetheless making an attempt to make use of entropy within the answer.
Multivariate time sequence have N time sequence variables. Every variable relies upon not solely on its previous values but additionally has some dependency on different variables. A typical anomaly is the interactions or dependencies of these variables will not be anticipated for some knowledge factors. There must be no obvious anomaly for any single variable. In any other case, the issue turns into univariate time sequence anomaly detection.
As an example, let’s discuss concerning the climate. Temperature and humidity are usually negatively correlated. Because the temperature will increase, the humidity will lower. So even when the temperature is fairly excessive, so long as the moisture stays within the decrease zone, matching the temperature accordingly, you’ll really feel sizzling. That’s a typical sizzling day, not an anomaly. I don’t know the place you reside, however you in all probability have skilled such days in summer season: days with very excessive temperatures and humidity concurrently, which made you are feeling exceptionally uncomfortable. That’s when the correlation of the time sequence of temperature and humidity went fallacious: an anomaly within the multivariate time sequence.
Correlation and Structural Entropy
Pearson correlation is an easy measurement for time sequence interactions. For a multivariate time sequence with N variables, we can have C(N,2) correlations (select two from N) or an N*N correlation matrix (higher triangle and decrease triangle are the identical).
We need to see how a lot information incorporates on this matrix. A typical technique is making use of a clustering algorithm to mine the structural info within the matrix. Beneath is an instance of utilizing hierarchical clustering on a correlation matrix.

Subsequent, we are going to apply the thought of entropy. Entropy may be outlined based mostly on the matrix’s construction, particularly, the variety of important clusters satisfying a sure threshold. Suppose all of the variables are extremely correlated. There might be just one cluster, and the correlation info contained within the multivariate time sequence is minimal. Within the different excessive case, all of the N time sequence will not be correlated, there might be N clusters, and the correlation info contained within the multivariate time sequence is most. Researchers proposed this entropy and named it Structural Entropy.
Utilizing structural entropy, we will remodel a bunch of time sequence right into a sign time sequence of entropy values, which captures the motion of the correlations of our curiosity. This transformation is especially useful if we need to monitor the correlations and catch anomalies. We’ll see that within the following two examples with real-world knowledge.
Path Dataset
We’ve the dataset of Seattle Burke Gilman Path. It was generated by monitoring the pedestrian and bikers on the path. The outline says, “Wires in a diamond formation within the concrete detect bikes, and an infrared sensor mounted on a wood submit detects pedestrians. The counters additionally seize the course of journey for each bikes and pedestrians”. This public dataset is offered for obtain from Kaggle.
The dataset has 4 columns: Ped South, Ped North, Bike North, and Bike South, which means the variety of folks of pedestrians/bikers within the south/north instructions. After aggregating for 2019 on the day stage, now we have a multivariate time sequence with 4 variables. Every time sequence has seasonality and development. Plot 1 reveals 4 density plots.

It’s anticipated that the variety of pedestrians/bikers in each instructions must be extremely correlated. As an example, if extra bikers present up on the southbound path on a pleasant climate day, extra bikers ought to present up on the northbound.
Plot 2 reveals the information as multivariate time sequence.
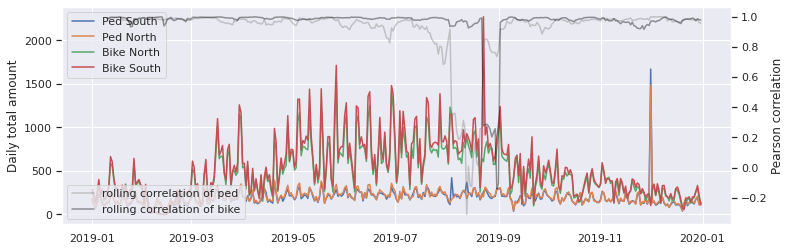
If we scrutinize the plot, we will eyeball some fascinating anomalies. For some days in August, whereas the variety of pedestrians going south went up, the variety of pedestrians going north went down. There are additionally comparable anomaly areas for the bikers in August.
To reveal these anomalies, I additionally plot two rolling correlations with a window measurement of 10 days on the second y-axis on the appropriate. These two gray traces clearly present the correlations altering in August.
Now let’s calculate structural entropy. There are two parameters concerned. The primary is the window measurement. Let’s nonetheless use 10 days. The second is the brink for clustering the correlation matrix. Since we consider the numbers in each instructions must be highly-correlated, let’s use 0.8. Plot 3 reveals the ultimate structural entropy curve.

We will see the spike in August, implying uncertainty of the correlations will increase. It could actually inform us extra info apart from the anomaly in August. For many days from March to August, the worth is 0. It implies the 4 variables are extremely correlated. For the remainder of the 12 months, the worth is spherical 1. It means there are two clusters within the matrix: Ped South and Ped North, and Bike South and Bike North. Typically, each instructions are correlated, however pedestrians and bikers will not be linked an excessive amount of. Perhaps the rationale behind that is the temperature and climate.
In late August, the entropy can go as much as 2. It implies there isn’t a explicit correlation among the many 4 variables. What occurred in August 2019? Ought to we deal with it as an actual anomaly?
Truthfully, I don’t know the rationale. I discovered ‘information’ after I searched “Seattle Burke Gilman Path 2019 August”: from August sixteenth to August 18th, the path was closed for tree elimination work. This occasion could trigger chaos lasting longer than three days. Individuals could detour after they see the work notification indicators and even after the job is finished. The areas of the work, the sensors and the indicators could impression how folks select the routes.
However from the information perspective, August certainly appears irregular. If we zoom in on the information for August, we are going to label August 4th, August thirteenth and August twenty fourth as obvious anomalies.

From this instance, we present that the structural entropy will catch the odd moments when the correlations of the multivariate time sequence change from predictable and deterministic into unpredictable and stochastic.
Subsequent is an instance of the opposite manner of anomaly.
Market Dataset
The concept of structural entropy was first utilized within the inventory market evaluation. On this instance, anomalies will seem as certainties from randomness or correlations from a bunch of uncorrelated.
I downloaded the worth historical past of round 400 main Canadian shares from Yahoo API. Then I calculated the each day return in share and obtained time sequence for every inventory. Plot 5 reveals 20 of these each day return time sequence.

Then we compute the structural entropy on all sequence and procure a brand new time sequence on entropy proven in Plot 6. Essentially the most important anomaly occurred round April 2020, when the market was severely hit by the covid 19. Round that interval, nearly all shares moved in the identical course: decrease. There was no uncertainty within the bear market, and the entropy was as soon as closed to zero. In different durations, the entropy worth varies between 4 and eight. That marks a daily market: some shares/sections are rising, and a few are falling.

Conclusion
Structural entropy supplies a strong device to detect anomalies in multivariate time sequence knowledge if the variables’ correlation is our concern. It could actually catch the second when correlated time sequence develop into uncorrelated and vice versa. It’s simple to grasp and compute. I like to recommend knowledge scientists discover this device for the duty of anomaly detection in multivariate time sequence.
I’ll share extra classes discovered for time sequence knowledge sooner or later.
Thanks for studying. Have enjoyable along with your time sequence knowledge.
References
Seattle Burke Gilman Path Knowledge (CC0: Public Area)
Yahoo Finance API (BSD 3-Clause “New” or “Revised” License)