How you can establish one of the best (and worst) activation features

Once I first began studying ML, I used to be instructed that activations are used to imitate the “neuron activations” within the mind, therefore the identify neural networks. It was not till a lot later that I discovered in regards to the finer intricacies of this constructing block.
On this article, I’ll clarify two key ideas and the instinct behind Activation features in Deep Neural Networks:
- Why we want them,
- Why we will’t simply choose any non-linear operate as activation.
All figures and outcomes on this article had been created by creator: Equations are written utilizing TeXstudio; fashions are created utilizing Keras, and visualized with Netron; and graphs are plotted utilizing matplotlib.

Terminology: An activation is a non-linear operate. Merely put, it’s any operate not of the shape y = mx + b.
In a Neural Community, these features are normally put after the output of every Convolution or Totally-Related (a.ok.a. Dense) layer. Their predominant job is to “activate the neurons”, i.e. seize the non-linearity of the mannequin.
However what’s non-linearity, and why is it vital?
Think about the next easy community with two Dense layers (you probably have labored on the MNIST dataset, this may increasingly look acquainted):

Let the enter be x, the load and bias of the primary layer be W_1, b_1, and of the second layer be W_2, b_2. With activation operate σ_1, σ_2, the output of the primary layer is:

And the output of the entire mannequin is:

However what if we didn’t use any activation operate? With out σ_1 and σ_2, the brand new output can be:
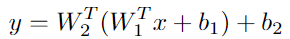
Discover that this equation could possibly be simplified to:

which is equal to a shallow community with one Dense layer. Merely put, the second layer didn’t add any helpful info in any respect. Our mannequin is now equal to:

We are able to generalize this evaluation to any arbitrary variety of layers, and the consequence will nonetheless maintain. (An identical consequence from Calculus: Composition of linear features remains to be a linear operate.)
So, for a Deep community to even make sense, now we have to use activations to every hidden output.
In any other case, we’ll find yourself with a shallow community, and the training functionality can be severely restricted.
Here’s a fast experiment on MNIST to additional illustrate the consequence:

For many sensible techniques/fashions, the activation is certainly one of these three: ReLU, Sigmoid, or Tanh (hyperbolic tangent).
ReLU
The only (and arguably greatest) activation. If an output of a hidden layer is adverse, we merely set it to zero:

And the graph of ReLU is:
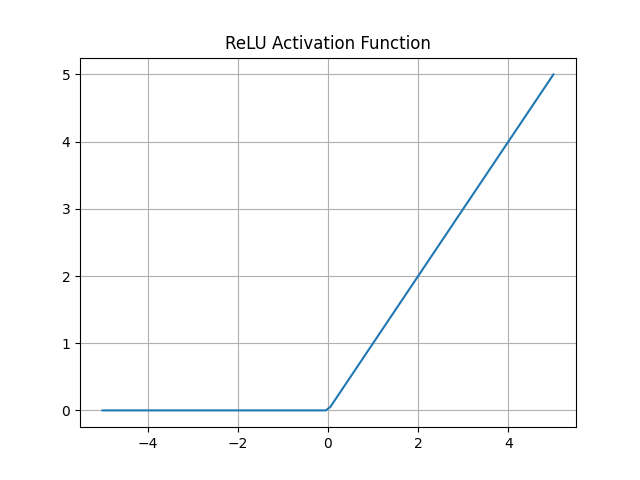
Professionals:
Cons:
- Lifeless ReLU: If all outputs are adverse, the gradient can be clipped to zero. This may be circumvented by higher weight initialization.
Sigmoid and Tanh
These features have the shape:

(Are you able to derive the derivatives of those features? Don’t fear, fashionable ML frameworks like PyTorch and TensorFlow present these activations without cost, with back-propagation already built-in and optimized.)
And their graph is:

They behave very equally, besides we cap the output between [0,1] for Sigmoid, and between [-1,1] for Tanh.
Professionals:
- Doesn’t blow up activation.
- Sigmoid is sweet for capturing “chances”, because the output is capped between 0 and 1. (These chances don’t sum as much as 1, we want Softmax activation for that.)
Cons:
- Slower back-propagation computation.
- Slower convergence in lots of circumstances.
- Vanishing gradient: the graph is flat when enter is way away from zero. This may be circumvented through the use of regularization.
In relation to non-linearity, just a few different features come to thoughts: quadratic, sq. root, logarithm…

Why will we not use these features in observe?
As a rule of thumb, a very good activation:
- Ought to be outlined for all actual numbers,
- Is differentiable, and back-propagation may be applied effectively,
- May be defined “heuristically”.
Some issues with the three features above are:
- Quadratic: provides no significant sign. An output of -2 or 2 will give the identical consequence.
- Sq. root: not outlined for
x < 0. - Logarithm: Not outlined for
x <= 0, this operate can be unbounded close to zero.
As a observe, you’ll be able to think about different non-linear features you could have encountered in Calculus/Linear Algebra. Take into consideration why we might not use them. That is one good train to enhance your instinct for Deep Studying.
For instance: Can I prolong the sq. root operate to adverse values (by drawing symmetrically) and use this as an activation operate?

(Trace: There’s something very mistaken with this activation operate!)
Activation operate is usually an afterthought in constructing Deep Studying fashions. Nonetheless, there’s some subtlety in its mechanics that you need to be conscious of. Hopefully, this text provides you a greater perception into the elemental concept of activations, and why we might select some features over others.
Comfortable studying!


