A fast tour to strengthen your basis in machine studying
Linear regression is extensively utilized by professionals in enterprise, science, engineering, and extra however not too many individuals perceive (or care) concerning the math underneath the hood. This text will information readers to the realm of math and hopefully to realize some math appreciation alongside the best way.
Linear Regression is a statistical mannequin that assumes the linear relationship between the enter x and the output y. The aim is to watch and predict.
Let’s say we’ve n observations x_i, y_i the place i = 1,…,n. We wish to provide you with a linear operate that may predict y_i primarily based on x_i,
the place, ŷ_i is the estimation of y_i. β_0 and β_1 are the y-intercept and slope that greatest match the linear regression line.
Every pair of β_0 and β_1 produce a unique line however we’re solely focused on one of the best line. What defines the “greatest” line? How do we discover one of the best “β_0” and “β_1”?
One strategy to measure the efficiency of linear regression is to seek out the error it produced. By including up all of the variations (residuals) between predicted values and precise values, we are able to have a grasp of what’s “dangerous”, and from that attempt to discover one of the best mannequin.

In different phrases, if y_i is the precise worth and ŷ_i is the anticipated worth, then the fee operate residual sum of sq. (RSS) is outlined as

We would like our prediction to be correct, which implies the error must be small. Thus, the aim is to seek out β_0 and β_1 such that the RSS operate G(β_0, β_1) is minimal.
In actual fact, there’s a closed components for β_0 and β_1,

Let’s uncover the place this components comes from and derive it from scratch!
Bear in mind in Calculus, to seek out the purpose the place the operate is minimal or most we’ve to seek out the important factors. Equally, if we all know what “dangerous” is, we are able to outline “greatest” by minimizing the badness.
We are able to discover the important level for the fee operate G utilizing partial derivatives. This important level is assured to be the worldwide minimal, since G is a convex operate. This level received’t be mentioned right here, however you possibly can visualize the fee operate as a skate park, and the worldwide minimal is the place gravitational power pulls you down ultimately.

Now again to the maths. As talked about above, the fee operate G is outlined by,

The partial spinoff of G with respect to β_0 is:

Setting ∂G/∂β_0 = 0 to acquire

Substituting β_0 = ȳ− β_1·x̄ into the G(β_0, β_1) we’ve,

Equally, differentiating G with respect to β_1 yields,
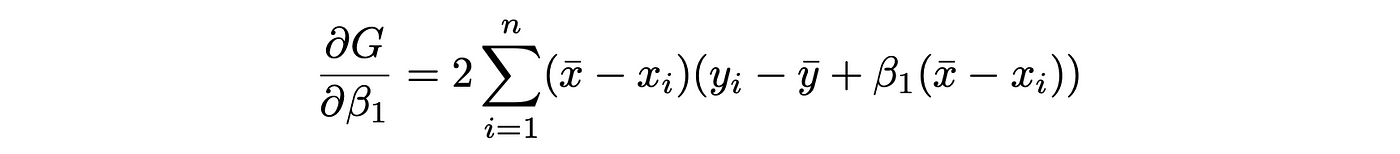
Setting ∂G/∂β_0 = 0 to acquire,
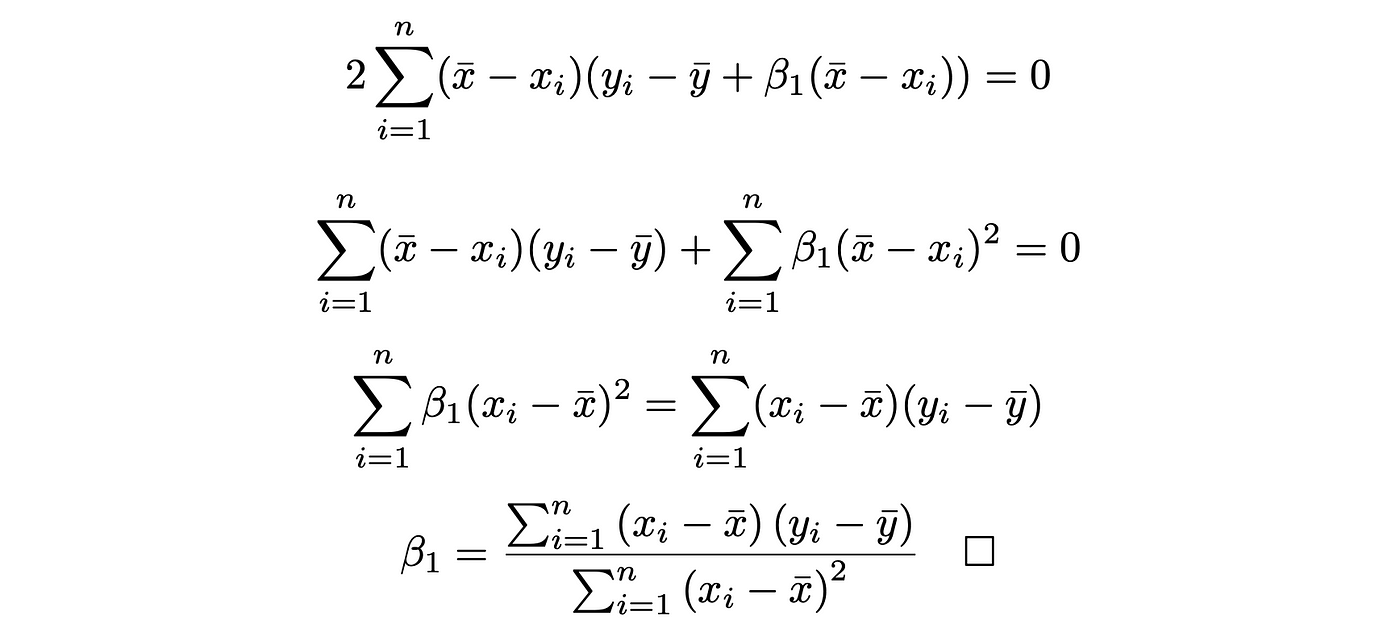
We’ve derived the components for a 2D linear regression utilizing Calculus. Theoretically, we are able to apply the identical process for 3D, or 4D. Because the variety of dimensions will increase, the complexity of the components will increase exponentially, thus it’s impractical to compute the components for a better dimension.
Totally different optimization methods have developed to unravel this downside. Certainly one of them known as gradient descent. However this shall be a unique matter for an additional time!
Thanks for studying.


