Time sequence are in all places. As information scientists, we’ve got varied time sequence duties, reminiscent of segmentation, classification, forecasting, clustering, anomaly detection, and sample recognition.
Relying on the info and the approaches, characteristic engineering could possibly be an important step in fixing these time sequence duties. Nicely-engineered options can assist perceive the info higher and increase fashions’ efficiency and interpretability. Feeding uncooked information to a black-box deep studying community could not work nicely, particularly when information is restricted or explainable fashions are most well-liked.
In case you have labored on characteristic engineering for time sequence, you most likely have tried constructing some primary options just like the imply, the variance, the lag, and the statistics primarily based on rolling home windows.
On this submit, I’ll introduce constructing options on spectral entropy. I recommend you embody it as one of many must-try options when your information is relevant (frequency area evaluation is smart). I’ll present how I tackled two classification issues on time sequence utilizing spectral entropy. I’ve proven easy methods to apply spectral entropy to an anomaly detection downside. Please consult with Anomaly Detection in Univariate Stochastic Time Sequence with Spectral Entropy.
My focus is on the appliance facet, so I’ll skip some primary introductions and theories.
Frequency area evaluation and spectral entropy
Usually, time sequence information is saved within the time area. The indexes are timestamps sampled with fastened intervals. A while sequence have waveform or seasonality, like sensory information (seismic vibrations, sound, and so forth.). We will suppose one thing is oscillating and producing the info like waves.
When sturdy wave patterns exist, reworking and analyzing the info within the frequency area will make sense. Quick Fourier Rework (FFT) is a basic method to remodel from the time area to the frequency area. Spectral entropy encodes the spectral density (distribution of energy within the frequency area) into one worth primarily based on Shannon entropy. If you’re within the elementary introduction, please verify Anomaly Detection in Univariate Stochastic Time Sequence with Spectral Entropy.
Right here is an analogy for a fast intro with out going deep into the formulation.
Suppose we research how individuals spend their spare time. One spends 90% on soccer. The opposite spends 90% on chess. Though their pursuits are totally different, it’s virtually sure that they may dedicate their spare time to their favorite hobbies. They’re comparable to some extent. This similarity is entropy. They may have the identical decrease entropy, implying decrease uncertainty.
One other individual spends 20% on mountaineering, 30% on studying, 20% on films, and 30 % on no matter. Apparently, the third individual is totally different from the primary two. We don’t know which exercise the third is doing precisely. On this case, the entropy is excessive, that means a better uncertainty.
Spectral entropy works the identical method. How the time is distributed corresponds to how energy is distributed throughout frequencies.
Subsequent, let’s see two real-world examples of how spectral entropy works wonders. The dataset is just not within the public area. Please permit me to make use of imprecise descriptions and conceal the dataset particulars.
Sign choice
The objective of this dataset is to construct a binary classifier with a complete of a whole lot of samples. Every pattern is a take a look at outcome labelled move or fail. One pattern has near 100 alerts. The size of the alerts is fixed. Determine 1 exhibits one instance (every small plot has three alerts).
If we extract X options from every sign, we can have 100*N options. Contemplating the small pattern dimension, we’ll run into the “curse of dimensionality” downside.
Since we’ve got super information for every pattern, let’s be selective and solely give attention to the alerts with essentially the most predictive energy and drop the irrelevant ones. I calculated spectral entropy for every sign, so we solely have 100 options. Then shallow timber are skilled.
From the highest vital options, solely three alerts present a excessive correlation with the labels. After I studied these alerts, I constructed personalized options in accordance. Lastly, I constructed a profitable mannequin with excessive efficiency. Furthermore, the mannequin solely requires round ten enter options, which advantages us with good generality and interpretability.
Frequency band choice
This instance is one other binary classification downside. Every pattern solely has one time sequence with totally different lengths. The whole pattern dimension is lower than 100.
The various size is just not a giant deal. We will cut up the time sequence into smaller fixed-length segments and use the pattern label because the phase label.
The little downside is that we’ve got a comparatively giant vary of frequencies. As a result of the sampling frequency is 48,000 HZ (which covers the sound that the human ear can hear), primarily based on the Nyquist theorem, the best frequency within the frequency area might be 24,000. Determine 2 is an instance.
I attempted the spectral entropy instantly however couldn’t clearly distinguish between positives and negatives. The primary cause is each labels have comparable peak frequencies and harmonics. The spectral distribution is an identical. In consequence, a spectral entropy on your complete frequency area received’t inform a big distinction.
For the reason that frequency decision is excessive, let’s zoom into sure frequency bands as an alternative of the entire spectrum. Hopefully, the delicate separations are hiding someplace.
I cut up the frequency into smaller bands. Every band is from X to X+100. So 24,000 will give us 240 bands. The upper frequencies contained solely noise with minimal energy. Subsequently, I ignored the upper frequencies noises, picked the decrease frequencies from 0 to three,000 and lower them into 30 bins. Then I calculated the spectral entropy for every band. Lastly, a tree-based mannequin was skilled utilizing solely 30 options. This strategy labored surprisingly nicely. Determine 3 exhibits the highest two options (spectral entropy of two bands). There’s a affordable boundary when utilizing solely frequency bands 1200 to 1300 and 2200 to 2300.
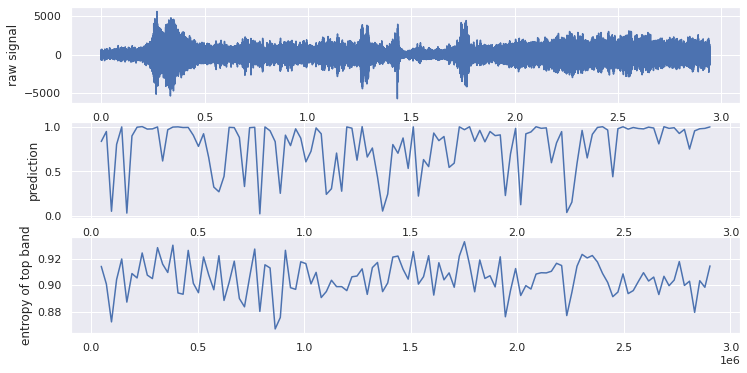
Determine 4 under exhibits the mannequin’s efficiency on take a look at information labelled optimistic. The highest plot is the uncooked sign. The center plot is the predictions for every phase. The underside is the entropy of frequency 1200 to 1300 for every phase. You possibly can see a lot of the predictions are near 1 and the entropy is probably going within the vary of 0.9 to 0.93. Determine 5 exhibits the take a look at information labelled unfavourable. Now the predictions drop to shut to 0, and the entropies differ within the vary of 0.8 to 0.9.
Conclusion
I present how spectra entropy helped me shortly discover a very powerful alerts and frequency bands for additional characteristic engineering.
In these two examples, we don’t have to make use of spectral entropy. As an illustration, we could construct options like the height frequency, the typical magnitude of frequency bands, and so forth. We will even have your complete frequency area information as one enter vector. In spite of everything, we are able to separate the targets within the frequency area.
I wish to discover options from the spectral entropy perspective as a result of:
It’s simple to interpret and compute.
It considerably compresses the data contained within the frequency area and retains the core data.
The draw back is a few information is misplaced. As an illustration, the worth of magnitude is just not thought-about in any respect.
Moreover, as a result of we remodel an inventory of values within the frequency area right into a sign worth, there’s a likelihood that totally different spectral distributions could have the identical entropy worth. That is like Hash Collision. For instance, a good coin and a biased coin have totally different entropy. However for a biased coin with a chance of X to heads and a second biased coin with a chance of Y to tails, their entropy would be the identical if X and Y are equal.
I hope you possibly can be taught the advantages of spectral entropy and apply it to your time sequence work sooner or later.
Thanks for studying.
Have enjoyable along with your time sequence.