An accessible introduction to a robust algorithm
Welcome again to the world of I-don’t-know-why-I-was-freaking-out-about-this-algorithm-because-I-totally-intuitively-get-it-now, the place we take difficult sounding Machine Studying algorithms and break them down into easy steps utilizing enjoyable illustrations.
At this time we’ll deal with one other clustering algorithm referred to as DBSCAN (Density-based spatial clustering of purposes with noise). To know DBSCAN higher, try the Okay-Means and Hierarchical clustering articles first.
Because the title suggests, DBSCAN identifies clusters by the densities of the factors. Clusters are normally in high-density areas and outliers are usually in low-density areas. The three most important benefits of utilizing it (based on the pioneers of this algorithm) are that it requires minimal area data, can uncover clusters of arbitrary form, and is environment friendly for big databases.
Now that we have now the introduction out of the way in which, let’s get to the enjoyable half — truly understanding how this works. Let’s suppose our uncooked information seems to be like this:
The very first thing to do is depend the variety of factors shut to every level. We decide this closeness by drawing a circle of a sure radius (eps) round a degree and every other level that falls on this circle is alleged to be near the primary level. As an example, begin with this pink level and draw a circle round it.
We see that this level overlaps, totally or partially, 7 different factors. So we are saying that the pink level is near 7 factors.
The radius of the circle, referred to as eps, is the primary parameter within the DSBCAN algorithm that we have to outline. We have to outline eps appropriately as a result of if we select a worth that’s too small, a big a part of the information is not going to be clustered. Then again, if we select a worth that’s too giant, clusters will merge and loads of information factors shall be in the identical cluster. Typically, a smaller eps worth is most well-liked.
Now think about this blue level. We see that it’s shut to three factors as a result of its circle with radius eps overlaps 3 different factors.
Likewise, for all of the remaining factors, we depend the variety of shut factors. As soon as we try this, we have to resolve what factors are Core Factors and what factors are Non-Core Factors.
That is the place our second parameter of the algorithm — minPoints — is available in. We use minPoints to find out if a degree is a Core Level or not. Suppose we set minPoints to 4 then we are saying {that a} level is a Core Level if a minimum of 4 factors are near it. If lower than 4 factors are shut to a degree, it’s deemed a Non-Core Level.
As a common rule, minPoints ≥ variety of dimensions in a dataset + 1. Bigger values are normally higher for datasets with noise. The minimal worth for minPoints have to be 3, however the bigger our dataset, the bigger the minPoints worth have to be.
For our instance, let’s set minPoints to 4. Then we will say that the pink level is a Core Level as a result of a minimum of 4 factors are near it, however the blue level is a Non-Core Level as a result of solely 3 factors are near it.
Finally, utilizing the above course of, we will decide that the next highlighted factors are Core Factors…
…and the remaining ones are Non-Core Factors.
Now, we randomly decide a Core Level and assign it to the primary cluster. Right here, we randomly choose a degree and assign it to the blue cluster.
Subsequent, the Core Factors which might be near the blue cluster, that means they overlap the circle with radius eps…
…are all added to the blue cluster:
Then, the Core Factors near the rising blue cluster are added to it. Beneath, we see that 2 Core Factors and 1 Non-Core Level are near the blue cluster, however we solely add the two Core Factors to the cluster.
Finally, all of the Core Factors which might be near the rising blue cluster are added to it and the information will seem like this:
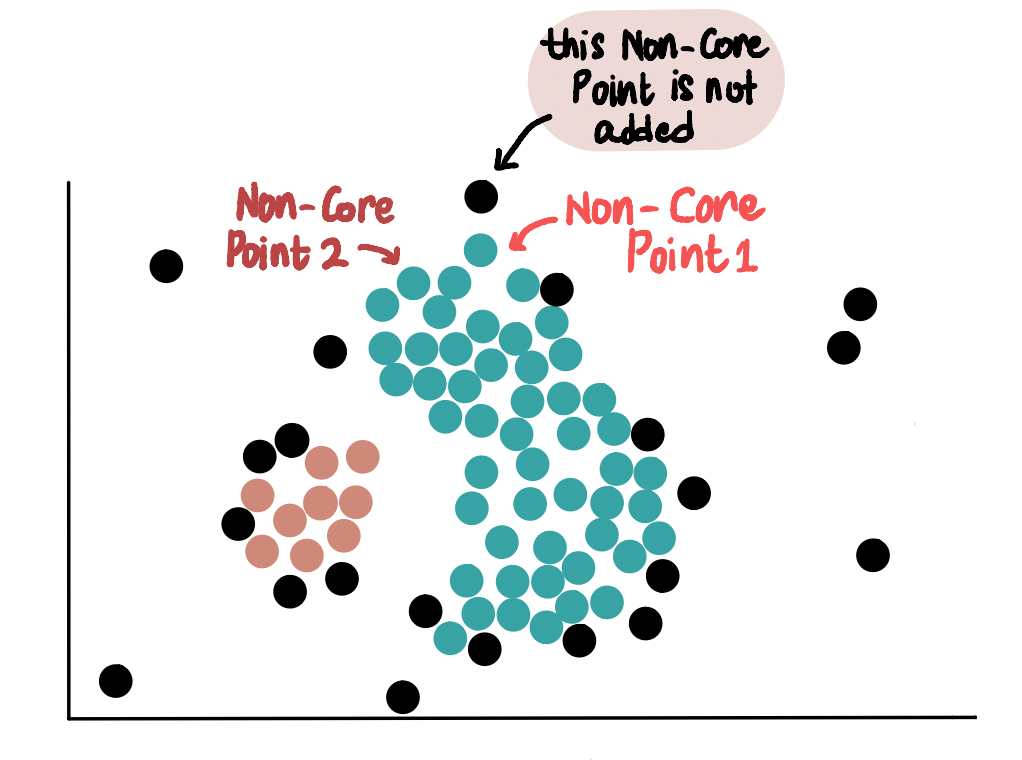
Subsequent, we add all of the Non-Core Factors near the blue cluster to it. As an example, these 2 Non-Core Factors are near the blue cluster, so they’re added to it:
Nevertheless, since they don’t seem to be Core Factors, we don’t use them to increase the blue cluster any additional. Which means this different Non-Core Level that’s near Non-Core Level 1 is not going to be added to the blue cluster.
So, not like Core Factors, Non-Core Factors can solely be a part of a cluster and can’t be used to increase it additional.
After including all our Non-Core Factors, we’re executed creating our blue cluster and it seems to be like this:
Now as a result of not one of the remaining Core Factors are near the primary cluster, we begin the method of forming a brand new cluster. First, we randomly decide a Core Level (that’s not in a cluster) and assign it to our second yellow cluster.
Then we add all of the Core Factors near the yellow cluster and use them to increase the cluster additional.
After which the Non-Core Factors which might be near the yellow cluster are added to it. After doing that, our information with the two clusters, seems to be like this:
We preserve repeating this course of of making clusters till we have now no Core Factors left. In our case, since all of the Core Factors have been assigned to a cluster, we’re executed making new clusters. Lastly, any remaining Non-Core Factors that aren’t near Core Factors and never a part of any clusters are referred to as outliers.
And similar to that we made our 2 clusters and located outliers AND got here out the opposite facet unscathed.
One could be inclined to ask — why DBSCAN over Okay-Means or Hierarchical clustering?
Okay-Means and Hierarchical are appropriate for compact and well-separated clusters and are additionally severely affected by noise and outliers within the information. Then again, DBSCAN captures clusters of advanced shapes and does an important job of figuring out outliers. One other good factor about DBSCAN is that, not like Okay-Means, we don’t must specify the variety of clusters (ok), the algorithm robotically finds clusters for us. The under determine illustrates some examples of the variations and why DBSCAN will be highly effective when used appropriately.