An intuitive rationalization
In my earlier article, I mentioned why it is best to desire reporting 95% confidence interval over p-value, particularly if you end up explaining the findings of your examine to non-statistician readers/audiences. On this article, I proceed the dialogue additional and attempt to present a bit extra readability.
Concerning the “right” interpretation of the boldness interval, considered one of my readers requested an amazing query:

As a scholar, I had the identical query for a very long time. Certainly, for many people, these are unintuitive ideas.
We now have the impression that statistics is about explaining information by means of cool graphs, estimating magical fashions, and many others. And all these statements are right. Nonetheless, after 4 years of training, my understanding is that, at its core, statistics is about lowering the complexity of a world stuffed with unknowns with the top aim of creating some subtle guesses about what we don’t know primarily based on what we all know by means of a scientific course of. Sadly, most people inherently desire certainty over uncertainty as a result of the latter makes us really feel uncomfortable. My speculation is that our want for “certainty” is without doubt one of the key explanation why many people wrestle to understand the basics of statistics.
Okay! Let’s concentrate on my reader’s concern now. Why do these two statements indicate various things? 🤔
Assertion 1: We’re 95% assured that the bowl accommodates the apple
Assertion 2: We’re 95% assured that the apple is within the bowl
These two statements seek advice from two totally different video games of uncertainties.
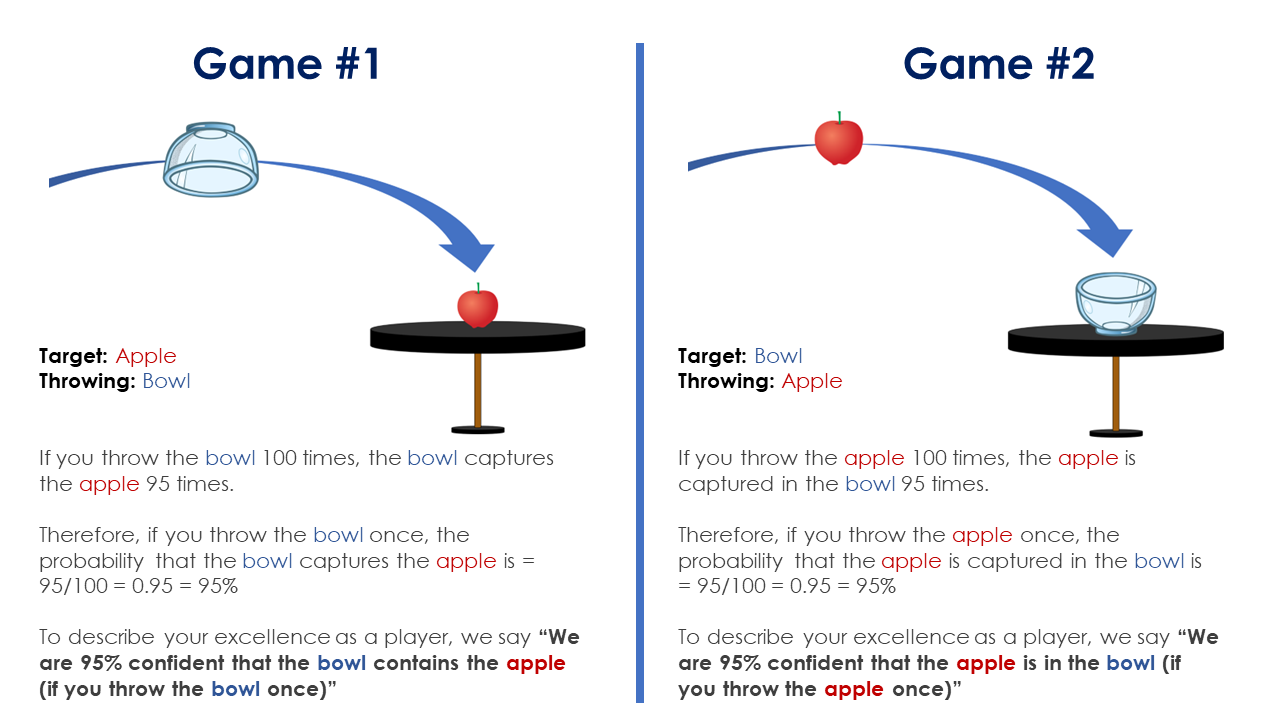
There’s an apple sitting nonetheless on a desk. The apple is the goal and it exists at a set location. There is no such thing as a uncertainty relating to the apple. It exists the place it exists.
As a participant, you get a bowl to throw on the apple. The aim is that the bowl captures the apple (the wrong way up).
You might be fairly good on the sport.
When you throw the bowl 100 occasions, the bowl captures the apple 95 occasions.
Due to this fact, when you throw the bowl as soon as, the chance that the bowl captures the apple is = 95/100 = 0.95 = 95%
To explain your excellence as a participant, we are saying “We’re 95% assured that the bowl accommodates the apple (when you throw the bowl as soon as)”.
There’s a bowl sitting nonetheless on a desk. The bowl is the goal and it exists at a set location. There is no such thing as a uncertainty relating to the bowl. It exists the place it exists.
As a participant, you get an apple to throw on the bowl. The aim is that the apple is captured within the bowl.
You might be fairly good on the sport.
When you throw the apple 100 occasions, the apple is captured within the bowl 95 occasions.
Due to this fact, when you throw the apple as soon as, the chance that the apple is captured within the bowl is = 95/100 = 0.95 = 95%
To explain your excellence as a participant, we are saying “We’re 95% assured that the apple is within the bowl (when you throw the bowl as soon as)”.
(1) The goal parameter has no uncertainty. It exists at a set place (at the very least we assume it does) at any given time limit.
(2) The factor which we’re throwing on the goal parameter has uncertainty relating to whether or not it captures the fastened goal or not🎯. Due to this fact, the assertion of chance must be with respect as to whether the thrown factor captures the fastened goal or not.
At a hypothetical college, the common weight (physique mass to be extra exact) of scholars is 130 lbs. It’s a fastened quantity (at any given time limit) however it’s unknown to you. As a researcher, you are attempting to estimate the inhabitants common weight.
There are 10,000 college students on the college and it isn’t potential so that you can weigh every particular person scholar and document their weight. You get a listing of all the scholars and randomly choose 100 of them.
All of them comply with allow you to measure their weight. And also you accumulate the knowledge. The pattern common weight is 125 lbs.
You understand that this is only one pattern — out of an infinite variety of samples that might have been drawn — from the goal inhabitants. When you draw one other pattern from the identical inhabitants, then the pattern common weight might be 132 lbs, or 120 lbs, or 142 lbs, or another worth. You wish to cut back this uncertainty by developing an interval of potential numbers.
Let’s assume, for the one pattern you chose, the 95% confidence interval is = [115 lbs, 135 lbs].
You say “ I’m 95% assured that *this interval* captures the true inhabitants common weight”.
This isn’t the identical as saying “I’m 95% assured that *the true inhabitants common weight* is captured within the interval.”
The true inhabitants common is your goal parameter which exists someplace within the universe and also you assume it’s a fastened quantity at any given time limit. As a result of it isn’t altering, the assertion on uncertainty shouldn’t be with respect to it.
The arrogance intervals, which you’ll presumably assemble, have uncertainties related to them. When you draw 100 samples from the identical inhabitants → you get 100 totally different confidence intervals → 95 of them are anticipated to seize the true inhabitants parameter. You might be, as if, throwing confidence intervals on the fastened inhabitants parameter.
The above narrative implies when you draw just one pattern, the chance that the boldness interval captures the true inhabitants parameter (i.e., the fastened goal) is 95%.
With out delving too deep into philosophy, in colloquial English,
The bowl accommodates the apple == The apple is within the bowl
The 2 statements indicate the identical factor as a result of we’re within the land of certainty. Once we imagine that we all know one thing for positive, we don’t make any probabilistic statements. (please don’t ask: do we all know something for positive? 🙏)
Nonetheless, once we are within the land of “some” uncertainty, in statistical English,
We’re 95% assured that the bowl accommodates the apple =/= We’re 95% assured that the apple is within the bowl
I hope this helps. Once more, I recognize your nice feedback on my articles. I hope we proceed this dialogue and assist one another make sense of the complicated world with a bit extra readability.
In the meantime, if you need to learn a few of my earlier posts on the way to try and know the unknown, listed below are some recommendations:

