Understanding and evaluating completely different strategies for conditional causal inference evaluation

A/B checks or randomized managed trials are the gold customary in causal inference. By randomly exposing items to a remedy we guarantee that handled and untreated people are comparable, on common, and any consequence distinction we observe could be attributed to the remedy impact alone.
Nevertheless, usually the remedy and management teams are not completely comparable. This might be because of the truth that randomization was not good or out there. It isn’t at all times doable to randomize a remedy, for moral or sensible causes. Even after we can, generally we should not have sufficient people or items, in order that variations between teams are seizable. This occurs usually, for instance, when randomization will not be finished on the particular person stage, however at a better stage of aggregation, for instance, zip codes, counties, and even states.
In these settings, we are able to nonetheless get well a causal estimate of the remedy impact if we now have sufficient info about people, by making the remedy and management group comparable, ex-post. On this weblog submit, we’re going to introduce and examine completely different procedures to estimate causal results in presence of imbalances between remedy and management teams which can be totally observable. Particularly, we’re going to analyze weighting, matching, and regression procedures.
Assume we had a weblog on statistics and causal inference. To enhance person expertise, we’re contemplating releasing a darkish mode, and we want to perceive whether or not this new characteristic will increase the time customers spend on our weblog.

We’re not a complicated firm, subsequently we do not run an A/B check however we merely launch the darkish mode and we observe whether or not customers choose it or not and the time they spend on the weblog. We all know that there is likely to be choice: customers that want the darkish mode might have completely different studying preferences and this would possibly complicate our causal evaluation.
We will signify the information producing course of with the next Directed Acyclic Graph (DAG).

We generate the simulated knowledge utilizing the information producing course of dgp_darkmode() from src.dgp. I additionally import some plotting capabilities and libraries from src.utils.
from src.utils import *
from src.dgp import dgp_darkmodedf = dgp_darkmode().generate_data()
df.head()

We’ve got info on 300 customers for whom we observe whether or not they choose the dark_mode (the remedy), their weekly read_time (the result of curiosity) and a few traits like gender, age and whole hours beforehand spend on the weblog.
We want to estimate the impact of the brand new dark_mode on customers’ read_time. If we have been working an A/B check or randomized management trial, we might simply examine customers with and with out the darkish mode and we might attribute the distinction in common studying time to the dark_mode. Let’s examine what quantity we might get.
np.imply(df.loc[df.dark_mode==True, 'read_time']) - np.imply(df.loc[df.dark_mode==False, 'read_time'])-1.3702904153929154
People that choose the dark_mode spend on common 1.37 hours much less on the weblog, per week. Ought to we conclude that dark_mode is a unhealthy thought? Is that this a causal impact?
We didn’t randomize the dark_mode in order that customers that chosen it won’t be immediately comparable with customers that did not. Can we confirm this concern? Partially. We will solely examine traits that we observe, gender, age and whole hours in our setting. We can’t examine if customers differ alongside different dimensions that we do not observe.
Let’s use the create_table_one perform from Uber’s causalml package deal to supply a covariate stability desk, containing the typical worth of our observable traits, throughout remedy and management teams. Because the identify suggests, this could at all times be the primary desk you current in causal inference evaluation.
from causalml.match import create_table_oneX = ['male', 'age', 'hours']
table1 = create_table_one(df, 'dark_mode', X)
table1

There appears to be some distinction between the remedy (dark_mode) and management group. Particularly, customers that choose the dark_mode are older, have spent fewer hours on the weblog and they’re extra prone to be males.
One other method to visually observe all of the variations directly is with a paired violinplot. The benefit of the paired violinplot is that it permits us to watch the complete distribution of the variable (approximated through kernel density estimation).

The perception of the violinplot may be very comparable: it appears that evidently customers that choose the dark_mode are completely different from customers that do not.
Why will we care?
If we don’t management for the observable traits, we’re unable to estimate the true remedy impact. Briefly, we can’t be sure that the distinction within the consequence, read_time, could be attributed to the remedy, dark_mode, as an alternative of different traits. For instance, it might be that males learn much less and likewise want the dark_mode, subsequently we observe a unfavourable correlation despite the fact that dark_mode has no impact on read_time (and even constructive).
By way of Directed Acyclic Graphs, which means that we now have a number of backdoor paths that we have to block to ensure that our evaluation to be causal.

How will we block backdoor paths? By conditioning the evaluation on these intermediate variables. The conditional evaluation permits us to get well the typical remedy impact of the dark_mode on read_time.

How will we situation the evaluation on gender, age and hours? We’ve got some choices:
- Matching
- Propensity rating weighting
- Regression with management variables
Let’s discover and examine them!
Conditional Evaluation
We assume that for a set of topics i = 1, …, n we noticed a tuple (Dᵢ, Yᵢ, Xᵢ) comprised of
- a remedy project Dᵢ ∈ {0,1} (
dark_mode) - a response Yᵢ ∈ ℝ(
read_time) - a characteristic vector Xᵢ ∈ ℝⁿ (
gender,ageandhours)
Assumption 1: unconfoundedness (or ignorability, or choice on observables)

i.e. conditional on observable traits X, the remedy project D is pretty much as good as random. What we’re successfully assuming is that there aren’t any different traits that we don’t observe that might impression each whether or not a person selects the dark_mode and their read_time. This can be a robust assumption that’s extra prone to be happy the extra particular person traits we observe.
Assumption 2: overlap (or widespread assist)

i.e. no statement is deterministically assigned to the remedy or management group. This can be a extra technical assumption that mainly signifies that for any stage of gender, age or hours, there might exist a person that choose the dark_mode and one that does not. Otherwise from the unconfoundedness assumption, the general assumption is testable.
Matching
The primary and most intuitive methodology to carry out conditional evaluation is matching.
The thought of matching may be very easy. Since we aren’t positive whether or not, for instance, female and male customers are immediately comparable, we do the evaluation inside gender. As a substitute of evaluating read_time throughout dark_mode in the entire pattern, we do it individually for female and male customers.
df_gender = pd.pivot_table(df, values='read_time', index='male', columns='dark_mode', aggfunc=np.imply)
df_gender['diff'] = df_gender[1] - df_gender[0]
df_gender

Now the impact of dark_mode appears reversed: it’s unfavourable for male customers (-0.79) however greater and constructive for feminine customers (+1.38), suggesting a constructive combination impact, 1.38 – 0.79 = 0.59 (assuming an equal proportion of genders)! This signal reversal is a really classical instance of Simpson’s Paradox.
This comparability was simple to carry out for gender, since it’s a binary variable. With a number of variables, doubtlessly steady, matching turns into far more troublesome. One widespread technique is to match customers within the remedy group with probably the most comparable person within the management group, utilizing some type of nearest neighbor algorithm. I will not go into the algorithm particulars right here, however we are able to carry out the matching with the NearestNeighborMatch perform from the causalml package deal.
The NearestNeighborMatch perform generates a brand new dataset the place customers within the remedy group have been matched 1:1 (choice ratio=1) to customers within the management group.
from causalml.match import NearestNeighborMatchpsm = NearestNeighborMatch(exchange=True, ratio=1, random_state=1)
df_matched = psm.match(knowledge=df, treatment_col="dark_mode", score_cols=X)
Are the 2 teams extra comparable now? We will produce a brand new model of the stability desk.
table1_matched = create_table_one(df_matched, "dark_mode", X)
table1_matched
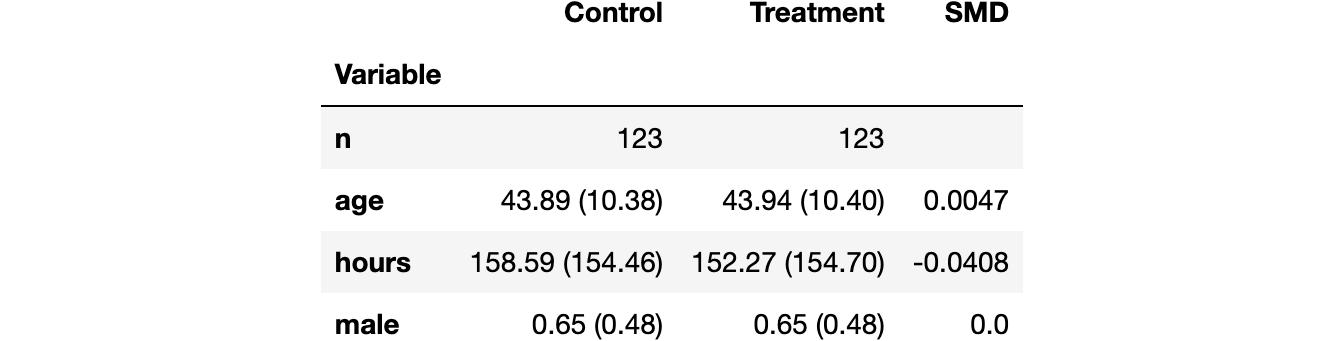
Now the typical variations between the 2 teams have shrunk by at the least a few orders of magnitude. We will visually examine distributional variations with the paired violinplot.
plot_distributions(df_matched, X, "dark_mode")

A well-liked method to visualize pre- and post-matching covariate stability is the stability plot that primarily shows the standardized imply variations earlier than and after matching, for every management variable.
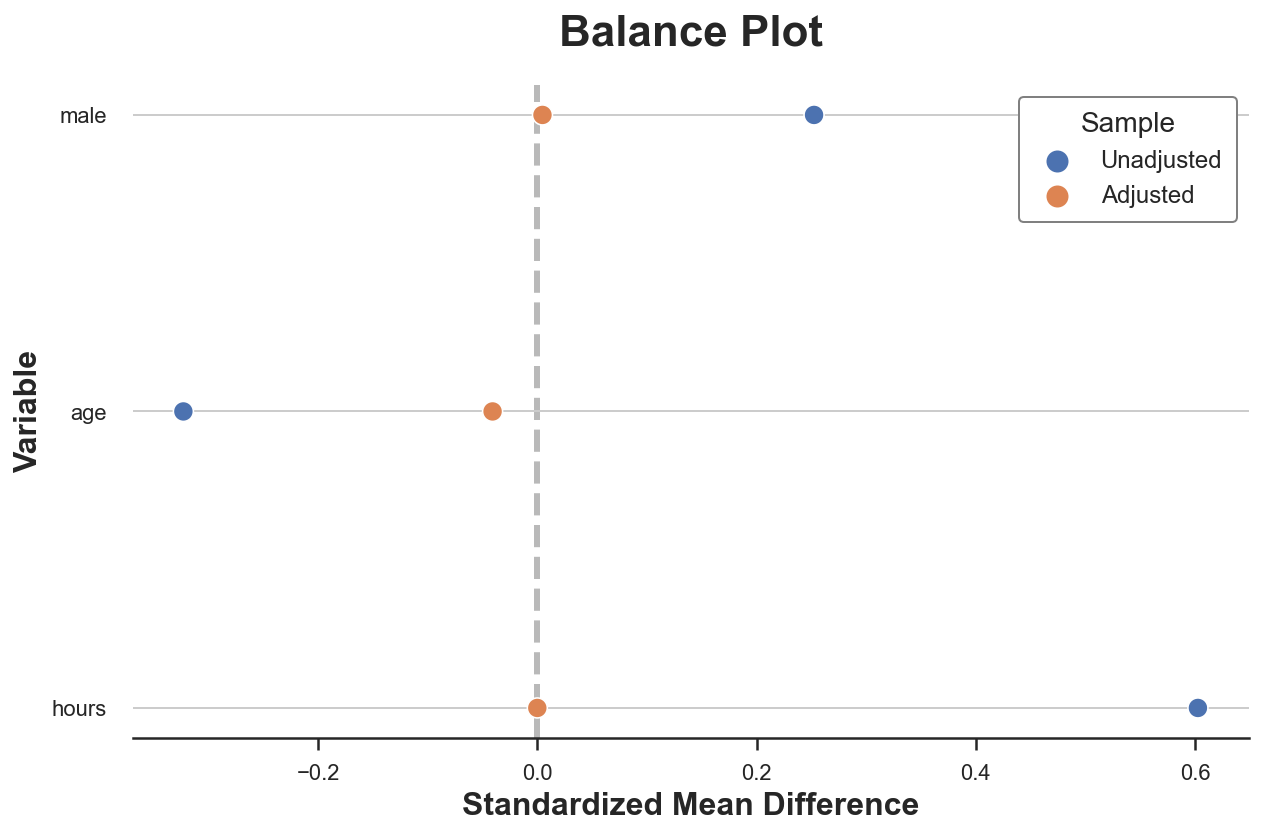
As we are able to see, now all variations in observable traits between the 2 teams are primarily zero. We might additionally examine the distributions utilizing different metrics or check statistics, such because the Kolmogorov-Smirnov check statistic.
How will we estimate the typical remedy impact? We will merely do a distinction in means. An equal approach that mechanically supplies customary errors is to run a linear regression of the result, read_time, on the remedy, dark_mode.
smf.ols("read_time ~ dark_mode", knowledge=df_matched).match().abstract().tables[1]

The impact is now constructive, however not statistically vital.
Propensity Rating
Rosenbaum and Rubin (1983) proved a really highly effective consequence: if the robust ignorability assumption holds, it’s enough to situation the evaluation on the likelihood of remedy, the propensity rating, with a view to have conditional independence.

The place e(Xᵢ) is the likelihood of remedy of particular person i, given the observable traits Xᵢ.

Notice that in an A/B check the propensity rating is fixed throughout people.
The consequence from Rosenbaum and Rubin (1983) is extremely highly effective and sensible, because the propensity rating is a one-dimensional variable, whereas the management variable X is likely to be very high-dimensional.
Beneath the unconfoundedness assumption launched above, we are able to rewrite the typical remedy impact as
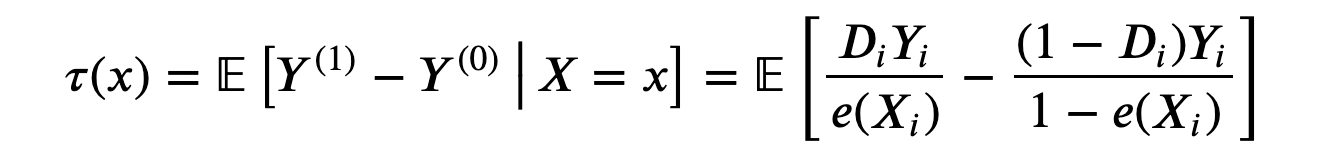
Notice that this formulation of the typical remedy impact doesn’t depend upon the potential outcomes Yᵢ⁽¹⁾ and Yᵢ⁽⁰⁾, however solely on the noticed outcomes Yᵢ.
This formulation of the typical remedy impact implies the Inverse Propensity Weighted (IPW) estimator which is an unbiased estimator for the typical remedy impact τ.
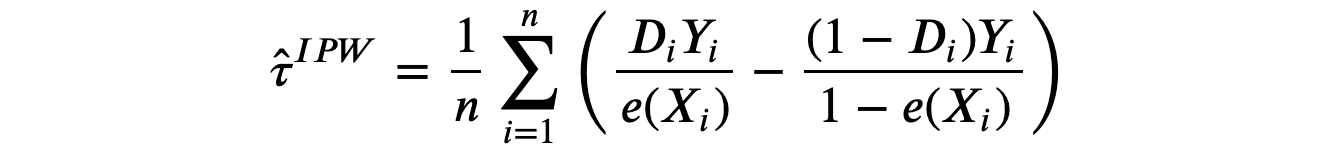
This estimator is unfeasible since we don’t observe the propensity scores e(Xᵢ). Nevertheless, we are able to estimate them. Truly, Imbens, Hirano, Ridder (2003) present that you just ought to use the estimated propensity scores even in case you knew the true values (for instance as a result of the sampling process). The thought is that if the estimated propensity scores are completely different from the true ones, this may be informative within the estimation.
There are a number of doable methods to estimate a likelihood, the only and commonest one being logistic regression.
df["pscore"] = smf.logit("np.rint(dark_mode) ~ male + age + hours", knowledge=df).match(disp=False).predict()
An essential examine to carry out after estimating propensity scores is plotting them, throughout the remedy and management teams. To begin with, we are able to then observe whether or not the 2 teams are balanced or not, relying on how shut the 2 distributions are. Furthermore, we are able to additionally examine how seemingly it’s that the overlap assumption is happy. Ideally, each distributions ought to span the identical interval.
sns.histplot(knowledge=df, x='pscore', hue='dark_mode', bins=30, stat='density', common_norm=False).
set(ylabel="", title="Distribution of Propensity Scores");

As anticipated, the distribution of propensity scores between the remedy and management teams is considerably completely different, suggesting that the 2 teams are hardly comparable. Nevertheless, there’s a vital overlap within the assist of the distributions, suggesting that the overlap assumption is prone to be happy.
How will we estimate the typical remedy impact?
As soon as we now have computed the propensity scores, we simply have to re-weight observations by their respective propensity rating. We will then both compute a distinction between the weighted read_time averages, or run a weighted regression of read_time on dark_mode.
w = 1 / (df["pscore"] * df["dark_mode"] + (1-df["pscore"]) * (1-df["dark_mode"]))
smf.wls("read_time ~ dark_mode", weights=w, knowledge=df).match().abstract().tables[1]

The impact of the dark_mode is now constructive and statistically vital, on the 5% stage!
Regression with Management Variables
The final methodology we’re going to assessment as we speak is linear regression with management variables. This estimator is extraordinarily simple to implement since we simply want so as to add the person traits — gender, age and hours – to the regression of read_time on dark_mode.
smf.ols("read_time ~ dark_mode + male + age + hours", knowledge=df).match().abstract().tables[1]

The typical remedy impact is once more constructive and statistically vital on the 1% stage!
Regression appears a lot much less clear with respect to the earlier strategies. How does it examine?
There’s a tight connection between the IPW estimator and linear regression with covariates. That is notably evident when we now have a one-dimensional, discrete covariate X.
On this case, the estimand of IPW (i.e. the amount that IPW estimates) is given by

The IPW estimand is a weighted common of the remedy results τₓ, the place the weights are given by the remedy possibilities.
The estimand of linear regression with management variables is
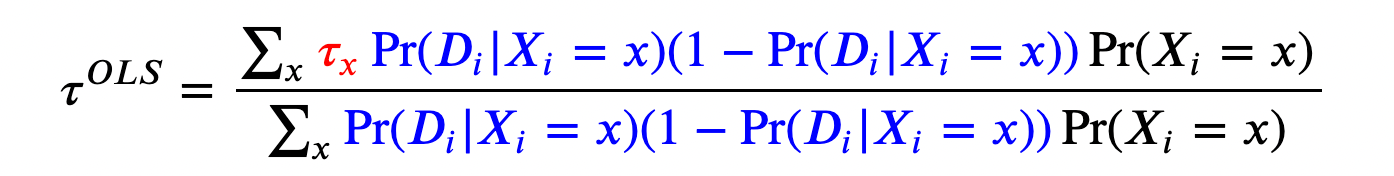
The OLS estimand is a weighted common of the remedy results τₓ, the place the weights are given by the variances of the remedy possibilities. Which means that linear regression is a weighted estimator, that offers extra weight to observations which have traits for which we observe extra remedy variability. Since a binary random variable has the best variance when its anticipated worth is 0.5, OLS offers probably the most weight to observations which have traits for which we observe a 50/50 cut up between the remedy and management group. However, if for some traits we solely observe handled or untreated people, these observations are going to obtain zero weight. I like to recommend Chapter 3 of Angrist and Pischke (2009) for extra particulars.
On this weblog submit, we now have seen the best way to carry out conditional evaluation utilizing completely different approaches. Matching immediately matches most comparable items within the remedy and management teams. Weighting merely assigns completely different weights to completely different observations relying on their likelihood of receiving the remedy. Regression as an alternative weights observations relying on the conditional remedy variances, giving extra weight to observations which have traits widespread to each the remedy and management group.
These procedures are extraordinarily useful as a result of they’ll both permit us to estimate causal results from (very wealthy) observational knowledge or appropriate experimental estimates when randomization was not good or we now have a small pattern.
Final however not least, if you wish to know extra, I strongly suggest this video lecture on propensity scores from Paul Goldsmith-Pinkham which is freely out there on-line.
The entire course is a gem and it’s an unimaginable privilege to have such high-quality materials out there on-line without cost!
References
[1] P. Rosenbaum, D. Rubin, The central function of the propensity rating in observational research for causal results (1983), Biometrika.
[2] G. Imbens, Ok. Hirano, G. Ridder, Environment friendly Estimation of Common Therapy Results Utilizing the Estimated Propensity Rating (2003), Econometrica.
[3] J. Angrist, J. S. Pischke, Principally innocent econometrics: An Empiricist’s Companion (2009), Princeton College Press.
Associated Articles
Code
Yow will discover the unique Jupyter Pocket book right here:
Thanks for studying!
I actually respect it! 
Additionally, a small disclaimer: I write to study so errors are the norm, despite the fact that I attempt my greatest. Please, whenever you spot them, let me know. I additionally respect recommendations on new subjects!