How would you construct a machine studying algorithm to unravel the next kinds of issues?
- Predict which medal athletes will win within the olympics.
- Predict how a shoe will match a foot (too small, excellent, too massive).
- Predict what number of stars a critic will charge a film.
In case you attain into your typical toolkit, you’ll most likely both attain for regression or multiclass classification. For regression, possibly you deal with the variety of stars (1-5) within the film critic query as your goal, and also you practice a mannequin utilizing imply squared error as your loss operate. For multiclass classification, possibly you deal with bronze, silver, and gold medals as three separate courses and practice a mannequin with cross entropy loss.
Whereas these approaches can work, they ignore a elementary side of the prediction targets within the proposed issues: the targets have ordinal relationships to one another. There’s a bigger distinction between bronze and gold than silver and gold. Equally, from the standpoint of the mannequin that we want to construct, our fallacious predictions ought to have ordinal relationships. If we predict {that a} piece of clothes might be too massive on a buyer and we get our prediction fallacious, then it’s extra probably that the clothes match the shopper than that we obtained issues totally fallacious sucht that the clothes was too small.
This class of issues known as ordinal regression. Whereas generally seen in business, the tooling and training round utilizing these fashions is considerably missing. As effectively, the instruments that do exist are reasonably rigid in that one is proscribed within the kinds of fashions and methods that can be utilized. I’ve a considerably idealistic purpose of taking the entire bespoke machine studying strategies for which individuals used to unravel by way of linear fashions and manually calculated gradients and as an alternative rewrite these fashions utilizing a deep studying framework with customized loss capabilities optimizable by stochastic gradient descent (SGD). This may enable folks to maneuver past linear fashions (to, say, deep neural networks) and luxuriate in the entire advantages of SGD (ADAM, batch norm, scale, and so on…). As effectively, I’d like to do that all in a scikit-learn-compatible manner as a result of I simply love their API.
As an instance my level, let’s have a look at the one scikit-learn-compatible library I might discover that matches ordinal regression fashions, mord. Don’t get me fallacious, this library is nice and fast and created by a verifiable skilled in ordinal regression fashions. Nevertheless, the entire fashions obtainable are linear fashions with L2 regularization. What if I wish to throw a deep studying mannequin in there? What if I wish to induce sparsity with LASSO? I must manually calculate the target capabilities and related gradients and create a model new class within the library. If I can as an alternative suitably outline a loss operate suitable with ordinal regression, then I can use any of the deep studying frameworks that use autodifferentiation to optimize no matter mannequin I would like. And I’d like to have the ability to scale this to giant information, which guidelines out the stan and pymc3 implementations.
In order that’s what I did, and I created a small library spacecutter to implement ordinal regression fashions in PyTorch. On this submit, I’ll clarify how ordinal regression works, present how I impemented the mannequin in PyTorch, wrap the mannequin with skorch to show it right into a scikit-learn estimator, after which share some outcomes on a canned dataset.
From Binary to Ordinal Regression
There are a variety of the way to unravel ordinal regression issues, and I’ll solely stroll by one methodology on this submit. I discovered this paper that was referenced in mord to offer an excellent introduction to find out how to remedy these issues. For the approach used on this part, I referenced this paper by the creator of mord, Fabian Pedregosa. Though he didn’t create this system, the referenced papers have been behind paywalls, so I can’t vouch for them.
The primary thought behind ordinal regression is that we discover ways to reduce our prediction house up utilizing cutpoints. However earlier than we get into that, let’s rapidly assessment binary logistic regression the place we have now two goal courses, 0 and 1. Recall that in logistic regression, we have now some linear mannequin $f(mathbf{X}) = mathbf{X} cdot boldsymbol{beta} $ that turns a design matrix $mathbf{X}$ and a vector of coefficients $boldsymbol{beta}$ right into a single quantity that lies someplace between unfavorable and optimistic infinity ($mathbb{R}$). The output of this linear mannequin is then handed by a logistic operate $sigma$ which maps the vary of values between 0 and 1:
$$ sigma(f(mathbf{X})) = frac{1}{1 + e^{-mathbf{X} cdot boldsymbol{beta} }} $$
This operate seems like as follows:
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import numpy as np
plt.ion()
plt.rcParams['figure.figsize'] = (8, 5)
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['axes.labelsize'] = 18
plt.rcParams['legend.fontsize'] = 16
plt.rcParams['xtick.labelsize'] = 14
plt.rcParams['ytick.labelsize'] = 14
num_points = 101
f = np.linspace(-12, 12, num_points)
sigma = lambda f: 1 / (1 + np.exp(-f))
plt.plot(f, sigma(f));
plt.ylabel('$sigma(f)$');
plt.xlabel('$f$');
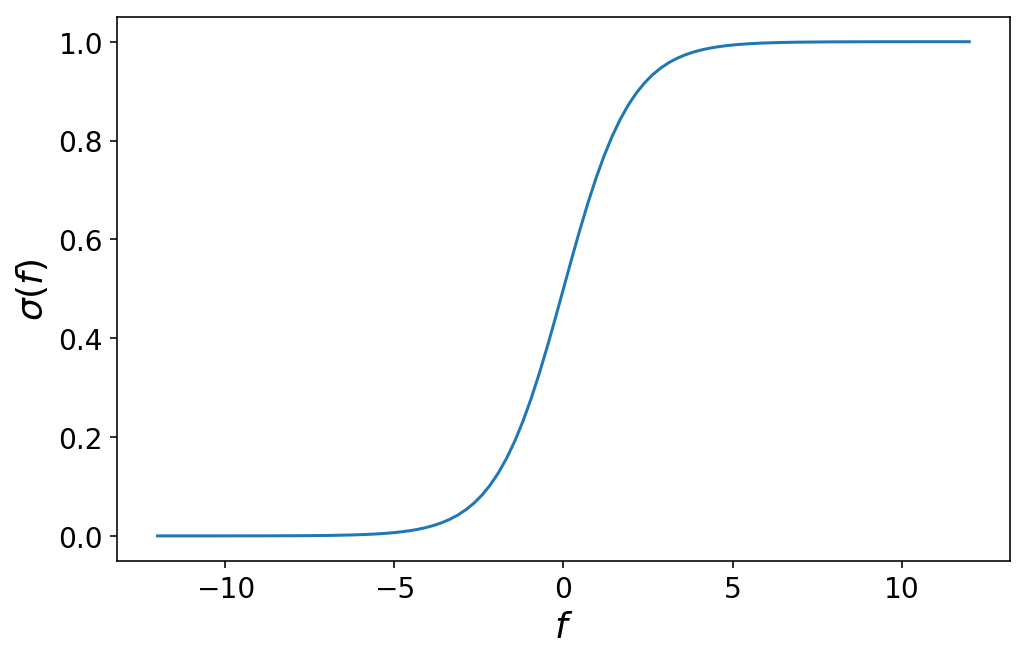
By means of some math, it’s doable to persuade your self that choosing a selected worth of f corresponds to the chance that the remark that produced f belongs to class 1. We’ll write that as
$$P(y = 1) = sigma(f)$$
The chance that the remark belongs to class 0 is
$$
start{aligned}
P(y = 0) & = 1 – P(y = 1) cr
& = 1 – sigma(f)
finish{aligned}
$$
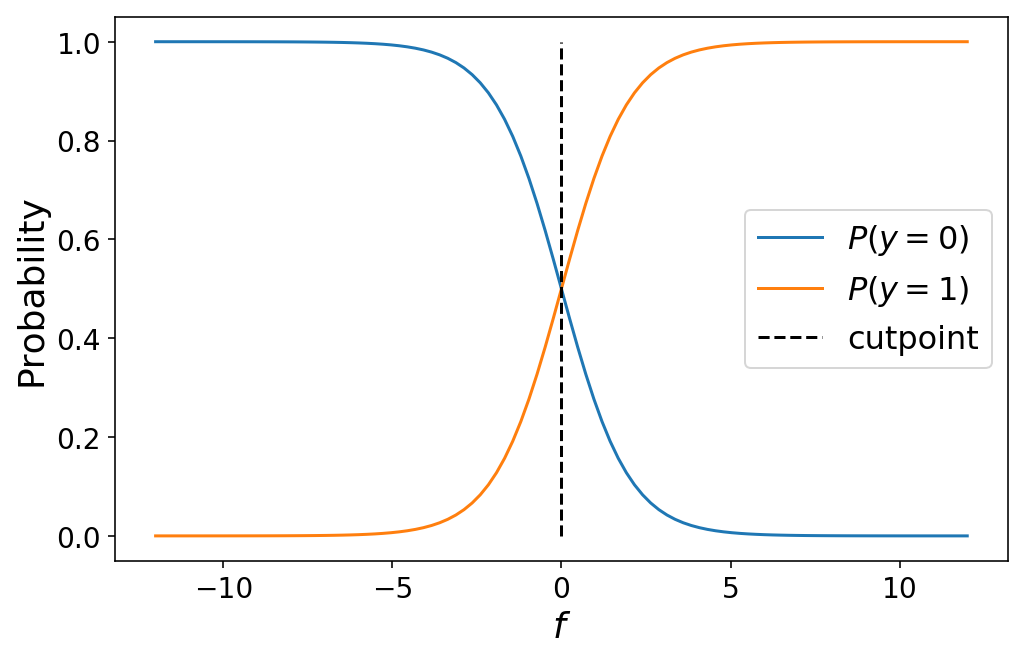
The worth of $f = 0$ is particular in that it marks the precise crossover level the place the remark has a 50% chance of belonging to both class 0 or class 1. Within the language of ordinal regression, we are able to name $f = 0$ a cutpoint which divides our prediction house between class 0 and 1:
plt.plot(f, 1 - sigma(f));
plt.plot(f, sigma(f));
plt.plot((0, 0), (0, 1), 'k--');
plt.legend(['$P(y = 0)$', '$P(y = 1)$', 'cutpoint'])
plt.ylabel('Likelihood');
plt.xlabel('$f$');
Shifting from binary classification to ordinal regression with 3+ courses entails merely defining extra cutpoints to cut up our prediction house into “class chance” house. For $Ok$ courses, we may have $Ok – 1$ cutpoints. The chance that an remark belongs to class $okay$ is given by the cumulative logistic hyperlink operate:
$$
P(y = okay) =
start{circumstances}
sigma(c_0 – f(mathbf{X})),, textual content{if } okay = 0 cr
sigma(c_{okay} – f(mathbf{X})) – sigma(c_{okay – 1} – f(mathbf{X})) ,, textual content{if } 0 < okay < Ok cr
1 – sigma(c_{Ok – 1} – f(mathbf{X})) ,, textual content{if } okay = Ok cr
finish{circumstances}
$$
One factor to notice is that this completely collapses to binary classification within the occasion that we solely have two courses (attempt it out for your self!). The next plot exhibits the category possibilities for a three-class ordinal regression mannequin:
def plot_ordinal_classes(f, cutpoints):
num_classes = len(cutpoints) + 1
labels = []
for idx in vary(num_classes):
if idx == 0:
plt.plot(f, sigma(cutpoints[0] - f));
elif idx == num_classes - 1:
plt.plot(f, 1 - sigma(cutpoints[-1] - f));
else:
plt.plot(f, sigma(cutpoints[idx] - f) - sigma(cutpoints[idx - 1] - f));
labels.append(f'$P(y = {idx})$')
for c in cutpoints:
plt.plot((c, c), (0, 1), 'k--')
labels.append('cutpoints')
plt.legend(labels);
plt.ylabel('Likelihood');
plt.xlabel('$f$');
cutpoints = [-2, 2]
plot_ordinal_classes(f, cutpoints)
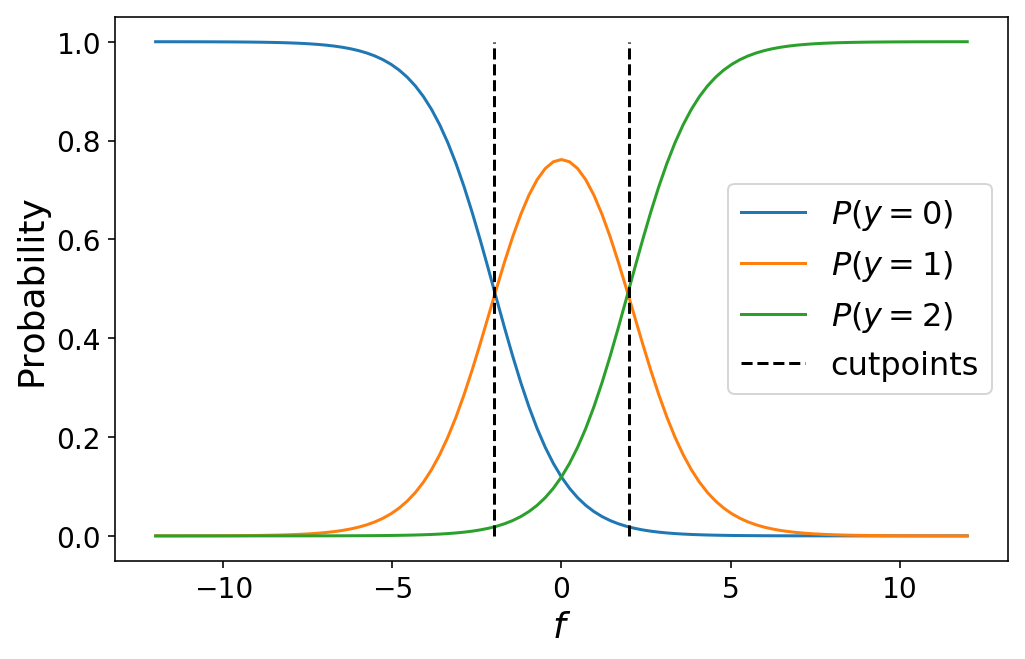
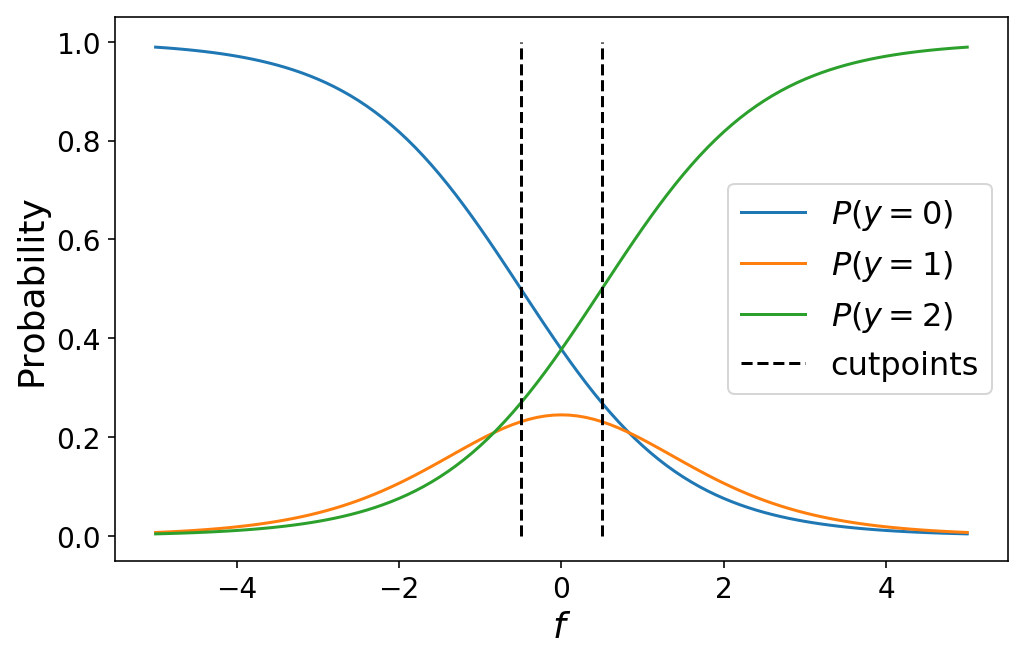
Whereas I outlined the cutpoints by hand above, in apply we might be taught the optimum values for the cutpoints as a part of our machine studying drawback (which we’ll discuss within the subsequent part). Various the cutpoints varies the category possibilities. This could typically result in unintuitive outcomes when the cutpoints are shut collectively similar to a selected class by no means being the most certainly class for any worth of $f$.
plot_ordinal_classes(np.linspace(-5, 5, 101), [-0.5, 0.5])
The next animation exhibits the category possibilities for a 5-class mannequin as we range the cutpoints.
Studying Ordinal Regression
Now that we have now our mannequin that predicts ordinal class possibilities, it’s solely a small step to studying a mannequin. We merely have to outline a loss operate and decrease. Our loss operate would be the unfavorable log chance which corresponds to the unfavorable log of the category chance that we predict for whichever class is the “true” class for a selected remark. In pseudocode, think about that we have now three courses and a prediction y_pred = [0.25, 0.5, 0.25] akin to the expected class chance for every of the three courses. If y_true = 1, then our loss is -log(y_pred[1]). That is simple sufficient to outline in PyTorch, after which all we have now to do is optimize each our mannequin and our cutpoints by way of Stochastic Gradient Descent (SGD).
One wrinkle is that our cutpoints must be in ascending order. That’s, cutpoint[0] < cutpoint[1] < ... cutpoint[K-1]. It is a constraint on our optimization drawback which isn’t simply dealt with by SGD. My soiled hack is to clip the cutpoint values after every gradient replace to make sure that they’re at all times in ascending order. With extra time, I’d prefer to implement a extra correct answer.
spacecutter
Let’s recap on how we practice ordinal regression fashions:
- We create some mannequin that generates a single, scalar prediction.
- Use the cumulative logistic hyperlink operate to map that scalar to ordinal class possibilities.
- Outline and decrease the unfavorable log chance loss akin to the predictions.
- Be sure that the
cutpointsstay in ascending order.
Now, let’s stroll by how to do that in spacecutter. We’ll use a wine high quality dataset from the UCI repository by which every remark is a wine rated on a scale from 1-10. We begin by downloading the dataset, inspecting a number of the options, and performing some fundamental preprocessing of the options utilizing the brand new ColumnTransformer in scikit-learn.
import warnings
import pandas as pd
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_absolute_error, accuracy_score, make_scorer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PowerTransformer, FunctionTransformer
from skorch.callbacks import Callback, ProgressBar
from skorch.internet import NeuralNet
import torch
from torch import nn
warnings.simplefilter('ignore')
# Obtain the dataset
# !wget "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
wine = pd.read_csv('winequality-red.csv', sep=';')
wine.head()
| mounted acidity | risky acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | whole sulfur dioxide | density | pH | sulphates | alcohol | high quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
| 1 | 7.8 | 0.88 | 0.00 | 2.6 | 0.098 | 25.0 | 67.0 | 0.9968 | 3.20 | 0.68 | 9.8 | 5 |
| 2 | 7.8 | 0.76 | 0.04 | 2.3 | 0.092 | 15.0 | 54.0 | 0.9970 | 3.26 | 0.65 | 9.8 | 5 |
| 3 | 11.2 | 0.28 | 0.56 | 1.9 | 0.075 | 17.0 | 60.0 | 0.9980 | 3.16 | 0.58 | 9.8 | 6 |
| 4 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
Plainly everyone charges the wine high quality someplace between 3 and eight. We’ll map these to courses 0-5.
y = wine.pop('high quality')
(y.value_counts()
.sort_index()
.plot(variety='bar'));
plt.ylabel('Counts');
plt.xlabel('High quality');
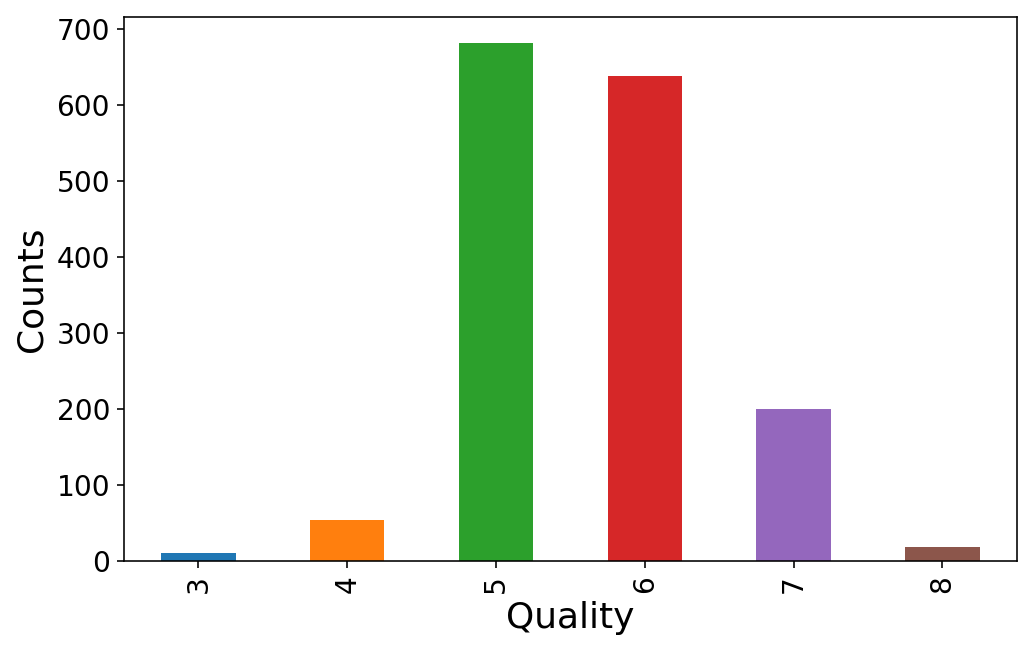
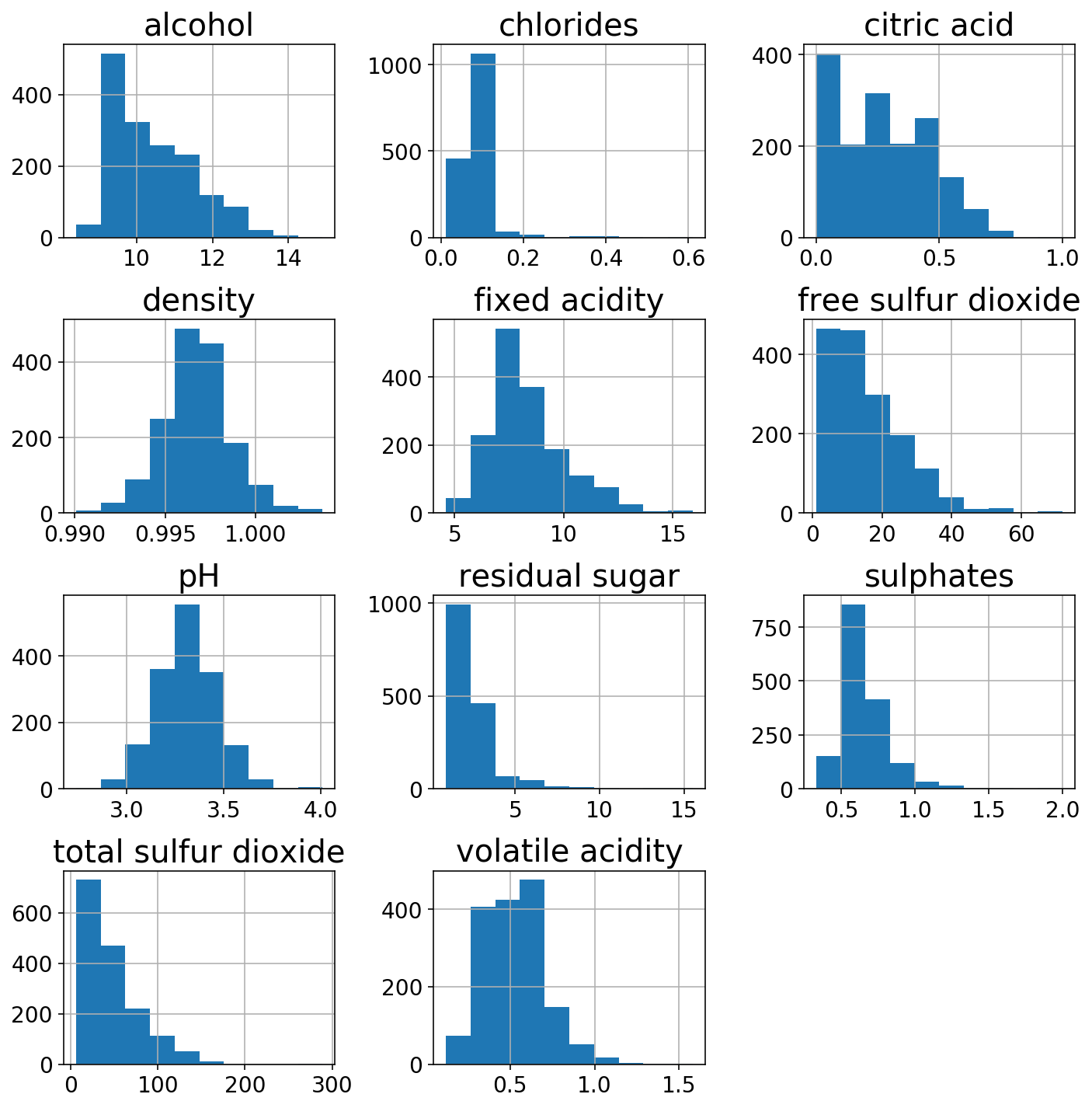
We’ll take a look at the distributions of the 11 totally different options.
wine.hist(figsize=(10, 10));
plt.tight_layout();
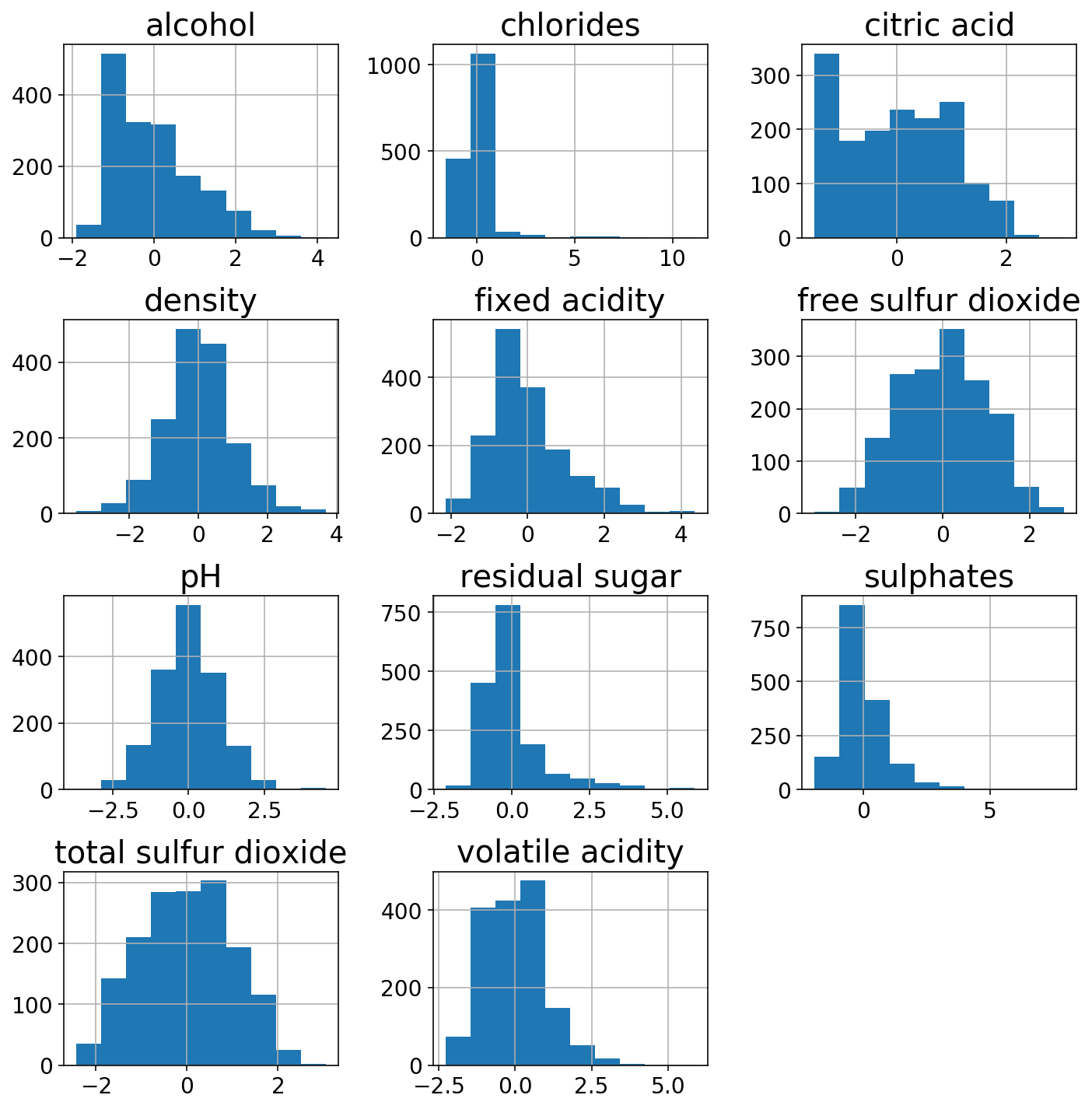
Simply to indicate off the facility of the ColumnTransformer, I’ll use a StandardScaler on the extra gaussian-like columns and a PowerTransformer on the opposite ones. The remodeled options look a bit extra regular.
gaussian_columns = ['alcohol', 'chlorides', 'fixed acidity',
'density',
'pH', 'sulphates', 'volatile acidity']
power_columns = ['citric acid', 'free sulfur dioxide', 'residual sugar',
'total sulfur dioxide']
column_transformer = ColumnTransformer([
('gaussian', StandardScaler(), gaussian_columns),
('power', PowerTransformer(), power_columns)
])
X_trans = column_transformer.fit_transform(wine)
(pd.DataFrame(X_trans,
columns=gaussian_columns + power_columns)
.hist(figsize=(10, 10)));
plt.tight_layout();
y = y.values.astype(np.lengthy).reshape(-1, 1)
# Map y from (3-8) to (0-5)
y -= y.min()
X = wine
(X_train, X_test,
y_train, y_test) = train_test_split(X, y, test_size=0.33,
stratify=y, random_state=666)
Cool, now that we have now an X and y and a preprocessing transformer, we are able to get to coaching the mannequin. Do not forget that step one for ordinal regression is a mannequin that predicts a single scalar worth. I’ll create a easy two-layer neural community in PyTorch for this function.
num_features = len(gaussian_columns + power_columns)
predictor = nn.Sequential(
nn.Linear(num_features, num_features),
nn.ReLU(inplace=True),
nn.Linear(num_features, num_features),
nn.ReLU(inplace=True),
nn.Linear(num_features, 1, bias=False)
)
With spacecutter, we are able to wrap this predictor with the OrdinalLogisticModel which can create cutpoints and go the predictor output by the cumulative logistic hyperlink operate
from spacecutter.fashions import OrdinalLogisticModel
num_classes = len(np.distinctive(y))
mannequin = OrdinalLogisticModel(predictor, num_classes)
X_tensor = torch.as_tensor(X_train.values.astype(np.float32))
predictor_output = predictor(X_tensor).detach()
model_output = mannequin(X_tensor).detach()
print(predictor_output)
print(model_output)
tensor([[-4.9971],
[-1.3892],
[-1.9079],
...,
[-3.1603],
[-5.7689],
[-5.1477]])
tensor([[0.9239, 0.0467, 0.0184, 0.0069, 0.0026, 0.0015],
[0.2477, 0.2246, 0.2364, 0.1599, 0.0786, 0.0527],
[0.3562, 0.2444, 0.2029, 0.1140, 0.0505, 0.0320],
...,
[0.6593, 0.1809, 0.0944, 0.0403, 0.0157, 0.0094],
[0.9633, 0.0228, 0.0087, 0.0032, 0.0012, 0.0007],
[0.9339, 0.0407, 0.0159, 0.0060, 0.0022, 0.0013]])
To coach this mannequin, we’ll use skorch which wraps our mannequin and makes it suitable as a scikit-learn estimator. Crucially, we should go within the CumulativeLinkLoss loss module from spacecutter. Moreover, we use a customized spacecutter callback AscensionCallback which maintains the ascending order of the cutpoints.
from spacecutter.losses import CumulativeLinkLoss
from spacecutter.callbacks import AscensionCallback
skorch_model = NeuralNet(
module=OrdinalLogisticModel,
module__predictor=predictor,
module__num_classes=num_classes,
criterion=CumulativeLinkLoss,
max_epochs=100,
optimizer_type=torch.optim.Adam,
optimizer__weight_decay=0.0,
lr=0.1,
gadget='cpu',
callbacks=[
('ascension', AscensionCallback()),
],
train_split=None,
verbose=0,
)
The final step is to package deal every part up right into a scikit-learn Pipeline. Word: I’ve so as to add a small transformer to ensure that the matrices are floats (and never doubles) earlier than they’re handed into the skorch mannequin.
def to_float(x):
return x.astype(np.float32)
pipeline = Pipeline([
('column', column_transformer),
('caster', FunctionTransformer(to_float)),
('net', skorch_model)
])
Let’s use imply absolute error as our scoring critera and do a grid search throughout variety of epochs, studying charge, and weight decay (aka ~L2 regularization).
def mae_scorer(y_true, y_pred):
return mean_absolute_error(y_true, y_pred.argmax(axis=1))
scoring = make_scorer(mae_scorer,
greater_is_better=False,
needs_proba=True)
param_grid = {
'net__max_epochs': np.logspace(1, 3, 5).astype(int),
'net__lr': np.logspace(-4, -1, 5),
'net__optimizer__weight_decay': np.logspace(-6, -2, 4)
}
sc_grid_search = GridSearchCV(
pipeline, param_grid, scoring=scoring,
n_jobs=None, cv=5, verbose=1
)
sc_grid_search.match(X_train, y_train)
Becoming 5 folds for every of 100 candidates, totalling 500 matches
[Parallel(n_jobs=1)]: Utilizing backend SequentialBackend with 1 concurrent employees.
[Parallel(n_jobs=1)]: Carried out 500 out of 500 | elapsed: 92.0min completed
GridSearchCV(cv=5, error_score="raise-deprecating",
estimator=Pipeline(reminiscence=None,
steps=[('column', ColumnTransformer(n_jobs=None, remainder="drop", sparse_threshold=0.3,
transformer_weights=None,
transformers=[('gaussian', StandardScaler(copy=True, with_mean=True, with_std=True), ['alcohol', 'chlorides', 'fixed acidity', 'density', 'pH', 'sulphates', 'volatile ...as=True)
(3): ReLU(inplace)
(4): Linear(in_features=11, out_features=1, bias=False)
),
))]),
fit_params=None, iid='warn', n_jobs=None,
param_grid={'net__max_epochs': array([ 10, 31, 100, 316, 1000]), 'net__lr': array([0.0001 , 0.00056, 0.00316, 0.01778, 0.1 ]), 'net__optimizer__weight_decay': array([1.00000e-06, 2.15443e-05, 4.64159e-04, 1.00000e-02])},
pre_dispatch="2*n_jobs", refit=True, return_train_score="warn",
scoring=make_scorer(mae_scorer, greater_is_better=False, needs_proba=True),
verbose=1)
Now that we’re completed our search (86 minutes later…), let’s examine the outcomes.
We are able to see that the cutpoints are fairly separated and in ascending order.
cutpoints = (sc_grid_search
.best_estimator_
.named_steps['net']
.module_
.hyperlink
.cutpoints
.detach())
print(f"Cutpoints: {cutpoints}")
Cutpoints: tensor([-3.3575, -2.6696, -0.1757, 1.9482, 3.6145])
The accuracy is respectable for a multiclass mannequin, and we are able to see that we’re off in our score prediction by lower than 0.5 on common.
y_pred = sc_grid_search.predict_proba(X_test).argmax(axis=1)
print(f'Accuracy = {accuracy_score(y_test.squeeze(), y_pred):1.4f}')
print(f'MAE = {mean_absolute_error(y_test.squeeze(), y_pred):1.4f}')
Accuracy = 0.6250
MAE = 0.3958
bins = np.arange(6)
plt.hist(y_test, bins=bins, alpha=0.5);
plt.hist(y_pred, bins=bins, alpha=0.5);
plt.legend(['y_true', 'y_pred']);
plt.ylabel('Counts');
plt.xlabel('Ordinal Class');
plt.title('spacecutter Class Distributions');
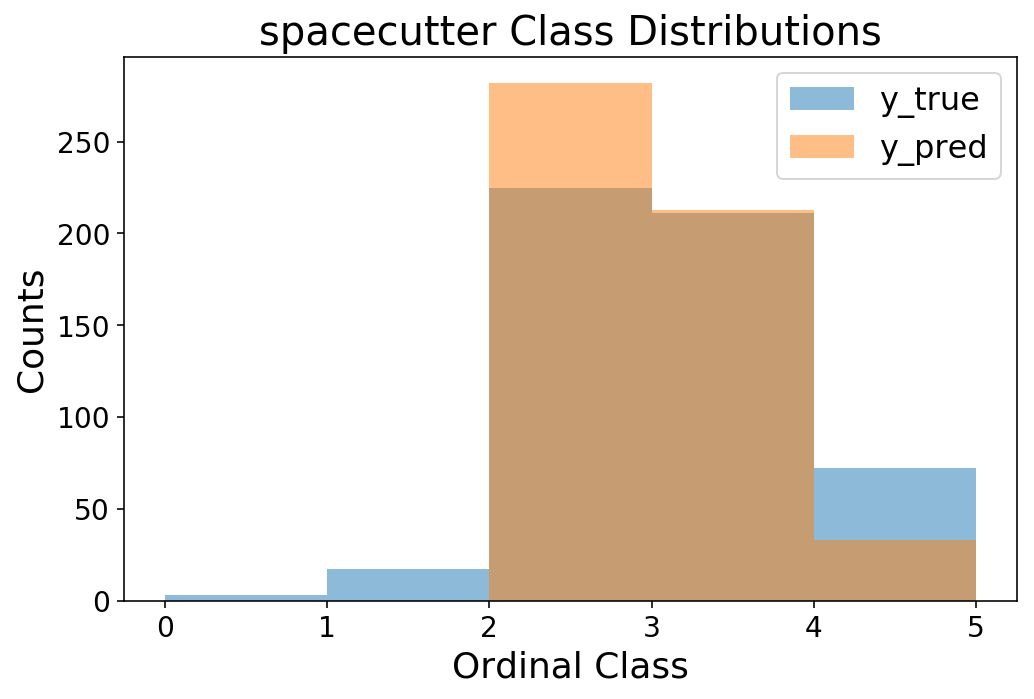
Lastly, let’s do a fast test of how this compares to mord.
from mord.threshold_based import LogisticAT
pipeline = Pipeline([
('column', column_transformer),
('caster', FunctionTransformer(to_float)),
('model', LogisticAT())
])
param_grid = {
'model__max_iter': np.logspace(3, 5, 5).astype(int),
'model__alpha': np.logspace(0, 4, 5)
}
mord_grid_search = GridSearchCV(
pipeline, param_grid, scoring=scoring,
n_jobs=None, cv=5, verbose=1
)
mord_grid_search.match(X_train, y_train)
Becoming 5 folds for every of 25 candidates, totalling 125 matches
[Parallel(n_jobs=1)]: Utilizing backend SequentialBackend with 1 concurrent employees.
[Parallel(n_jobs=1)]: Carried out 125 out of 125 | elapsed: 13.2s completed
GridSearchCV(cv=5, error_score="raise-deprecating",
estimator=Pipeline(reminiscence=None,
steps=[('column', ColumnTransformer(n_jobs=None, remainder="drop", sparse_threshold=0.3,
transformer_weights=None,
transformers=[('gaussian', StandardScaler(copy=True, with_mean=True, with_std=True), ['alcohol', 'chlorides', 'fixed acidity', 'density', 'pH', 'sulphates', 'volatile ...'deprecated',
validate=None)), ('model', LogisticAT(alpha=1.0, max_iter=1000, verbose=0))]),
fit_params=None, iid='warn', n_jobs=None,
param_grid={'model__max_iter': array([ 1000, 3162, 10000, 31622, 100000]), 'model__alpha': array([1.e+00, 1.e+01, 1.e+02, 1.e+03, 1.e+04])},
pre_dispatch="2*n_jobs", refit=True, return_train_score="warn",
scoring=make_scorer(mae_scorer, greater_is_better=False, needs_proba=True),
verbose=1)
cutpoints = (mord_grid_search
.best_estimator_
.named_steps['model']
.theta_)
print(f"Cutpoints: {cutpoints}")
Cutpoints: [-5.80087138 -3.88733054 -0.238343 2.47900366 5.45252331]
y_pred = mord_grid_search.predict(X_test)
print(f'accuracy = {accuracy_score(y_test.squeeze(), y_pred):1.3f}')
print(f'MSE = {mean_absolute_error(y_test.squeeze(), y_pred):1.3f}')
accuracy = 0.612
MSE = 0.415
bins = np.arange(6)
plt.hist(y_test, bins=bins, alpha=0.5);
plt.hist(y_pred, bins=bins, alpha=0.5);
plt.legend(['y_true', 'y_pred']);
plt.ylabel('Counts');
plt.xlabel('Ordinal Class');
plt.title('mord Class Distributions');
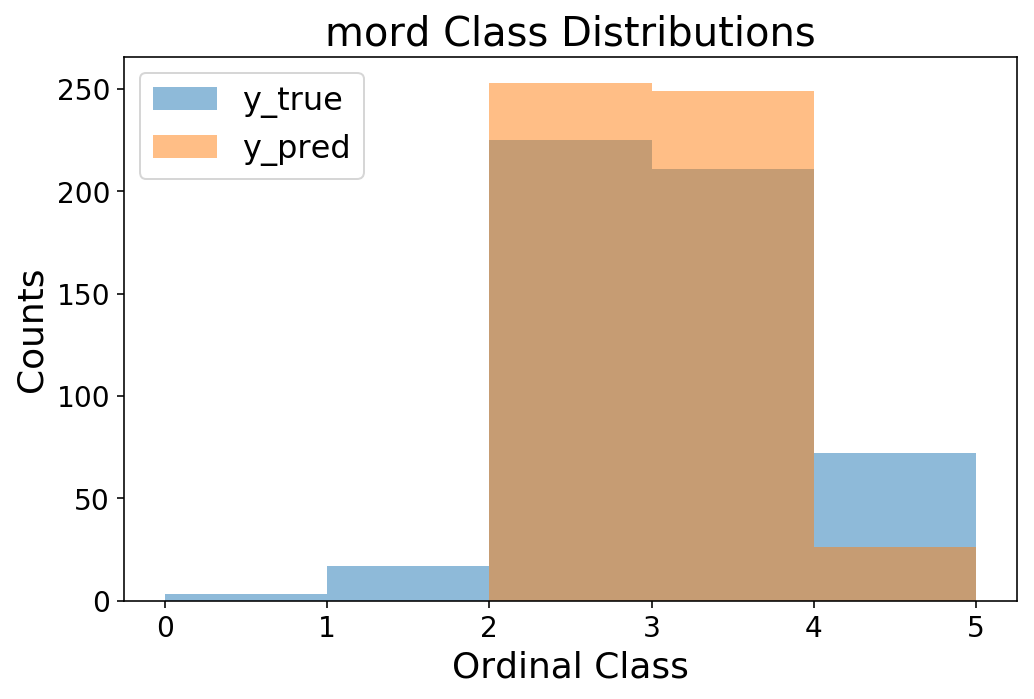
It seems that the outcomes are fairly corresponding to spacecutter! Maybe that is shocking, however we’re coping with small information and few options, so I might not anticipate a neural internet to be significantly helpful. However, it’s an excellent sanity test that we’re doing in addition to a traditional linear mannequin. Now, it’s as much as you to take spacecutter for a spin and take a look at scaling it as much as thousands and thousands of observations 🙂

